简单易懂的整数规划割平面法求解方法

视频-4．2．3整数规划问题求解-3-割平面法

割平面法是1958年由美国学者高莫利提出的求解全整数规划的一种比较简单的方法,其思想与分枝定界法大致相同,都是先求松弛问题的最优解。如果最优解为整数解,则停止计算。如果最优解不是整数解,可用两种方法求解:①分枝定界法是用两个垂直于坐标轴的平行平面xk＝[bk]和xk＝[bk]＋1将原可行域R分成两个可行域R1和R2,并将两个平行平面之间的不含有整数解的那一部分可行域去掉,以缩小可行域。②割平面法是用一张平面(不一定垂直于某个坐标轴)将含有最优解的点但不含任何整数可行解的那一部分可行域切割掉,通过在原整数规划问题的基础上增加适当的线性不等式约束来实现,该线性不等式约束称为切割不等式,当切割不等式取等号时,叫作割平面。然后继续求解这个新的整数规划问题,在这个新的整数规划问题的基础上增加适当的线性不等式约束,直至求得最优整数解为止。需要指出的是,割平面约束可能不是一次就可以找到的。

【例4-12】用割平面法求解下面整数规划问题。

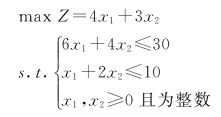
解:

①求解松弛问题。

用单纯形法求解,结果如表4-9所示。

表4-9

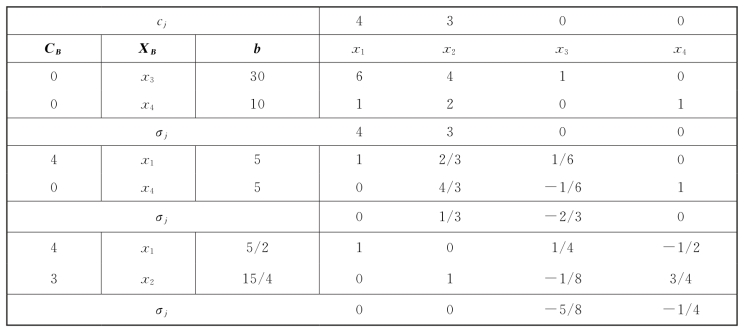
松弛问题最优解为:X∗＝(5/2,15/4,0,0)T,Z∗＝85/4。

②寻找割平面约束。

在最终单纯形表中找到任意一个约束条件,如“x1＋0x2＋(1/4)x3－(1/2)x4＝5/2”,将此约束等式划分为整数和非整数部分,转化过程如下:

x1＋(1/4)x3＋(－1＋1/2)x4＝2＋1/2

x1－x4－2＝1/2－(x3/4＋x4/2)(www.xing528.com)

思考:等式左端在什么条件下有可能为整数?

当等式右端的x3/4＋x4/2取值分别是1/2,(0,1/2)和(1/2,∞)时,等式左端的取值范围分别为“＝0”“＞0”和“＜0”,如模型(4-8)和(4－9)所示。

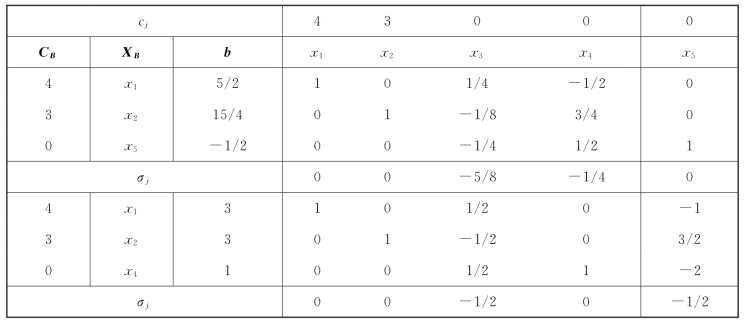
模型(4-8)左端若为整数,则需1/2－(x3/4＋x4/2)≤0,即－x3/4－x4/2≤－1/2,标准化后变为－x3/4－x4/2＋x5＝－1/2,这就是割平面约束。将割平面约束添加到最终单纯形表中,继续求解,过程如表4-10所示,可知该整数规划问题最优解为:X∗＝(3,3,0,1,0)T,Z∗＝21。

表4-10

割平面法求解步骤总结:

①用单纯形法求解松弛问题;

②在松弛问题最终单纯形表中任选一约束条件,构造新的约束条件(割平面约束);

③将新的约束条件加入最终单纯形表中,直至求得最优整数解。

对于本题,割平面约束“－x3/4－x4/2≤－1/2”,可变形为“x3＋2x4≥2”,再将松弛问题原约束“6x1＋4x2＋x3＝30”和“x1＋2x2＋x4＝10”代入“x3＋2x4≥2”中,可得“x1＋x2≤6”(割平面约束),因此原整数规划问题可转化为模型(4-10)。

使用图解法对模型(4-10)求解,结果如图4-13所示。可见,通过构造一系列平面来切割不含有任何整数可行解的部分,将得到一个新的可行域,顶点对应最优整数解。

图4-13