使用分枝定界法求解整数规划问题

视频-4．2．2整数规划问题求解-2-分枝定界法

分枝定界法(Branch and Bound)是求解整数规划问题的常用方法。这种方法不但可以求解纯整数规划问题,还可以求解混合整数规划问题。用分枝定界法(分支定界法)求解整数规划问题的基本思路是,在松弛问题的可行域中寻找使目标函数值达到最优的整数解,这种思路依据下面的定理:

定理:对于某一求max(或min)的整数规划问题,其目标函数最优值不超过(低于)其松弛问题的目标函数最优值。

【例4-10】用分枝定界法求解【例4-1】的整数规划问题模型。

解:

第一步,第一次定界。不考虑整数限制,求出整数规划问题对应松弛问题的最优解,若符合整数要求,则是整数规划问题的最优解,计算结束。否则进行第二步,同时将松弛问题最优解所对应的目标函数值作为整数规划问题的最优目标函数的上界,因变量取值非负,因此将零作为下界。

第二步,第一次分枝。对于松弛问题最优解中取值非整数的变量,一般选择对应系数较大的进行分枝。在【例4-1】中,x1的系数为6,大于x2的系数,且＝28/9,则分枝结果为x1≤3,x1≥4。然后将“x1≤3”和“x1≥4”作为约束条件加入松弛问题的模型(4-1)中求解,求解结果如图4-3所示,原可行域划分为两个区域,在“3＜x1＜4”区域,没有整数解,故删去。两个区域分别为LP1和LP2,最优解分别为:X(1)＝(3,20/7)T,Z(1)＝226/7;X(2)＝(4,1)T,Z(2)＝29。

第三步,第二次定界。由于Z(1)＞Z(2),因此上界为226/7(大于32)。若分枝后求出整数解,则该整数解对应的目标函数值作为下界(本题中为29)。由于29小于32,说明还没有找到最优整数解,需要进一步分枝。需要说明的是,在分枝定界的过程中,上界始终为松弛问题的最优解对应的目标函数值,且逐渐减小;下界始终为整数可行解对应的目标值,且逐渐增加,当上界和下界相等时,整数规划问题达到最优。

第四步,第二次分枝。由于LP2已经得到整数解,因此需要对LP1进行分枝。在LP1中,x1的取值已是整数(3),故只需要对x2(20/7)进行分枝,见模型(4-2)和图4-4。

图4-3

图4-4

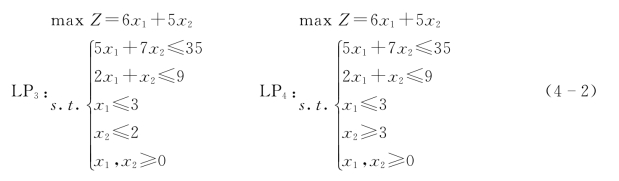
LP1分为LP3和LP4,最优解分别为:X(3)＝(3,2)T,Z(3)＝28;X(4)＝(14/5,3)T,Z(4)＝159/5。

第五步,第三次定界。由于Z(1)＞Z(4)＞Z(3),因此上界为159/5,下界不变。

第六步,第三次分枝。由于LP3已经得到整数解,只需要对LP4进行分枝。在LP4中,x2的取值已是整数(3),故只需要对x2(14/5)进行分枝,过程可见模型(4-3)和图4-5。LP4分解为两个区域LP5和LP6,LP5的最优解为:X(5)＝(2,25/7)T,Z(5)＝209/7;对于LP6,点(3,3)不在松弛问题的可行域内,因此无可行解。

第七步,第四次定界。由于Z(5)＞Z(3),因此上界为209/7。由于LP5没有得到整数解,下界仍为29。

第八步,第四次分枝。对LP5进行分枝,在LP5中,x1的取值已是整数(2),故只需要对x2(25/7)进行分枝,过程可见模型(4-4)和图4-6。LP5分解为两个区域LP7和LP8,最优解分别为:X(7)＝(2,3)T,Z(7)＝27;X(8)＝(7/5,4)T,Z(8)＝142/5。

图4-5

图4-6

第九步,第五次定界。由于Z(2)＞Z(8),因此上界为29,下界仍为29,此时该整数规划问题得到唯一最优解:X∗＝(4,1)T,Z∗＝29,分枝定界过程如图4-7所示。

图4-7(www.xing528.com)

现将分枝定界法求解步骤总结如下:

步骤1:整数规划问题为A,其松弛问题为B,设定问题A(max)的初始下界(min问题为上界)。

步骤2:求解问题B,有三种情况:

(a)B无可行解,此时问题A也无可行解,停止。

(b)B有最优解且为整数,则问题B的最优解就是问题A的最优解,停止。

(c)B有最优解但不是整数,设目标函数值为问题A的上(下)界,转入步骤3。

步骤3:分枝、定界。

步骤4:比较、剪枝。

步骤5:重复步骤3和4,直至求出最优整数解。

对于整数规划问题,经常会出现最优整数解不唯一的情况,因此分枝一定要彻底。

【例4-11】用分枝定界法求解下面整数规划问题。

解:

用图解法求解松弛问题,如图4-8所示,最优解为:X∗＝(7/2,9/5)T,Z∗＝53/10。上界为53/10,下界为0。第一次分枝,如图4-8所示,LP1最优解为:X(1)＝(3,2)T,Z(1)＝5;LP2最优解为:X(2)＝(4,6/5)T,Z(2)＝26/5。上界为26/5,下界为5。分枝定界过程可见模型(4-5)和图4-9。

图4-8

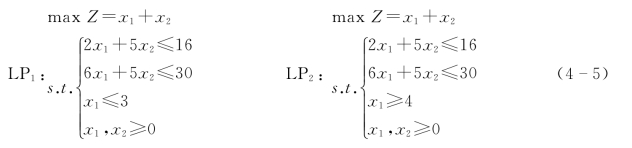
图4-9

第一次分枝得到整数解和目标函数值5,同时上界为26/5(5．2),即最优目标函数值不超过5,可以判断此时已经获得最优整数解。此时,计算尚未结束,只有当上界和下界相等并且同为整数时,计算才结束。

第二次分枝(对LP2)。如图4-10所示,LP3最优解为:X(3)＝(25/6,1)T,Z(3)＝31/6;LP4无可解。上界为31/6,下界为5。分枝定界过程可见模型(4-6)和图4-10。

第三次分枝(对LP3)。LP5最优解为:X(5)＝(4,1)T,Z(5)＝5;LP6最优解为:X(6)＝(5,0)T,Z(6)＝5。上界为5,下界为5,见模型(4-7)和图4-11,分枝定界过程如图4-12所示。因此该问题最优整数解不唯一,X(1)∗＝(3,2)T,X(2)∗＝(4,1)T,X(3)∗＝(5,0)T,Z∗＝5。

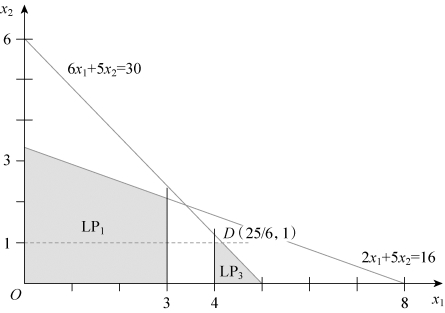
图4-10

图4-11

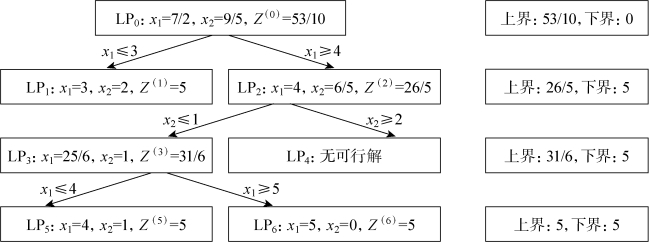
图4-12