
视频-4.1整数规划问题与数学模型-3

视频-4.1整数规划问题与数学模型-4

视频-4.1整数规划问题与数学模型-5
(1)生产基地规划问题。
【例4-4】某公司拟建设A,B两种类型的生产基地若干个,每个基地占地面积、所需经费、建成后生产能力及现有资源情况如表4-3所示,问A,B两种类型的生产基地各建设多少个,可使总生产能力最大?
表4-3

解:
设A,B两种类型的生产基地各建设x1,x2个,则其模型为:
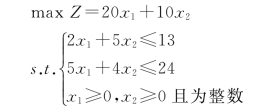
(2)人员安排问题。
【例4-5】某服务部门各时段(2小时一时段)需要服务员人数如表4-4所示,服务员连续工作8小时(4个时段)为一班。问如何安排服务员的工作时间,可使服务员总数最少?
表4-4

解:
设第j时段开始时上班的服务员人数为xj,第j时段来上班的服务员将在第j+3时段结束时下班,故决策变量只有x1,x2,x3,x4和x5,则其模型为:

(3)项目投资选择问题。
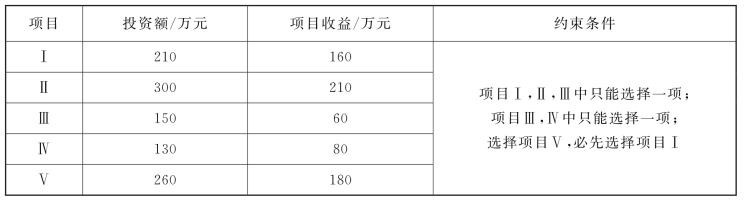
【例4-6】现有600万元,计划投资5个项目,每个项目收益如表4-5所示,求利润最大的投资方案。
表4-5
解:
设变量为xj,j=1,2,…,5。

则其模型为:
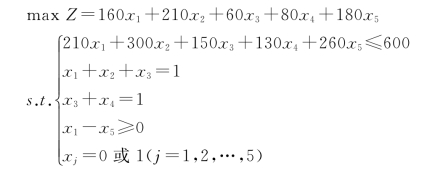
本题难点在于确定约束条件“x1≥x5”,即选择项目Ⅴ,必先选择项目Ⅰ,如表4-6所示。
表4-6
 (https://www.xing528.com)
(https://www.xing528.com)
(4)互斥约束问题。
【例4-7】某企业拟建热力车间,供热材料可以选择煤或天然气。若用煤加热,约束条件为4x1+5x2≤200;若用天然气加热,约束条件为3x1+5x2≤180。管理人员针对热力车间的建设问题建立了相关数学模型,但缺少关于供热材料的约束条件,原因是关于供热材料的选择尚未确定,且只能在两种材料中选择一种。请根据已知条件增加供热材料的约束条件。
解:
根据题意可知,只能在煤和天然气中选择一种作为供热材料,因此题中所给的两个约束条件是互相排斥的。对于此类问题,可做数学上的处理。设变量为y,即

同时引入M(M为任意大的正数),则约束条件为:
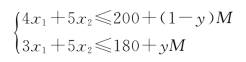
从模型中可以看出,当采用煤加热时,y=1,则约束条件“4x1+5x2≤200”起作用,约束条件“3x1+5x2≤180+y M”失效。当采用天然气加热时,y=0,则约束条件“3x1+5x2≤180”起作用,约束条件“4x1+5x2≤200+(1-y)M”失效。
(5)租赁问题。
【例4-8】某服装公司租用生产线拟生产T恤、衬衫和裤子,已知每种产品的资源消耗、售价、成本以及生产线租金等数据如表4-7所示,若每年可使用劳动力8 200 h,布料8 800 m2,问如何安排,才能使利润最大?
表4-7
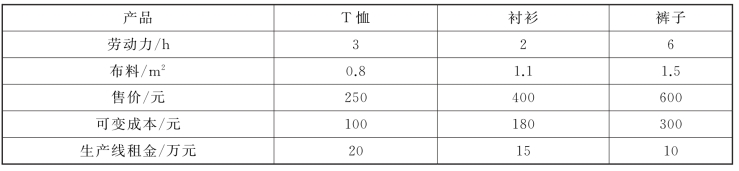
解:
设第j种服装生产量为xj,同时

则其模型为:

在建立模型时,容易出现的错误是缺少约束条件xj≤Myj(j=1,2,3),此约束条件是为了防止出现xj>0且yj=0的情况。例如,生产T恤,x1>0,此时一定租用生产线,即y1=1,如果y1=0,则不能满足约束条件x1≤My1。
(6)指派问题。
【例4-9】甲、乙、丙、丁四个人都能完成A,B,C,D四项任务,一项任务只能由一个人完成,一个人只能完成一项任务,每个人完成各项任务的时间各不相同,如表4-8所示,问如何指派,花费的总时间最短?
表4-8

解:
引入0—1变量xij,即

分析过程如下:
①完成任务所花费的总时间为:
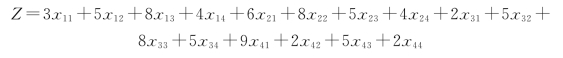
②一项任务只能由一个人完成。
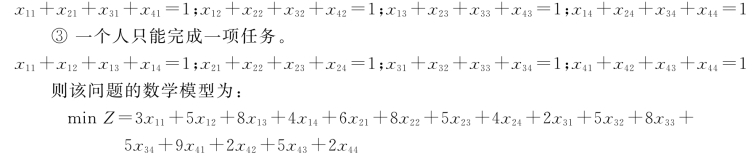
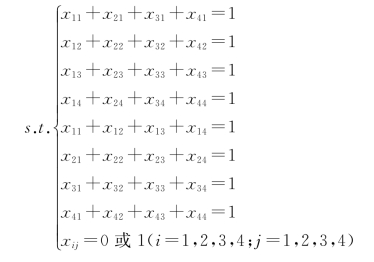
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




