运输系统中转站问题的最优方案及费用

在实际问题中,常常会遇到这种情况,需要先将物品由产地运到某个中间转运站,然后再转运到目的地。有时,经过转化的运输方案比直接运到目的地的方案更加经济。如果假定m个产地A1,A2,…,Am和n个销地B1,B2,…,Bn都可以作为中间转运站使用,那么发送物品的地点和接收物品的地点就变成了m＋n个。令ai为第i个产地的产量(净供应量),bj为第j个销地的销量(净需求量),xij为由第i个发送地运到第j个接收地的物品数量,cij为由第i个发送地到第j个接收地的单位运价,ci为第i个地点转运单位物品的费用。若将产地和销地统一编号,产地在前,销地在后,则有:

am＋1＝am＋2＝…＝am＋n＝0,b1＝b2＝…＝bm＝0

若产销平衡,即有:

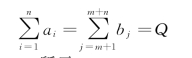
运输表和运价表如表3-28和表3-29所示。

表3-28 运输表

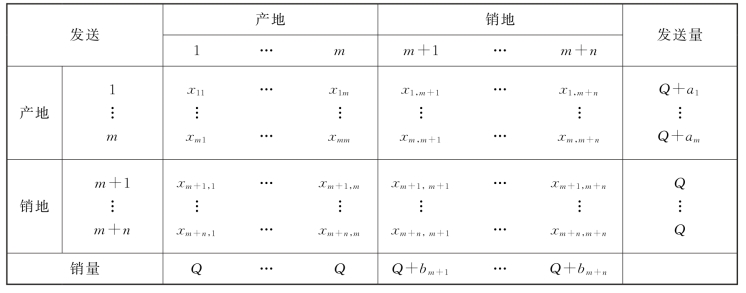
表3-29 运价表

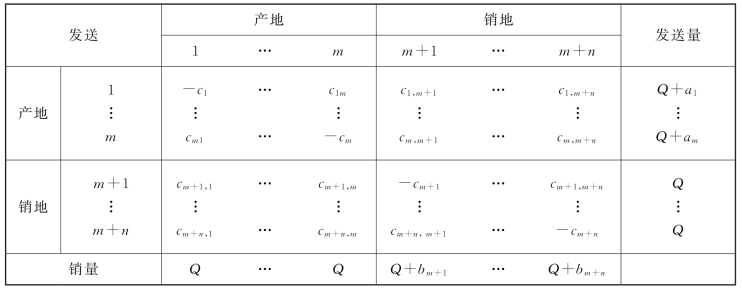
在不考虑转运费用时,可令ci＝0(i＝1,2,…,m＋n)。

【例3-11】某运输系统如图3-2所示,包括两个产地(A1与A2)、两个销地(B1与B2)和一个中间转运站(C),各产地的产量和各销地的销量用相应结点处箭线旁的数字表示,结点连线上的数字表示其间的运输单价,结点旁数字为该地的转运单价(不能直接到达,则用M表示运费),试确定最优运输方案。

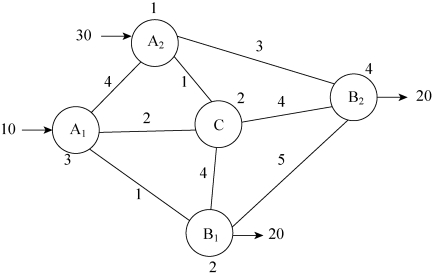
图3-2(www.xing528.com)

解:

根据题意,有aA1＝10,aA2＝30,aC＝aB1＝aB2＝0,bA1＝bA2＝bC＝0,bB1＝20,bB2＝20,Q＝10＋30＝20＋20＝40,根据表3-29计算发送量和接收量,列出运输表,如表3-30所示。

表3-30

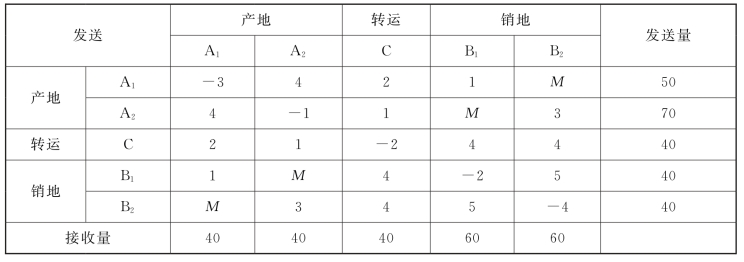
用表上作业法求解(请读者自己完成),最终结果如表3-31所示。

表3-31

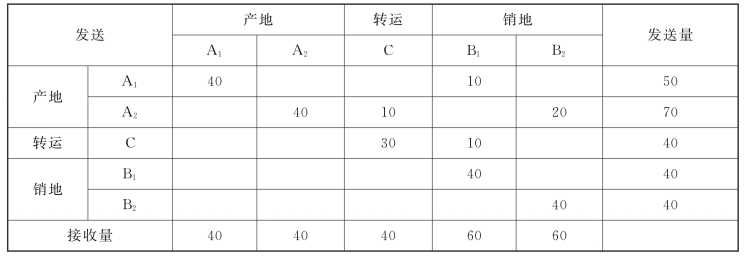
最优运输方案和费用如下:

最优运输方案A1→B1:10,费用:10×1＝10;

最优运输方案A2→B2:20,费用:20×3＝60;

最优运输方案A2→C:10,费用:10×1＝10;

最优运输方案C→B1:10,费用:10×4＝40;

以上运输费用加上转运费用(经过C的转运量为10,转运单位为2,10×2＝20),得到总费用140。