运输方案检验

视频-3．2．2表上
作业法-3-检验运输方案-闭回路法-1

视频-3．2．2表上
作业法-3-检验运输方案-闭回路法-2

确定运输方案后,可使用闭回路法和位势(对偶)变量法来进行检验,判断是否最优。

(1)闭回路法。

考察运输方案对应的运输表,从某个空格出发,沿水平或垂直方向前进,当遇到代表基变量的数字格时,顺时针或逆时针旋转90度,然后继续寻找数字格,直至回到出发点,由此形成的封闭折线叫作闭回路。例如,某一运输方案中非基变量x11所对应的闭回路如表3-19所示。

表3-19

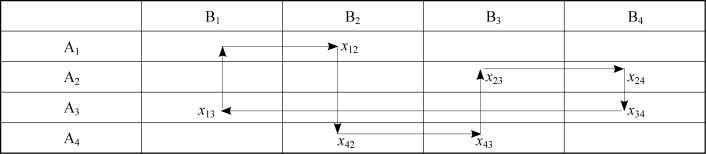
闭回路法的思路是,计算非基变量(空格)的检验数,当所有非基变量的检验数均大于等于零(非负)时,运输方案达到最优。由于任意基变量是非基变量的唯一线性组合,因此对于某一空格,有且只有唯一的闭回路。

在计算检验数时规定,起始顶点(空格)为偶数次顶点,与偶数次顶点相邻的顶点则为奇数顶点,偶数次顶点和奇数次顶点交错排列。对于闭回路来说,偶数次顶点的个数等于奇数次顶点的个数。非基变量检验数通过公式(3-5)求得。

判定定理1:当所有非基变量的检验数均大于零时,运输问题具有唯一最优方案。

判定定理2:当所有非基变量的检验数均大于等于零且有等于零的情况时,运输问题具有最优方案不唯一。

注意:对于产销平衡运输问题,其模型与线性规划标准化模型有一点区别,就是目标函数求最小值,因此判定定理也有区别,即当所有非基变量检验数大于等于零时获得最优方案。

【例3-6】用闭回路法判断【例3-3】获得的初始方案是否最优?

解:

求解过程如表3-20和表3-21所示。

表3-20

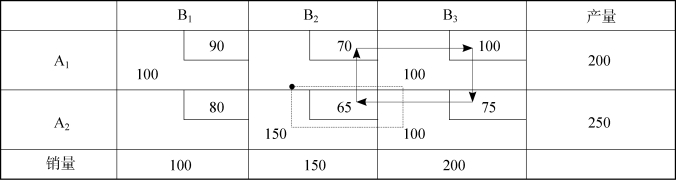
表3-21(www.xing528.com)

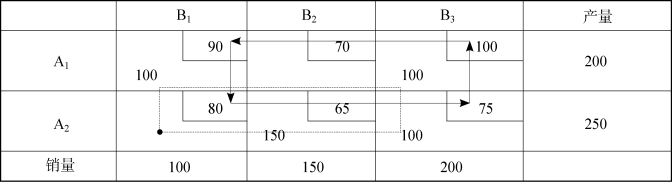
σ12＝(70＋75)－(100＋65)＝－20

σ21＝(80＋100)－(90＋75)＝15

可见,由于非基变量x12的检验数σ12小于零(－20),所以该方案不是最优。

(2)位势(对偶)变量法(以下简称位势法)。

①原理。

见式(3-4),运输问题模型的检验数σ＝C－CBB－1A,因Y＝CBB－1,σ＝C－YA,所以有σij＝cij－(ui＋vj)。

对于基变量,由于检验数为零,所以cij＝ui＋vj。

对于非基变量,σij＝cij－(ui＋vj)。

由于ui和vj取值无约束,可令u1为常数(一般令u1＝0),求得ui和vj。

②步骤。

第一步,构造位势方程组:cij＝ui＋vj,此时cij对应于基变量。

第二步,令u1为0,求得ui和vj。

第三步,求非基变量检验数σij＝cij－(ui＋vj),此时cij对应于非基变量。

【例3-7】用位势变量法判断【例3-3】获得的初始方案(见表3-7)是否最优?

解:

考察基变量x11,x13,x22,x23,构造位势方程组:cij＝ui＋vj。

令u1＝0,则u2＝－25,v1＝90,v2＝90,v3＝100。

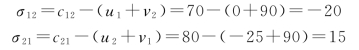
可见,用闭回路法和位势变量法求得的检验数是相同的。