产销平衡运输问题的解决方案

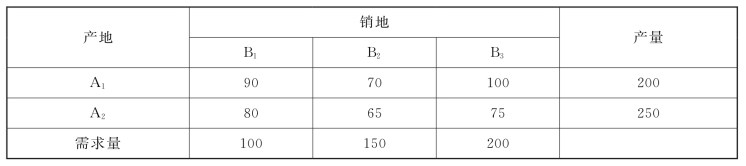
【例3-1】现有A1,A2两个产粮区,可供应粮食分别为200,250,现将粮食运往B1,B2,B3三个地区,需求量分别为100,150,200。产粮地到需求地的单位运价如表3-1所示,问如何安排运输计划,才能使总的运输费用最少?

表3-1

解:

(1)设置决策变量。

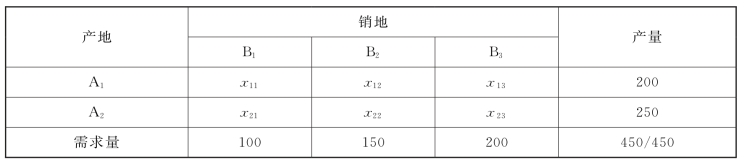
这是一个典型的产销平衡运输问题,已知每条运输路线的单位运价,为获得总的运输费用,需要确定每条运输路线的运输量,因此可设xij(i＝1,2;j＝1,2,3)为第i个产粮地运往第j个需求地的运输量,如表3-2所示。

表3-2

(2)建立目标函数。

该问题的总费用为:

S＝90x11＋70x12＋100x13＋80x21＋65x22＋75x23

总费用最小值为:

min S＝90x11＋70x12＋100x13＋80x21＋65x22＋75x23

(3)确定约束条件。

由于每个产地的产量都要运到各个需求地,因此有如下等式成立:

x11＋x12＋x13＝200(www.xing528.com)

x21＋x22＋x23＝250

同时,每个需求地的需求量均得到满足,因此有如下等式成立:

x11＋x21＝100

x12＋x22＝150

x13＋x23＝200

另外,从第i个产粮地运往第j个需求地的运输量均为非负。

综上,得到该产销平衡运输问题的数学模型:

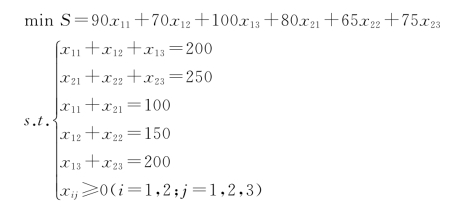
有些问题与运输问题看似没有关系,但也可以建立与运输问题形式相同的数学模型。

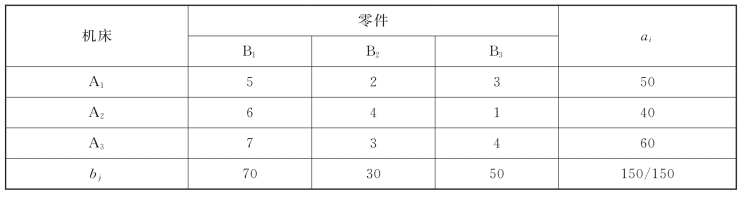
【例3-2】三台机床加工三种零件,计划第Ai台的生产任务为ai(i＝1,2,3)个零件,第j种零件的需要量为bj(j＝1,2,3),第Ai台机床加工第Bj种零件需要的时间为cij,如表3-3所示。问如何安排生产任务,才能使总的加工时间最少?

表3-3

解:

设xij(i＝1,2,3;j＝1,2,3)为第Ai台机床加工第Bj个零件的数量,则模型为:

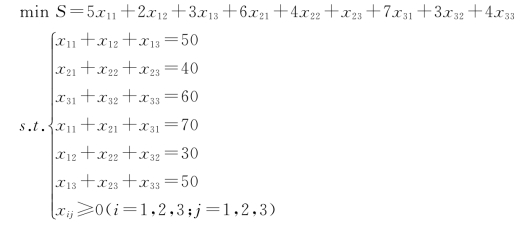
可见,遇到多方供应和多方需求的实际问题,可以考虑用产销平衡运输问题模型来进行描述。