六种食物营养成分含量和价格分析

2-1 某人根据医嘱,每天需补充A,B,C三种营养,A不少于80单位,B不少于150单位,C不少于180单位。此人准备每天从六种食物中摄取这三种营养成分。已知六种食物每百克的营养成分含量及食物价格如表2-21所示。

表2-21

(1)试建立此人在满足健康需要的基础上花费最少的数学模型。

(2)假定有一个厂商计划生产一中药丸,售给此人服用,药丸中包含A,B,C三种营养成分,试为该厂商制定一个药丸的合理价格,既使此人愿意购买,又使厂商能获得最大利益,建立数学模型。

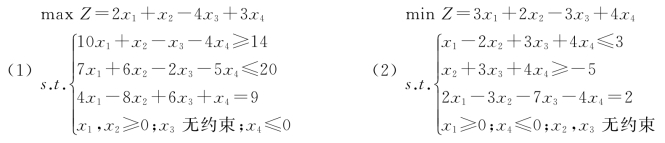
2-2 写出下面线性规划问题的对偶模型。

2-3 已知下面线性规划问题,应用对偶理论证明该问题最优解的目标函数值不大于25。

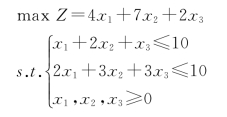
2-4 已知下面线性规划问题,已知其对偶问题的最优解为试用对偶性质求解原问题。

2-5 已知下面线性规划问题,已知原问题的最优解为X∗＝(2,2,4,0)T,试用对偶理论求出对偶问题的最优解。

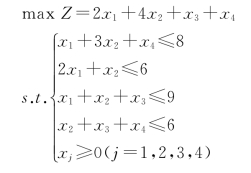
2-6 某厂拟生产甲、乙、丙三种产品,都需要在A,B两种设备上加工,有关数据如表2-22所示。

表2-22

利用对偶性质分析以下问题:

(1)如何充分发挥设备潜力,才能使产品的总产值最大?

(2)该厂如果以每台时350元的租金租外厂的A设备,是否合算?

2-7 用对偶单纯形法求解下面线性规划问题。

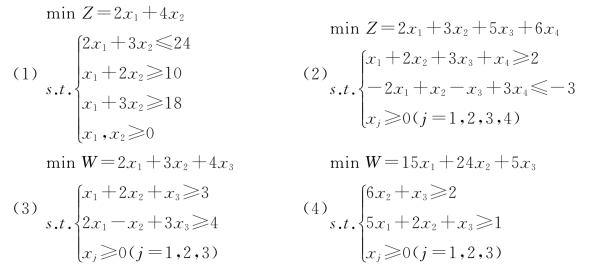
2-8 已知下面线性规划问题,要求:

(1)求最优解。(2)求c2和c3的变化范围,使得最优解不变。(www.xing528.com)

2-9 已知下面线性规划问题和最终单纯形表如表2-23所示,其中x4,x5分别为第一、第二约束方程的松弛变量,要求:

(1)对b2和c3进行灵敏度分析。

(2)增加约束条件x1＋2x2＋2x3≤12,最优解是否变化?若变化,求出最优解。

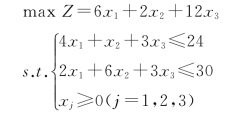
表2-23

2-10 某厂利用原料A,B生产甲、乙、丙三种产品,已知生产单位产品所需原料数、单件利润及有关数据如表2-24所示。

表2-24

要求:

(1)求使该厂获利最大的生产计划。

(2)若产品乙、丙的单件利润不变,产品甲的利润在什么范围内变化,最优解不变?

(3)若原料A市场紧缺,除拥有量外,一时无法购进,而原料B如数量不足可去市场购买,单价为0．5元,问:该厂是否应购买?以购进多少为宜?

2-11 某文教用品厂利用原材料白坯纸生产原稿纸、日记本和练习本三种产品。该厂现有工人100人,每天白坯纸的供应量为30 000千克。如果单独生产各种产品时,每个工人每天可生产原稿纸30捆或日记本30打或练习本30箱。已知原材料消耗量为:每捆原稿纸用白坯纸10/3千克,每打日记本用白坯纸40/3千克,每箱练习本用白坯纸80/3千克。已知生产各种产品的盈利为:每捆原稿纸2元,每打日记本3元,每箱练习本1元。试讨论在现有生产条件下,使该厂盈利最大的方案。如果白坯纸供应量充足,而工人数量不足,可从市场上招收临时工,临时工费用为每人每天15元,该厂应招收多少临时工为宜?

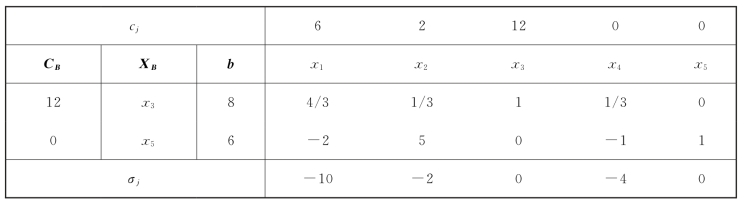
2-12 已经下面线性规划问题,要求:

(1)求参数μ＝0时的最优解。

(2)讨论μ在区间(－∞,＋∞)内解的变化。

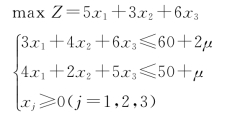
2-13 试分析当参数t≥0时,下面参数线性规划问题的最优解变化。

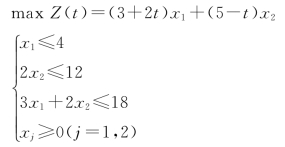
2-14 分析在t≥0时,下面线性规划问题最优解的变化。