参数线性规划优化技巧

若在线性规划问题的价值系数与资源限量中附加一个参数μ:C＝C′＋C″μ或b＝b′＋b″μ,可以分析参数在不同取值区间内最优解的变化。参数规划就是研究最优解对于参数波动的一种灵敏度分析方法。参数线性规划问题的分析步骤如下:

第一步,令λ＝0,求得最终单纯形表。

第二步,将λC∗或λb∗项反映到最终单纯形表中。

第三步,随λ值的增大或减小,观察原问题或对偶问题,一是确定单纯形表中现有解(基)允许λ值的变动范围;二是当λ值的变动超出这个范围时,用单纯形法或对偶单纯形法求得新的解。

重复第三步,一直到λ值继续增大或减小时,单纯形表中的解(基)不再出现变化时为止。

【例2-18】已知下面线性规划问题,分析λ值变化时最优解的变化。

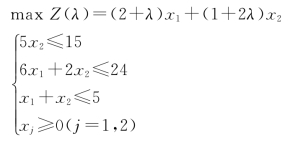
解:

第一步,先令λ＝0,求出最优解,如表2-14所示。

表2-14

第二步,将λC∗反映到最终单纯形表中,如表2-15所示。当－1/5≤λ≤1时,有最优解X∗＝(7/2,3/2,15/2,0,0)T,Z∗＝17/2＋13λ/2。

表2-15

第三步,分别计算λ＞1和λ≤－1/5时的最优解。

当λ＞1时,x4入基,x3出基,迭代过程如表2-16所示。当λ≥1时,可得最优解X∗＝(7/2,3/2,0,6,0)T,Z∗＝7＋8λ。

表2-16

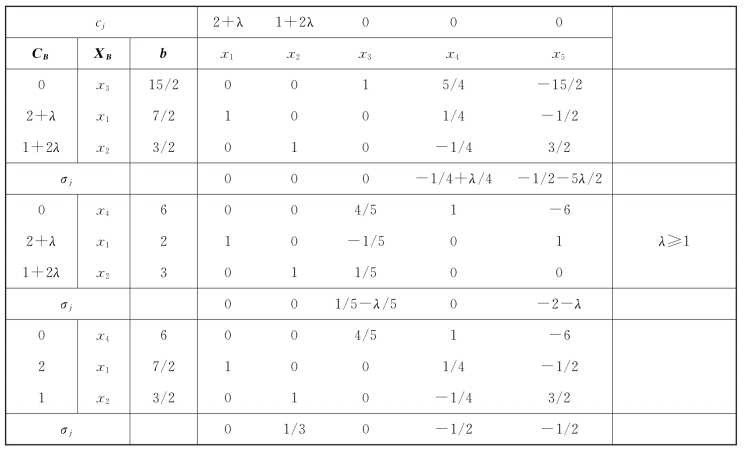
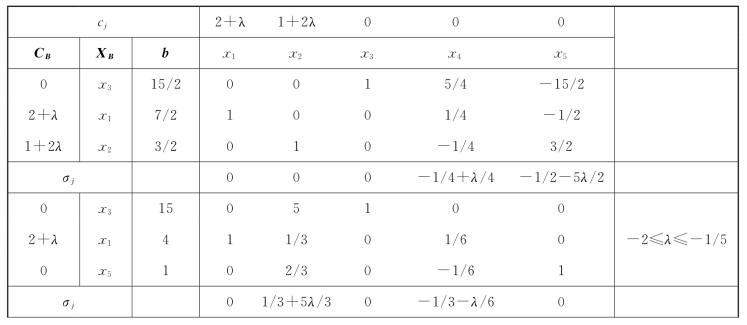
当λ≤－1/5时,x5入基,x2出基,迭代过程如表2-17所示。由于一定满足1/3＋5λ/3≤0,同时－1/3－λ/6≥0,所以x4入基,x1出基。可见,当－2≤λ≤－1/5时,Z＝8＋4λ;当λ≤－2时,Z＝0。目标函数值Z随λ变化的情况如图2-1所示。

表2-17

(www.xing528.com)

续表

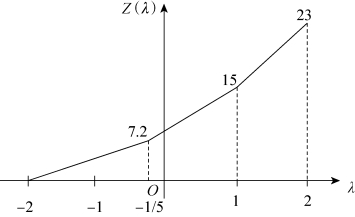
图2-1

【例2-19】已知下面线性规划问题,分析λ值变化时最优解的变化。

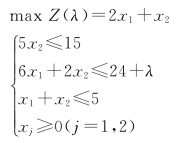
解:

第一步,先令λ＝0,求出最优解,如表2-14所示。

第二步,计算b的变化值,将λb∗项反映到最终单纯形表中。

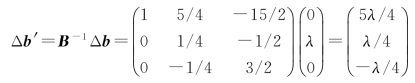
要保证最优解不变,有－6≤λ≤6(15/2＋5λ/4≥0,λ≥－6;7/2＋λ/4≥0,λ≥－7;3/2－λ/4≥0,λ≤6),此时Z∗＝17/2＋λ/4,如表2-18所示。

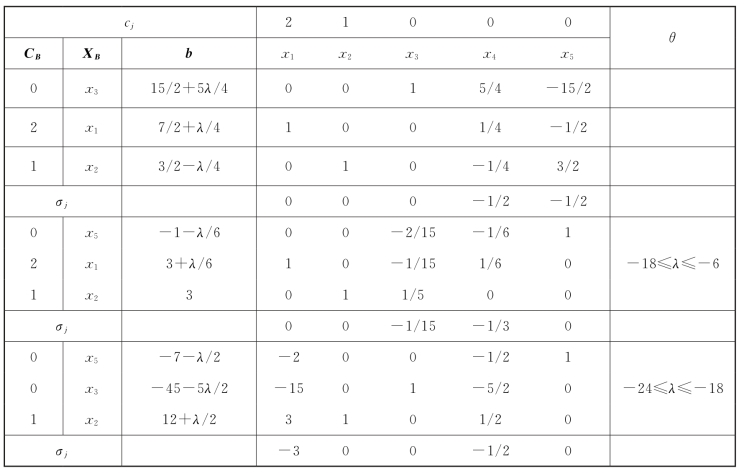
表2-18

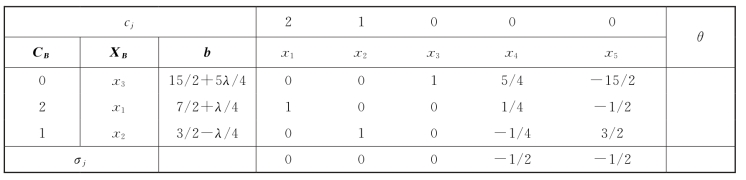
第三步,分别计算λ＞6和λ＜－6时的最优解。当λ＞6时,基变量x2＜0,用对偶单纯形法求解,x2出基,x4入基,Z∗＝10,如表2-19所示。当λ＜－6时,基变量x3＜0,用对偶单纯形法求解,x3出基,x5入基,Z∗＝9＋λ/3(－18≤λ≤－6);当λ＜－18时,基变量x1＜0,用对偶单纯形法求解,x1出基,x3入基,Z∗＝12＋λ/2(－24≤λ≤－18);当λ＜－24时,基变量x2＜0,其所在行元素均非负,不能做分母,无法选择入基变量进行迭代(不可行,因为Z不能为负值),如表2-20所示。

表2-19

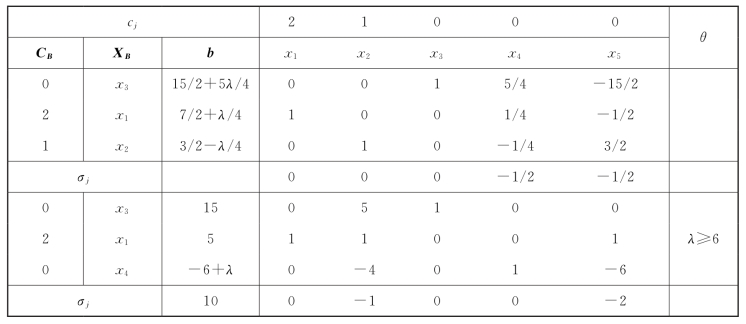
表2-20

综上,目标函数值Z随λ变化的情况如图2-2所示。

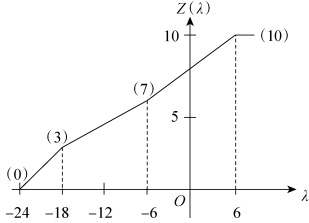
图2-2