价值系数灵敏度分析：探讨相关性

价值系数的灵敏度分析研究的内容是cj在什么范围内变化时,最优解不变。

(1)求非基变量系数CN的变化范围。

设非基变量系数的变化量为Δcj,达到最优解时,存在σ′j＝cj＋Δcj－CBB－1 Pj≤0,可得:Δcj≤CBB－1Pj－cj＝－σ∗j,即Δcj≤－σ∗j。

【例2-12】已知某线性规划问题的最终单纯形表如表2-9所示,试对非基变量x4的系数c4进行灵敏度分析。

表2-9

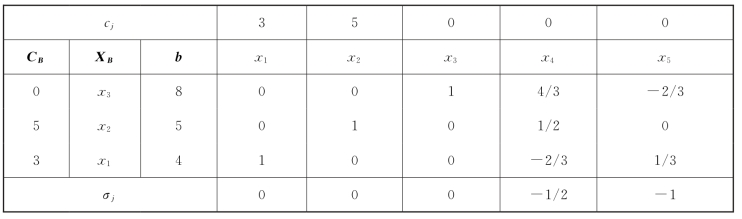
解:

由Δc4≤－σ∗4,代入数值,Δc4≤－(－1/2)＝1/2,所以,当c4≤1/2时,原问题最优解不变,仍为X∗＝(4,5,8,0,0)T,Z∗＝37。

对于价值系数的灵敏度分析,也可直接求解。令c4未知,则σ4＝c4－5×(1/2)－3×(－2/3)≤0,可得c4≤1/2。需要说明的是,若非基变量x4的系数c4变化,只影响x4的检验数。

(2)求基变量系数CB的变化范围。

【例2-13】已知某线性规划问题的最终单纯形表如表2-10所示,试对基变量x1的系数c1进行灵敏度分析。

解:

将表2-10中x1的系数改为c1,然后计算非基变量x4和x5的检验数。

表2-10

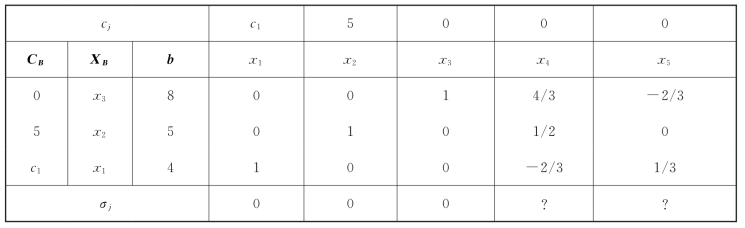
σ4＝0－5×(1/2)－c1×(－2/3)≤0,得c1≤15/4;

σ5＝0－0－c1×(1/3)≤0,得c1≥0。

综上,0≤c1≤15/4。

感兴趣的学员可自行验证,c1如果在[0,15/4]范围内变化,最优解是否发生变化?(www.xing528.com)

【例2-14】某厂生产A,B,C,D四种产品,相关数据如表2-11所示,试对价值系数c1和c3进行灵敏度分析。

表2-11

解:

设A,B,C,D四种产品的产量分别为x1,x2,x3,x4,则该问题的数学模型为:

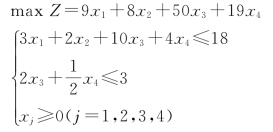
标准化:

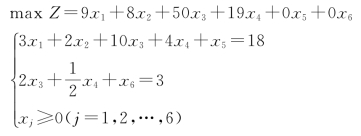
单纯形法求解过程如表2-12所示。由表2-12可知,该问题具有唯一最优解X∗＝(0,0,1,2,0,0)T,Z∗＝88。

表2-12

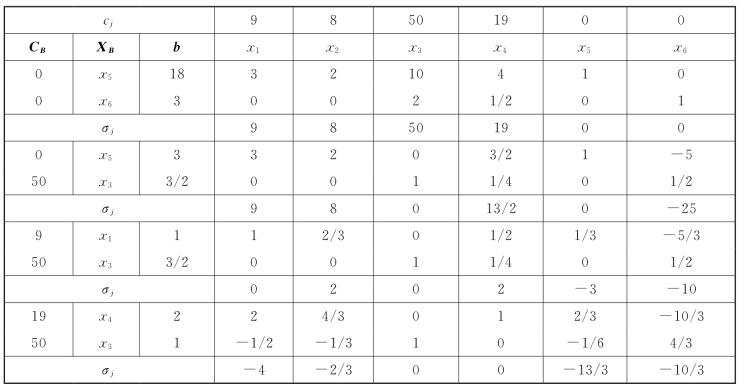
对于非基变量系数c1:

Δc1≤－σ∗1＝4,或者σ1＝c1－19×2－50×(－1/2)≤0,c1≤13,或者c1∈[－∞,13]。

对于基变量系数c3,计算非基变量x1,x2,x5,x6的检验数。

σ1＝9－19×2－(50＋Δc3)×(－1/2)≤0,Δc3≤8;

σ2＝8－19×(4/3)－(50＋Δc3)×(－1/3)≤0,Δc3≤2;

σ5＝0－19×(2/3)－(50＋Δc3)×(－1/6)≤0,Δc3≤26;

σ6＝0－19×(－10/3)－(50＋Δc3)×(4/3)≤0,Δc3≥－5/2;

综上,－5/2≤Δc3≤2,c3∈[47．5,52]。