如何使用对偶单纯形方法求解线性规划问题？

对偶单纯形法求解步骤如下:

①将原问题的数学模型标准化。

②让系统矩阵中出现单位基矩阵,基变量取值可以为负。

③列出初始单纯形表。

④判优。若所有B－1bi非负,且所有检验数非正,最优;否则,进行以下步骤。

⑤按法则B－1bl＝min{B－1bi|B－1bi＜0},确定出基变量。

⑥按法则θk＝min{σj/alj|alj＜0},确定入基变量。

⑦以alk为主元素进行迭代(方法同普通单纯形法),得到新的基可行解。

⑧重复上述④~⑦步,直至获得最优解。

【例2-11】用对偶单纯形法求解下面线性规划问题。

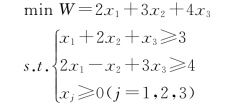
解:

①标准化:(www.xing528.com)

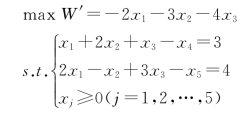
为使系数矩阵中出现单位基,将约束等式两端同乘“－1”,模型变为:

②初始单纯形表如表2-6所示。

表2-6

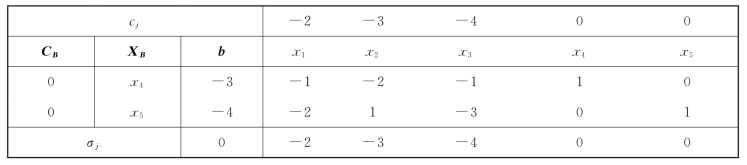
因有B－1bi小于零,该问题没有达到最优。根据出基变量确定法则(B－1b)l＝min{(B－1b)i|(B－1b)i＜0},min{－3,－4}＝(B－1b)4＝－4,因此确定x5为出基变量。根据入基变量确定法则θk＝min{σj/alj|alj＜0},min{(－2)/(－2),(－4)/(－3)}＝θ1＝1,确定x1为入基变量,由此确定主元素“－2”,迭代结果如表2-7所示。

表2-7

同理,该问题还没有达到最优。根据出基变量确定法则,min{－1}＝(B－1b)3＝－1,因此确定x4为出基变量。根据入基变量确定法则,min{(－4)/(－5/2),(－1)/(－1/2)}＝θ2＝8/5,确定x2为入基变量,由此确定主元素“－5/2”,迭代结果如表2-8所示。

表2-8

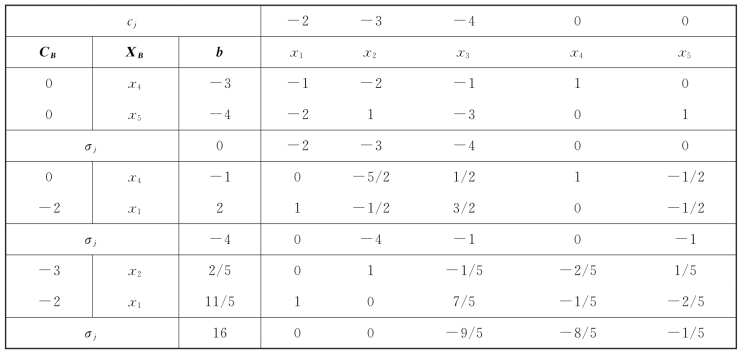
由于所有的B－1bi≥0,且σj≤0,该问题有最优解:X∗＝(11/5,2/5,0,0,0)T,Y∗＝(8/5,1/5,0,0,9/5),W∗＝－(－28/5)＝28/5。