非常规线性规划模型的对偶形式优化

非常规线性规划模型包括约束条件为等式和决策变量取值无约束的模型。

(1)约束条件为等式。

若原问题模型为:

因AX＝b⇔b≤AX≤b,原模型可转化为:

根据模型(1-11)和(2-2)可转化为对偶形式,化简过程如下:

最终得到非常规线性规划问题的对偶模型:

【例2-2】已知下列线性规划问题的数学模型,请写出对偶问题的数学模型。

解:

已知C＝(6,4),b＝(10,8)T,A＝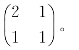

因原问题模型中约束条件个数为2,可设对偶问题变量分别为y1和y2,则有Y＝(y1,y2),Yb＝(y1,y2)×(10,8)T＝10y1＋8y2,YA＝(2y1＋y2,y1＋y2),同时YA≥C,因此,对偶问题的数学模型为:

根据模型(1-11)和(2-2)的对偶关系,原问题第一个约束条件对应于对偶问题第一个变量y1,约束条件不等式符号是“≤”,因此y1的取值范围是“≥0”。由模型(2-3)和(2-4)的对偶关系可知,原问题第二个约束条件是等式,则对偶问题第二个变量y2取值无约束。因此,若原问题模型为:

则对偶问题的数学模型为:

【例2-3】写出下面线性规划问题的对偶模型。

解法一:先将其化成常规形式,令Z＝Z′,同时将x1＋2x2＝5写成x1＋2x2≤5和x1＋2x2≥5,则模型转化为:

已知C＝(－4,－5),b＝(－3,5,－5)T,A＝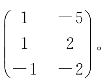

因原问题中约束条件个数为3,可设对偶问题变量分别为y1,y2,y3,则有Y＝(y1,y2,y3),Yb＝(y1,y2,y3)×(－3,5,－5)T＝－3y1＋5y2－5y3,YA＝(y1＋y2－y3,－5y1＋2y2－2y3),同时YA≥C,因此,对偶问题的数学模型为:(www.xing528.com)

令W＝－W′,y′2＝y3－y2,则对偶问题的数学模型为:

需要说明的是,若令y′2＝y2－y3,则模型将变为:

由于决策变量y′2取值无约束,因此两种结果相同。

解法二:令Z＝－Z′,将原问题模型转化为:

直接使用模型(2-3)和(2-4)以及(1-11)和(2-1)的对偶关系,得到对偶模型:

再令W＝－W′,整理后模型变为:

由此可见,两种解法得到的结果相同,但是转化过程存在较大差异。对于第一种方法来说,模型转化过程较复杂,计算量大,但是有利于理解相关知识,如线性规划模型矩阵表达式中的参数及相互关系;对于第二种方法,由于直接使用推导结果,使模型转化过程更加简单。

(2)决策变量取值无约束。

已知线性规划模型:

令X＝X′－X″,模型转化过程如下:

即

【例2-4】请写出下面线性规划问题的对偶模型。

解:

由于x1和x2对应的取值均为“≥0”,因此对偶问题的前两个约束条件不等式符号是“≥”。x3对应于对偶问题的第三个约束条件,因此对偶问题中第三个约束条件不等式符号是“＝”。综上,对偶问题的数学模型为: