无添人工变量的大M法求解线性规划问题

大M单纯形法,简称大M法,是指通过添加人工变量构成单位基,进而求解线性规划问题的方法。

【例1-18】求解下面线性规划问题:

视频-1．4大M单纯形法

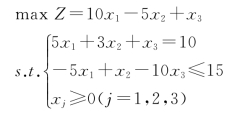
解:

①标准化:

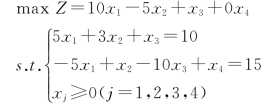
系数矩阵为:

该系数矩阵中不存在单位基,因此需要一个列向量构成单位基,加入列向量后的系数矩阵为

这时可以在模型中加入人工变量x5,x5如果等于零,则与原模型相同,若不等于零,则原线性规划问题不可行。因此在添加人工变量的同时,目标函数中的人工变量前面需要加入系数－M(M为任意大的正数),原模型变为:

该模型求解后,若人工变量等于零,则与原问题相同;若人工变量不为零,则目标函数值为“－∞”,那么原问题的最大化目标不能实现,因此称－M为惩罚系数。

②换基迭代,过程如表1-25所示。

表1-25

所有非基变量检验数均小于零,所以此题具有唯一最优解:X∗＝(2,0,0,25,0)T,Z∗＝20。

【例1-19】求解下面线性规划问题:(www.xing528.com)

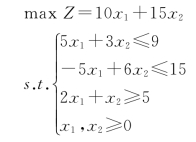
解:

①标准化:

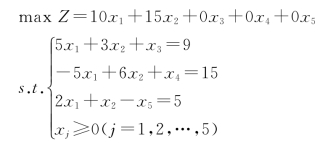
系数矩阵为:

添加人工变量后系数矩阵为:

模型变为:

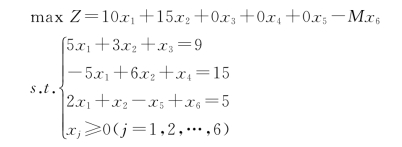
②换基迭代,过程如表1-26所示。若按判定定理1,该问题存在唯一最优解。但是,在单纯形表中,人工变量x6的取值不为零(7/5),因此该问题不可行。

表1-26

在使用大M法求解线性规划问题时,可能有以下结果:

①基变量中不含人工变量;

②基变量中含人工变量,但人工变量取值为零;

③基变量中含人工变量,但人工变量取值不为零。

只在前两种情况下,线性规划问题有最优解,对于第③种情况,线性规划问题无可行解。

判定定理4:在添加人工变量的单纯形表中,若B－1b非负,且所有检验数均小于等于零,如果基变量中含有人工变量且取值不为零,则该线性规划问题不可行或无可行解。