最优解判定定理

判定定理1:在单纯形表中,若所有非基变量的检验数都小于零,且B－1b均为非负,则线性规划问题具有唯一最优解。

在【例1-14】中,在最终单纯形表1-21中,非基变量x3和x4的检验数均小于零,则线性规划问题只有一个最优解,这种情况称作唯一最优解。

【例1-15】用单纯形法求解下面线性规划问题:

视频-1．3普通单纯形法-6迭代过程2

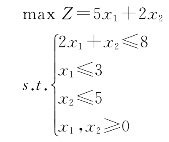
解:将模型标准化,迭代过程如表1-21所示。

视频-1．3普通单纯形法-7迭代过程3

表1-21

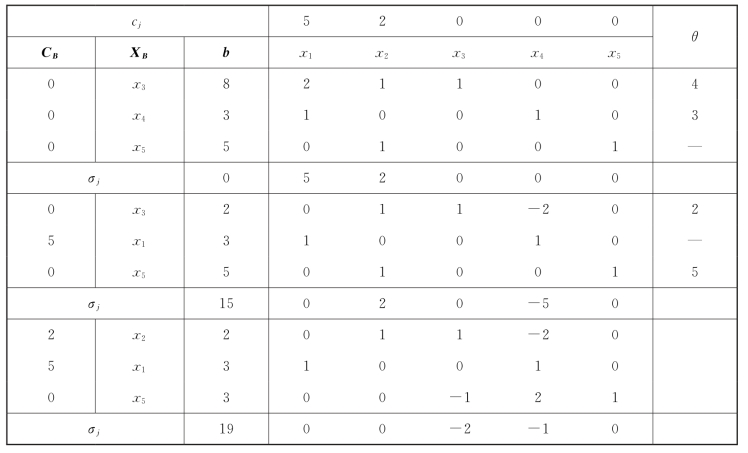
唯一最优解为X∗＝(3,2,0,0,3)T,Z∗＝19。

判定定理2:在单纯形表中,若所有非基变量的检验数都小于等于零,且B－1b均为非负,同时存在非基变量的检验数等于零的情况,则线性规划问题具有无穷多最优解(多重最优解)。

【例1-16】用单纯形法求解下面线性规划问题:

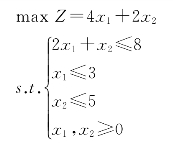
解:

①标准化:

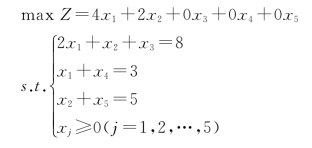(www.xing528.com)

②迭代过程如表1-22所示。

表1-22

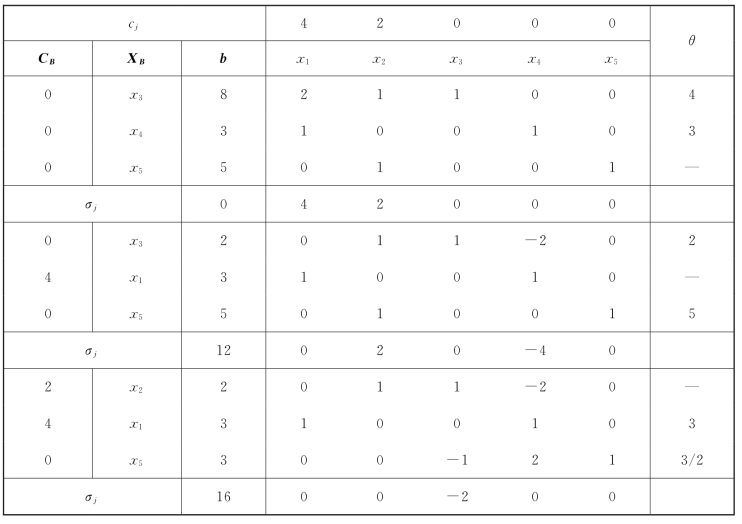
根据判定定理2,【例1-16】具有无穷多最优解,或称多重最优解。在表1-22中,若选择x4入基,x5出基,迭代过程如表1-23所示,在此基础上每迭代一次,都会获得一个最优解,目标函数值均为16。所以,求解结果为无穷多最优解,其中两个解为(3/2,5,0,0,3/2)T,Z∗＝16。

表1-23

判定定理3:在单纯形表中,若某个非基变量的检验数σk大于零且为最大,可确定变量xk入基,但xk对应列向量的元素均为非正,因而无法确定出基变量,则线性规划问题具有无界解。

【例1-17】用单纯形法求解下面线性规划问题:

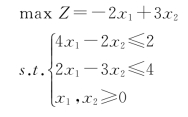
解:

①标准化:

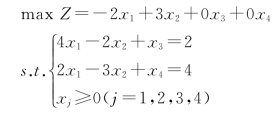
②迭代过程如表1-24所示。

表1-24

由初始单纯形表可知,非基变量x2的检验数(3)大于零,该线性规划问题没有达到最优。可选择x2作为入基变量,但由于不满足出基变量确定法则(aij＜0),所以出基变量无法确定。虽然不能确定x3和x4中哪个变量出基,但无论哪个变量出基,都必须满足:

由于x2入基(x2≥0),变量x3和x4的取值都大于等于零,若x2无限增大,目标函数值就可以无限增大,因此该问题具有无界解。

判定定理4(无可行解判定定理)与大M单纯形法有关,因此在1．4节中介绍。