普通单纯形法求解步骤及案例分析

(1)普通单纯形法求解思路。

掌握了上述概念以后,根据图解法的启示,可以确定线性规划问题的解题思路,如图1-8所示。首先,确定一个初始基可行解。然后,判断这个基可行解是不是最优解,如果是最优解,求解结束;如果不是最优解,寻找另一个基可行解,再重复上述步骤,直至找到最优解。

(2)普通单纯形法原理。

对于公式(1-11),可令A＝(P1,P2,…,Pm,Pm＋1,…,Pn),其中P1,P2,…,Pm为基变量对应的列向量;Pm＋1,Pm＋2,…,Pn为非基变量对应的列向量,因此,A可写成A＝(B,N),相应地,X＝(XB,XN)T,C＝(CB,CN)。

视频-1．3普通单纯形法-5迭代过程1

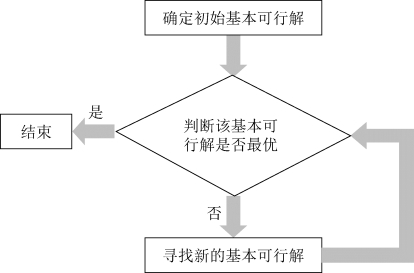
图1-8

对于约束条件AX＝(B,N)(XB,XN)T＝BXB＋NXN＝b,在等式两端左乘B－1,有XB＋B－1 NXN＝B－1b,即XB＝B－1b－B－1 NXN。若令XN＝0,则X＝(B－1b,0)T。

对于目标函数Z＝CX＝(CB,CN)(XB,XN)T＝CB XB＋CN XN,将XB＝B－1b－B－1 NXN代入后,有Z＝CB(B－1b－B－1 NXN)＋CN XN＝CBB－1b＋(CN－CBB－1 N)XN,令XN＝0,则Z＝CBB－1b。对于非基变量,检验数用σN＝CN－CBB－1N来表示;对于某一非基变量的检验数,也可表示为σj＝cj－Zj。对于基变量,检验数为σB＝CB－CBB－1B＝0。因此,所有检验数可表示为σ＝C－CBB－1A。上述推导过程可用表1-14和表1-15表示(其中,E为单位矩阵,即B－1B＝E),称为单纯形表。

表1-14

表1-15

(3)普通单纯形法求解步骤。

①求出初始基本可行解。

先将模型标准化,找到单位基,令非基变量为零,确定初始基本可行解。

②最优性检验。

利用公式σN＝CN－CBB－1 N求出非基变量检验数,若所有非基变量检验数小于或等于零,说明已得到最优解,否则进入步骤③。

③换基和迭代。

(a)确定入基变量σk＝max{σj|σj＞0}(入基变量确定法则);

(b)确定出基变量θl＝min{bi/aik|aik＞0}(出基变量确定法则或最小比值法则);

(c)确定主元素,考察入基变量对应的列向量和出基变量对应的行向量,交叉元素即为主元素;

(d)先将主元素变为“1”,再利用初等变换方法求出新的基本可行解。

④重复步骤②和③,直到求出最优解。

举例之前,可以熟悉用消元法求解线性规划问题。

【例1-14】用单纯形法求解【例1-1】的线性规划问题。

解:

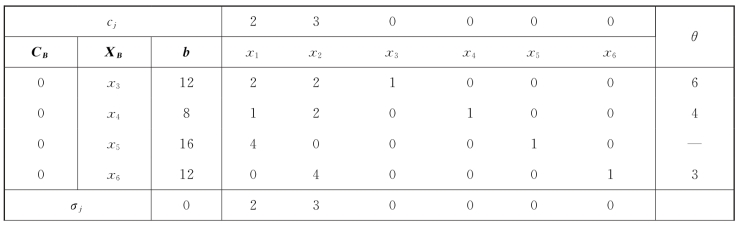
①确定初始基本可行解模型。先将模型标准化,并将数据填入初始单纯形表1-16中,可知初始基可行解为X(0)＝(0,0,12,8,16,12)T,Z(0)＝0。

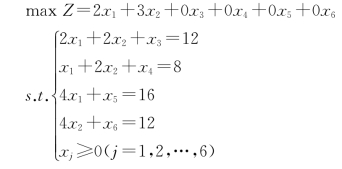
用消元法求解线性规划问题

表1-16

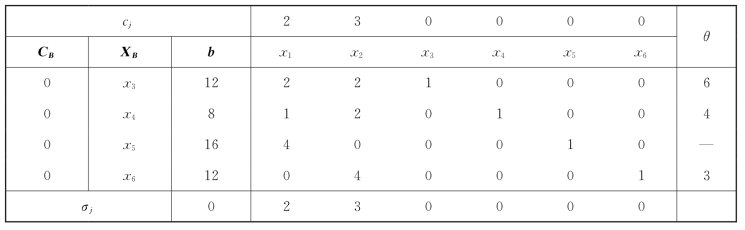
②检验(第1次)。由于单纯形表中x1和x2的检验数2和3均大于零,说明X(0)不是最优解。

③换基(第1次)。根据入基变量确定法则,非基变量x2的检验数(3)最大,因此选x2为入基变量。按最小比值法则,θ4＝min(12/2,8/2,－,12/4)＝3,选x6为出基变量。

④迭代(第1次)。首先,确定主元素,入基变量x2对应的列向量(2,2,0,4)T和出基变量x6对应的行向量(12,0,4,0,0,0,1),交叉元素“4”为主元素;将主元素“4”变为“1”,即对应行向量的每一个元素都除以4,同时将原基变量x6及系数c6(0)替换成x2和c2(3)。然后,使用初等行变换方法,将入基变量x2对应的列向量(2,2,0,1)T中除主元素“1”以外的元素均变为“0”,与原基变量x6对应的列向量(0,0,0,1)T相同,即让原基变量x3,x4,x5和新入基的变量x2对应的列向量构成新的单位基,求出新的基可行解,这就是换基的目的。最后,根据公式σN＝CN－CBB－1N,计算非基变量(x1和x6)的检验数:

σ1＝c1－CBB－1P1＝2－(0,0,0,3)(2,1,4,0)T＝2

σ6＝c6－CBB－1P6＝0－(0,0,0,3)(－1/2,－1/2,0,1/4)T＝－3/4(www.xing528.com)

如表1-17所示,得到一个新的基可行解:X(1)＝(0,3,6,2,16,0)T,Z(1)＝9。

表1-17

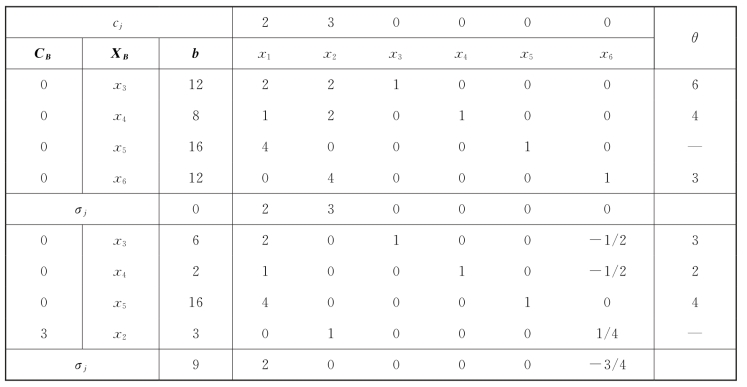
⑤检验(第2次)。由于单纯形表中x1的检验数2大于零,说明X(1)不是最优解。

⑥换基(第2次)。根据入基变量确定法则,非基变量x1的检验数(2)最大,因此选x1为入基变量。按最小比值法则,θ2＝min(6/2,2/1,16/4,－)＝2,选x4为出基变量。

⑦迭代(第2次)。首先确定主元素,入基变量x1对应的列向量(2,1,4,0)T和出基变量x4对应的行向量(2,1,0,0,1,0,－1/2),交叉元素“1”为主元素。然后,使用初等行变换方法,将入基变量x1对应的列向量(2,1,4,0)T中除主元素“1”以外的元素均变为“0”,与原基变量x4对应的列向量(0,1,0,0)T相同,即让原基变量x3,x5,x2和新入基的变量x4对应的列向量构成新的单位基,求出新的基可行解。最后,计算非基变量(x4和x6)的检验数:

σ4＝c4－CBB－1P4＝0－(0,2,0,3)(－2,1,－4,0)T＝－2 σ6＝c6－CBB－1P6＝0－(0,2,0,3)(1/2,－1/2,2,1/4)T＝1/4

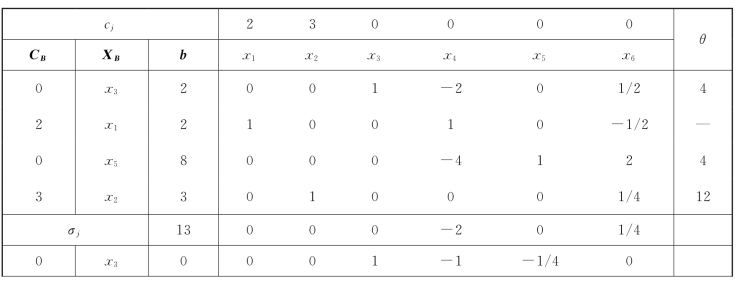
如表1-18所示,得到一个新的基可行解:X(2)＝(2,3,2,0,8,0)T,Z(2)＝13。

表1-18

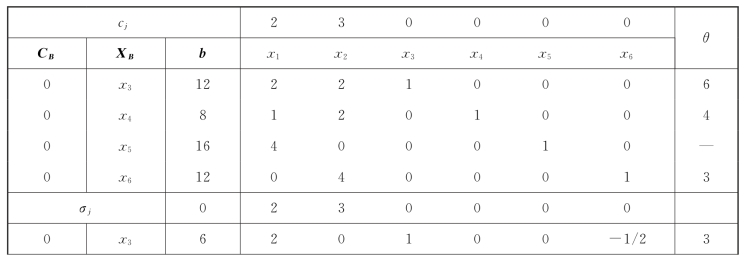
续表

⑧检验(第3次)。由于单纯形表中x6的检验数1/4大于零,说明X(2)不是最优解。

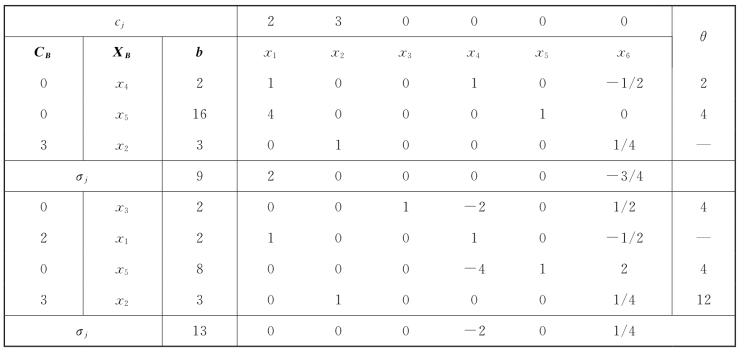
⑨换基(第2次)。根据入基变量确定法则,非基变量x6的检验数(1/4)最大,因此选x6为入基变量。按最小比值法则,θ2＝min[2/(1/2),－,8/2,3/(1/4)]＝4,选x3为出基变量(Bland法则)。

⑩迭代(第3次)。首先确定主元素,入基变量x6对应的列向量(1/2,－1/2,2,1/4)T和出基变量x3对应的行向量(2,0,0,1,－2,0,1/2),交叉元素“1/2”为主元素,先将主元素变为“1”。然后,使用初等行变换方法,将入基变量x6对应的列向量(1,－1/2,2,1/4)T中除主元素“1”以外的元素均变为“0”,与原基变量x3对应的列向量(1,0,0,0)T相同,即让原基变量x1,x5,x2和新入基的变量x6对应的列向量构成新的单位基,求出新的基可行解。最后,计算非基变量(x3和x4)的检验数:

σ3＝c3－CBB－1P3＝0－(0,2,0,3)(2,1,－4,－1/2)T＝－1/2

σ4＝c4－CBB－1P4＝0－(0,2,0,3)(－4,－1,4,1)T＝－1

如表1-19所示,得到一个新的基可行解:X(3)＝(4,2,0,0,0,4)T,Z(3)＝14。由于检验数均小于等于零,所以此基可行解是最优解,即X∗＝(4,2,0,0,0,4)T,Z∗＝14。需要指出的是,该解为退化解(解中的某个基变量等于零),基变量x5等于零。

表1-19

续表

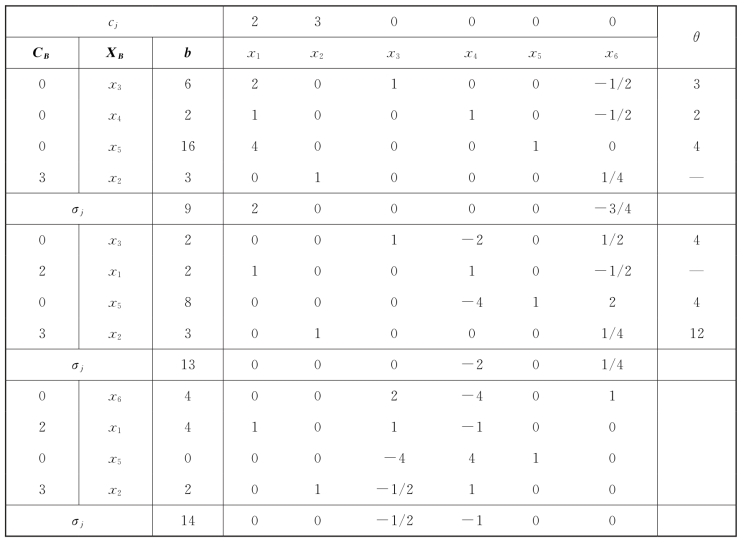
在前面用最小比值法确定出基变量时,有两个最小比值“4”,如果不按照Bland(布兰德)法则,可以选择x6入基,x5出基,计算结果如表1-20所示,此时最优解为X∗＝(4,2,0,0,0,4)T,Z∗＝14。该最优解也是退化解,基变量x3等于零。

表1-20

由此可见,单纯形法的求解过程就是不断寻找更优的基可行解(对应凸多边形的顶点)的过程,最终在凸多边形(可行域)的顶点找到唯一最优解,对于上例,可将单纯形法和图解法的求解结果进行比较,如图1-9所示。

续表

O点(0,0):X(0)＝(0,0,12,8,16,12)T,Z(0)＝0。

A点(0,3):X(1)＝(0,3,6,2,16,0)T,Z(1)＝9。

B点(2,3):X(2)＝(2,3,2,0,8,0)T,Z(2)＝13。

C点(4,2):X∗＝(4,2,0,0,0,4)T,Z∗＝14。

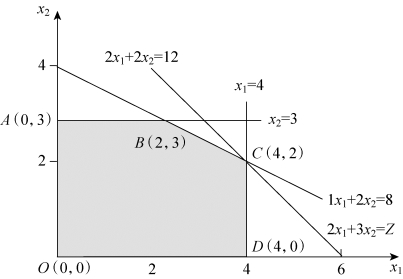
图1-9

(4)退化解与Bland法则。

一般称基变量取值为零的解为退化解。在确定出基变量时,有时存在两个以上相同的最小比值,这样在下一次迭代中就有一个或几个基变量等于零,这就出现了退化解。当出现退化时,进行多次迭代,而基从B1,B2,…又返回到B1,计算过程陷入循环,在理论上无法得到最优解。Bland法则就是针对这种现象提出的:

①在确定入基变量时,若存在两个或两个以上的最大检验数(大于零),选择下标号最小的变量入基。例如,非基变量x2和x4的检验数均为3,按照Bland法则,应选择x2入基。

②在确定出基变量时,若存在两个或两个以上的最小比值,同样选择比值对应下标号小的变量出基。

思考:对于【例1-12】,若不使用Bland法则,会得到什么样的结果?