线性规划标准化模型中的重要概念

(1)基。

假设线性规划问题模型的系数矩阵为m行n列,则系数矩阵中秩为m的m行和m列子矩阵称为基矩阵,简称为基,一般用B来表示。

视频-1．3普通单纯形法-3重要概念1

已知线性规划标准化模型(1-12)的系数矩阵A为2行4列,见矩阵(1-13),其中2行2列的子矩阵有个,如表1-12所示。

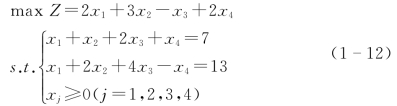
视频-1．3普通单纯形法-4重要概念2

表1-12

容易判断,B4中两个行(或列)向量线性相关,即对应元素成比例,其余子矩阵均为满秩矩阵,因此该线性规划模型存在5个基:B1,B2,B3,B5和B6。(www.xing528.com)

(2)基变量和非基变量。

基中的列向量对应的变量称为基变量,决策变量中除基变量以外的变量称为非基变量。如B1中的两个列向量分别对应于决策变量x1和x2,则x1和x2为基变量,x3和x4为非基变量。

(3)基本解。

对于某一确定的基,令所有非基变量为0,通过约束方程组AX＝b可解出m个基变量的唯一解,称之为基本解。基矩阵B1,B2,B3,B5和B6对应的基本解如表1-13所示。

(4)基本可行解。

变量取值满足非负条件的基本解称为基本可行解,基本可行解对应于凸多边形(凸集)的顶点。如表1-13所示,X1,X2,X5和X6为基本可行解,分别对应于该问题可行域(凸多边形)的四个顶点。

表1-13

思考:已知线性规划模型为:

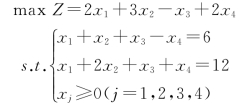
问:在A＝(2,0,4,0)T,B＝(6,0,3,3)T,C＝(3,2,3,2)T和D＝(0,6,0,0)T中,哪一个是基本可行解?