解可能性：1、2、3线性规划问题的优化方法

线性规划问题的解有多种可能,具体见【例1-9】、【例1-10】、【例1-11】和【例1-12】,求解过程和结果如图1-4、图1-5、图1-6和图1-7所示。

(1)唯一最优解。

【例1-9】用图解法求解下面线性规划问题:

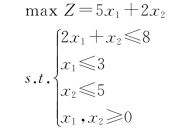
解:

按照图解法求解步骤求解,结果如图1-4所示。

唯一最优解:X∗＝(3,2)T,Z∗＝19。

思考:如果目标函数变为max Z＝3x1＋2x2,求解结果会发生什么变化?

(2)无穷多最优解。

【例1-10】用图解法求解下面线性规划问题:

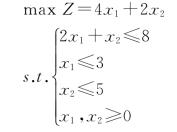
解:

按照图解法求解步骤求解,结果如下:

对于两个变量的线性规划问题,若目标函数等值线的斜率与某一约束条件对应的直线相同,则该问题具有无穷多最优解,如图1-5所示,说明在AB线段上所有x1和x2的组合都是最优解。求解结果为X1＝(3/2,5)T,X2＝(3,2)T,X＝αX1＋(1－α)X2(0≤α≤1),Z∗＝16。

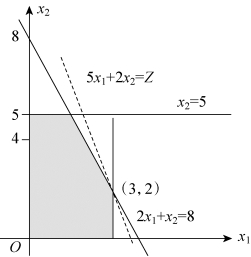
图1-4

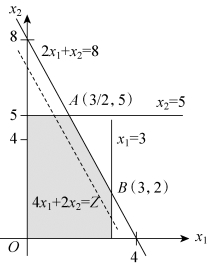
图1-5

思考:对于【例1-10】,是否可以从模型中直接得到max Z?

(3)无界解。(www.xing528.com)

【例1-11】用图解法求解下面线性规划问题:

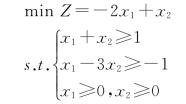
解:

求解过程和结果如图1-6所示,由于可行域无界,目标值可以无限增大,所有本题为无界解,出现这种情况的原因是,建模时忽略了必要的限制约束,使得决策变量的取值无限制,导致目标函数值无下界。

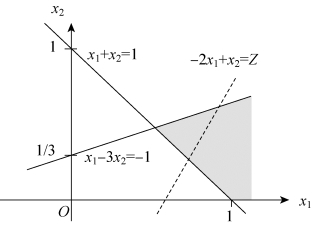
图1-6

思考:如果【例1-11】求目标最大值,结果如何?

(4)无可行解。

【例1-12】用图解法求解下面线性规划问题:

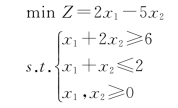
解:

求解过程和结果如图1-7所示,该线性规划问题的可行域是空集,所以本题为无可行解,出现这种情况的原因是,模型中的约束条件相互矛盾。

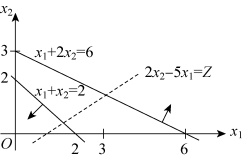
图1-7

图解法的解题思路和几何上的直观表示,对求解线性规划问题有以下重要启示:

①线性规划问题的解有唯一最优解、无穷多最优解、无界解和无可行解四种情况。

②线性规划问题的可行域一般为无界或有界凸多边形(无可行解除外)。

③若线性规划问题的最优解存在,即有唯一最优解或无穷多最优解,则必然在可行域的某个顶点上获得。

④若可行域中有两个顶点均对应于最优解,则该两点连线上的任意一点都对应于最优解。