【摘要】:关于线性规划问题解的特性,可归纳为以下三点:①线性规划问题若有可行域,则可行域必是一个凸多边形,对应于凸集。图1-2凸集的数学定义:如图1-3所示,设K为n维欧氏空间的一个点集,若K中任意两个点X1和X2连线上的所有点都属于K,即X=αX1+(1-α)X2∈K,则称K为凸集。为此,可以得到线性规划问题的求解思路,找出并比较凸多边形(可行域)的顶点,目标函数值最大(或最小)的顶点对应于最优解。
关于线性规划问题解的特性,可归纳为以下三点:
①线性规划问题若有可行域,则可行域必是一个凸多边形,对应于凸集(集合内部任意两点连线上的点都属于这个集合)。在图1-2中,只有图1-2(a)可以用来表示凸集。

图1-2
凸集的数学定义:如图1-3所示,设K为n维欧氏空间的一个点集,若K中任意两个点X1和X2连线上的所有点都属于K,即X=αX1+(1-α)X2∈K(0≤α≤1),则称K为凸集。设X(x1,x2,…,xn),X1(u1,u2,…,un),X2(v1,v2,…,vn)。
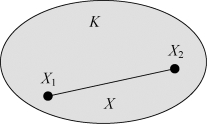
图1-3(https://www.xing528.com)
X=αX1+(1-α)X2∈K(0≤α≤1)的证明思路如下:

(vi-xi)=α(vi-ui)⇒xi=αui+(1-α)vi⇒X=αX1+(1-α)X2(i=1,2,…,n)
②凸多边形(可行域)的顶点是有限的,每个顶点对应基本可行解。关于基本可行解的概念,将在1.3节中学习。
③对于某一线性规划问题,如果有最优解,则最优解一定在可行域的某个顶点获得。
为此,可以得到线性规划问题的求解思路,找出并比较凸多边形(可行域)的顶点,目标函数值最大(或最小)的顶点对应于最优解。可见,在求解线性规划问题的时候,只需要考虑凸多边形的顶点,并比较这些顶点对应的目标函数值,就能获得最优解。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




