典型问题：成本最小化优化

(1)设备租赁问题。

设备租赁问题是在既定任务下求费用最小化的典型问题。

【例1-5】某建筑工地负责人打算租赁甲、乙两种机械安装A,B,C三种构件,这两种机械每天的安装能力、租赁费用以及工程任务如表1-7所示,问:如何租赁甲、乙两机械才能使总的租赁费用最低?

表1-7

解:

①分析问题,明确目标。设备租赁问题是已知任务,求成本最小的典型问题,即租赁多少天才能完成任务,还可以使成本最低。

②变量设置。由题意可知,总的租赁费用与两种设备的租赁天数有关,现已知租赁两种机械一天的费用,故只要确定租赁天数,就可以确定总的租赁费用,所以不妨设甲、乙设备的租赁天数分别为x1和x2,且取值非负,即若租赁,则变量大于零,若不租赁,则变量等于零。

③目标函数。总的租赁费用最小值为min Z＝250x1＋350x2。

④约束条件。两种设备每天安装构件的数量如表1-8所示,构件A,B,C的安装数量分别为5x1＋6x2,8x1＋6x2和10x1＋20x2。由题意可知,三种构件的安装任务不少于250,300和700根,因此有:5x1＋6x2≥250,8x1＋6x2≥300,10x1＋20x2≥700。

表1-8

综上,该问题的数学模型为:

(2)下料问题。

【例1-6】装修公司需要用5 m长的塑钢材料制作A,B两种型号的窗架,两种窗架所需材料规格及数量如表1-9所示,问:怎样下料才能使用料最少?(切割损失不计)

视频-1．1线性规划问题与模型-5下料问题

表1-9

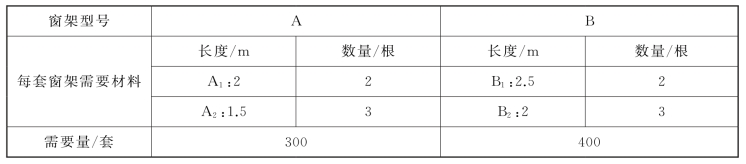
①分析问题,明确目标。下料问题也是已知任务,求费用最小化的问题,但相对复杂,不能像以上例题那样设置决策变量。需要先确定下料方案,如表1-10所示。

表1-10

②变量设置。假设xj为第j种方案使用原材料的根数(j＝1,2,…,10)。(www.xing528.com)

③建立模型。

目标函数:十种方案的下料根数越少越好,即min Z＝x1＋x2＋x3＋x4＋x5＋x6＋x7＋x8＋x9＋x10。

约束条件:必须满足四种规格材料的数量,即

变量取值:满足非负条件,即xj≥0(j＝1,2,…,10)。

综上,模型为:

对于本题有两点需要说明:第一,由于下料方案不同,因此模型结构不是唯一的;第二,变量取值为整数,属于整数规划问题,该问题将在第4章中详细介绍。

(3)运输问题。

【例1-7】某公司从两个产地A1,A2将物品运往三个销地B1,B2,B3,各产地的产量、各销地的销量和各产地运往各销地每件物品的运费如表1-11所示,问:应如何调运才可使总运输费用最小?

表1-11

解:

①分析问题,明确目标。这是已知任务求(确定运输方案),求成本最小化的问题。

②变量设置。由于是多个工厂对应多个销售点,所以变量采用双下标,xij表示第i工厂到第j个销售点的调运量,i＝1,2,j＝1,2,3。

③约束条件。这是一个产销平衡的运输问题,即产量全部用完,销量全部满足。

工厂生产的产品全部用完:

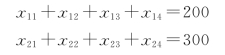
销售点的需求量全部满足:

④非负约束。对于变量xij,若有调运,则变量大于零,若无调运,则变量等于零。

该问题线性规划模型为:

思考:对于本例,若xij小于零,是何含义?