
视频-1.1线性规划问题与模型-1生产计划
(1)生产计划问题。
生产计划问题是已知资源,求利润最大化的典型问题,对于此类问题,通常有如下假设:
①时间假设。生产计划问题是假设在某一计划期内(如一个月)对生产做出的安排。
②损失假设。例如生产(如切割、混合等)过程的损失忽略不计。
③需求假设。生产计划问题一般假设市场需求无限制,即生产的产品可全部卖出。
【例1-1】某工厂在计划期内安排Ⅰ,Ⅱ两种产品的生产,已知生产单位产品所需要的设备台数、两种原材料的消耗量以及利润如表1-2所示,问:如何安排生产才能使利润最大?
表1-2
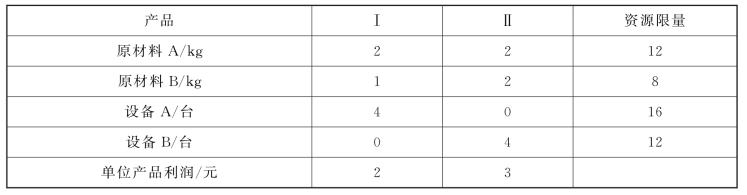
解:
按照运筹学应用步骤,建立该问题的数学模型,过程如下:
①分析问题,明确目标。该问题已知资源,求利润最大。
②建立模型。首先,利润如何表达?根据题意,已知单位产品利润,因此只有确定每种产品的数量,才能确定总利润。为此,设Ⅰ,Ⅱ的产量分别为x1和x2,总利润的表达式为Z=2x1+3x2,求其最大值即为max Z=2x1+3x2。其次,资源消耗了多少?对于本例,资源的使用情况如表1-3所示。
表1-3

生产数量为x1的产品Ⅰ和数量x2的产品Ⅱ所消耗的原材料A为(2x1+2x2)kg,原材料B为(1x1+2x2)kg,设备A为(4x1+0x2)台,设备B为(0x1+4x2)台。由于四种资源的限制量为12,8,16和12,资源限制条件可以表达为:2x1+2x2≤12,1x1+2x2≤8,4x1+0x2≤16,0x1+4x2≤12。最后,对于变量x1和x2,如果生产,则取值大于零,如果不生产,则取值等于零,因此有:x1,x2≥0。
综上,该生产计划问题可用下列数学语言进行描述:

“st..”是英文“subject to”的简写,意思是“使满足、使服从”,即模型(1-1)表示在同时满足条件“2x1+2x2≤12,1x1+2x2≤8,4x1+0x2≤16,0x1+4x2≤12,x1≥0和x2≥0”的基础上求函数“Z=2x1+3x2”的最大值。在模型(1-1)中,含有一般线性规划数学模型的四个要素:
①决策变量:x1为产品Ⅰ的产量,x2为产品Ⅱ的产量,都是需要确定的未知量。
②目标函数:目标函数反映出问题的目标是求利润最大化,即max Z=2x1+3x2。
③约束条件:生产受资源制约,不能超过限制量。因此,有四个资源限制条件:
“原材料A”约束条件数学表达为:2x1+2x2≤12;
“原材料B”约束条件数学表达为:1x1+2x2≤8;
“设备A”约束条件的数学表达为:4x1≤16;
“设备B”约束条件的数学表达为:4x2≤12。
④非负约束:两种产品的产量不能为负值,即x1≥0,x2≥0。
(2)混合配料问题。
【例1-2】某糖果厂要用三种原料A,B,C混合调配出三种不同牌号的糖果产品甲、乙、丙,数据如表1-4所示。问:该如何安排生产,使利润收入为最大?

视频-1.1线性规划问题与模型-2混合配料
表1-4

解:
①分析问题,明确目标。该问题同样是已知资源,求利润最大化问题。因为不同牌号糖果产品中原料的含量有限制,所以不能直接将甲、乙、丙糖果产品的产量设置成决策变量,在这一点上本题与【例1-1】有所不同。
②设置决策变量。由于糖果产品为多种原料混合而成,即成品的数量为各种原料的数量之和,所以可考虑设置原料的数量为决策变量,并且用双下标表示。不妨设xij为生产第j种糖果使用的第i种原料的数量(i=1,2,3;j=1,2,3),如表1-5所示。这样,甲、乙和丙糖果产品的产量分别为:x11+x21+x31,x12+x22+x32和x13+x23+x33,A,B和C三种原料的使用量分别为:x11+x12+x13,x21+x22+x23和x31+x32+x33。
表1-5

③目标函数。利润=收入-成本。
收入:50×(x11+x21+x31)+35×(x12+x22+x32)+25×(x13+x23+x33);
成本:65×(x11+x12+x13)+25×(x21+x22+x23)+35×(x31+x32+x33);
max Z=50×(x11+x21+x31)+35×(x12+x22+x32)+25×(x13+x23+x33)-65×(x11+x12+x13)-25×(x21+x22+x23)-35×(x31+x32+x33)。
④约束条件。约束条件包含三个部分:
第一,资源限量条件:要满足各种原料的限制使用量。
x11+x12+x13≤100
x21+x22+x23≤100
x31+x32+x33≤60
第二,工艺条件:是指不同原料在不同品牌糖果产品中的含量。
x11÷(x11+x21+x31)≥50%
x21÷(x11+x21+x31)≤25%
x12÷(x12+x22+x32)≥25%
x22÷(x12+x22+x32)≤50%
第三,非负条件:是指决策变量的取值范围,若使用原料xij,则取值大于零,若不使用原料xij,则取值等于零,即xij≥0(i=1,2,3;j=1,2,3)。
综上,该线性规划问题模型的一般形式为:(https://www.xing528.com)
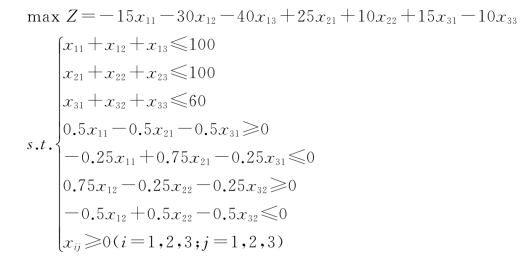
(3)投资策略问题。
【例1-3】某投资公司在第一年年初有100万元资金,每年都有如下的投资方案:第一年(今年)年初投入一笔资金,第二年(明年)年初又继续投入此资金的50%,那么到第三年(后年)年初就可回收第一年年初投入资金的两倍。问:该投资公司如何确定投资策略才能使公司在第六年年初所拥有的资金最多?

视频-1.1线性规划问题与模型-3投资问题1

视频-1.1线性规划问题与模型-4投资问题2
解:
①分析问题,明确目标。投资策略问题也是求目标最大化问题,但是与前面的问题有较大区别。目标函数必须进行递推才能得出,因此需要明确每一年的资金使用情况。
②模型建立。
根据题意,需要建立每一年资金使用情况的等式,即:
追加投资金额+新投资金额+保留资金=可利用的资金总额
因此可设x1为第一年的投资,x2为第一年的保留资金,第一年没有追加投资,则
x1+x2=100
设x3为第二年新的投资,x4为第二年的保留资金,第二年追加投资x1/2,则
(x1/2+x3)+x4=x2
设x5为第三年新的投资,x6为第三年的保留资金,第三年追加投资x3/2,则
(x3/2+x5)+x6=x4+2x1
设x7为第四年新的投资,x8为第四年的保留资金,第四年追加投资x5/2,则
(x5/2+x7)+x8=x6+2x3
根据题意,第五年年初不再进行新的投资,因为这笔投资要到第七年年初才能收回,因此设x9为第五年的保留资金,则
(x7/2+x9)=x8+2x5
到第六年年初,实有资金总额为x9+2x7,根据题意:max Z=2x7+x9,将上述分析结果整理后,可得到最终的模型(1-2),注意模型的一般表达形式。
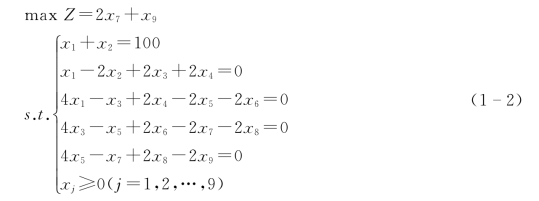
【例1-4】某部门现有资金200万元,今后五年内有以下投资方案:
项目A:从第一年到第五年每年年初都可投资,当年年末能收回本利110%;
项目B:从第一年到第四年每年年初都可投资,次年年末能收回本利125%,但规定每年最大投资额不能超过30万元;
项目C:需在第三年年初投资,第五年年末能收回本利140%,但规定最大投资额不能超过80万元;
项目D:需在第二年年初投资,第五年年末能收回本利155%,但规定最大投资额不能超过100万元。
假设有钱就用于投资,问:如何确定投资方案,才能使该部门在第五年年末拥有资金最多?
解:
由于在不同年份有不同的投资方案可供选择,因此在设置变量的时候应考虑使用双下标,可设xij为第i年年初投入到j项目的资金额,如表1-6所示。
表1-6
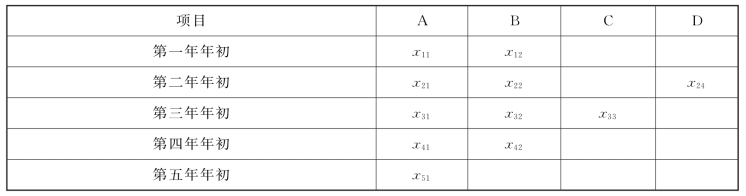
①约束条件。
第一年年初,可投资项目A和B,因此有x11+x12=200。
第二年年初,可投资项目A,B和D,投资额为1.1x11,则x21+x22+x24=1.1x11。
第三年年初,可投资项目A,B和C,投资额为1.1x21+1.25x12,则:x31+x32+x33=1.1x21+1.25x12。
第四年年初,可投资项目A,B,投资额为1.1x31+1.25x22,则x41+x42=1.1x31+1.25x22。
第五年年初,只可投资项目A,投资额为1.1x41+1.25x32,则x51=1.1x41+1.25x32。
②投资限额:x12≤30;x22≤30;x32≤30;x42≤30;x33≤80;x24≤100。
③非负约束:xij≥0(i=1,2,…,5;j=1,2,3,4)。
④目标函数,只需考虑第五年年末的本利和。
项目A:x51→1.1x51;
项目B:x42→1.25x42;
项目C:x33→1.4x33;
项目D:x24→1.55x24。
因此,第五年年末拥有的资金为:
Z=1.1x51+1.25x42+1.4x33+1.55x24
综上,该线性规划问题的模型为:
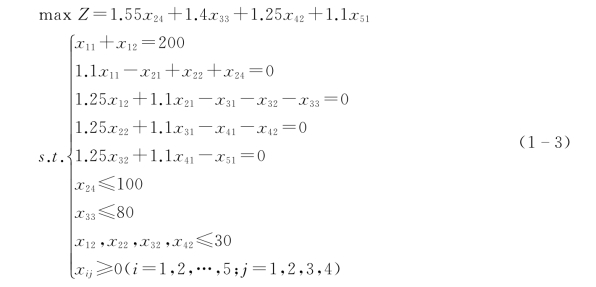
注意本题条件:有钱就会用于投资,即可利用的资金=投资组合所需资金,据此建立约束等式。
需要指出的是,模型(1-3)是该问题模型一般形式的规范表达。
思考:对于【例1-4】,如果项目A,B,C,D的风险系数分别为1,3,4,5.5,该部门应如何确定投资方案,可以在第五年年末拥有资金的本利在330万元基础上的总投资风险系数最小?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




