单位根检验在面板数据分析中的重要性

面板数据模型在回归前需检验数据的平稳性。一些非平稳的经济时间序列往往表现出共同的变化趋势，而这些序列间本身不一定有直接的关联，此时，对这些数据进行回归，尽管有较高的R平方，但其结果是没有任何实际意义的，这种情况称为虚假回归或伪回归。因此，为避免伪回归，确保估计结果的有效性，我们必须对各面板序列的平稳性进行检验，而检验数据平稳性最常用的办法就是单位根检验。所以，在对面板数据进行协整检验与回归分析前须通过单位根检验。

在非平稳的面板数据渐进过程中，Levin Andlin很早就发现这些估计量的极限分布是高斯分布，这些结果也被应用在有异方差的面板数据中，并建立了对面板单位根进行检验的早期版本。后来经过Levin etal.的改进，提出了检验面板单位根的LLC法。Levin etal.指出，该方法允许不同截距和时间趋势，异方差和高阶序列相关，适合于中等维度（时间序列介于25～250之间，截面数介于10～250之间）的面板单位根检验。IM et al.还提出了检验面板单位根的IPS法。Maddala and Wu又提出了Fisher-ADF和Fisher-PP面板单位根检验方法。Breitung发现IPS法对限定性趋势的设定极为敏感，并提出了面板单位根检验的Breitung法。

迄今为止，面板数据单位根检验流行的方法有LLC检验、IPS检验、Fisher-ADF检验、Fisher-PP检验、HadriI检验等。

（一）LLC检验

LLC检验原理是仍采用ADF检验式形式。但使用的却是Δyij和yij的剔出自相关和确定项影响的、标准的代理变量。LLC检验以如下ADF检验式为基础：

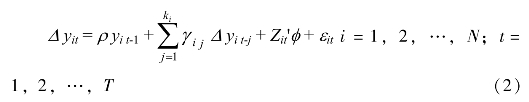
LLC检验的假设为H0：ρ=0（有单位根），H1：ρ<0

（二）IPS（Im-Pesaran-Shin）检验

IPS检验克服了LLC检验的缺陷，允许面板中不同个体（序列）的ρi不同。IPS检验式是

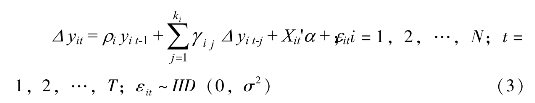
IPS检验假设为

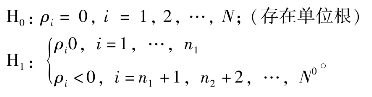
（三）崔仁（In Choi）检验，又称Fisher-ADF检验

崔仁（2001）提出了两种组合Pi值检验统计量。这两种检验方法都是从Fisher原理出发，首先对每个个体进行ADF检验，用ADF统计量所对应的概率Pi的和构造ADF-Fisher X2和ADFChoi Z统计量。原假设H0是存在单位根。在原假设成立条件下，

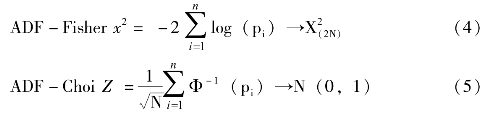
其中Φ-1（·）表示标准正态分布累计函数的倒数。(www.xing528.com)

（四）Hadri检验

Hadri检验原假设是面板中的所有序列都不含有单位根。计算步骤是用原面板数据的退势序列（残差）建立LM统计量。

退势回归是

Yit=α1+α2t+uit

利用上式中的残差计算如下LM统计量：

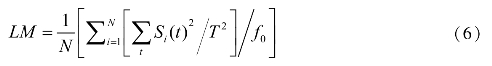
其中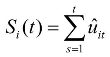是残差累积函数，f0是频率为零时的残差谱密度。

Hadri给出，在一般假定条件下

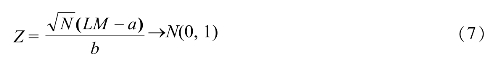
其中a=1/6，b=1/45，LM由（6）式计算。

对于上述几种单位根检验方法，LLC检验在一段时间内应用广泛，但限于同质面板数据且备择假设与实际相距甚远，后面四种针对异质面板数据，其中，IPS检验假设更符现实，不过对非平衡面板数据则无法处理，而Fisher-ADF、Fisher-PP及HADRI检验结果则比较稳定^[38]。因此，为了避免单一方法存在的缺陷，使检验的结果更具有可靠性和稳健性，本文综合选择了LLC检验、IPS检验、Fisher-ADF检验、Fisher-PP检验方法对变量进行平稳性检验，检验结果见表7-7。

表7-7　面板数据单位根检验结果

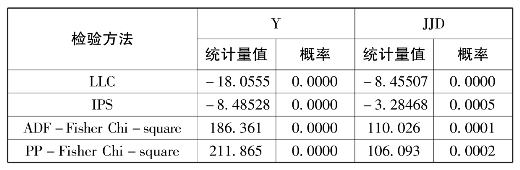
注：LLC、IPS、Fisher-ADF、Fisher-PP检验的原假设为存在单位根。

从表7-7面板数据单位根检验结果可以看出，无论是应用LLC检验、IPS检验，还是Fisher-ADF检验以及Fisher-PP检验，所有变量都显著地拒绝了其存在单位根的原假设，同为零阶单整，可以推断模型（1）中的数据是平稳的。因此，可以进行协整检验及回归分析。