开发区政策与企业全要素生产率的PSM分析

1.开发区政策的倾向分析

为了控制样本选择偏差，本章采用倾向评分匹配（Propensity Score Matching，PSM）方法评估并验证开发区的政策效应，以期得到更为一致的估计结果，这种方法近似自然实验。检验开发区政策的企业全要素生产率效应，将样本分成控制组和处理组两个组。其中，控制组是始终没有进入开发区和进入开发区之前的企业，处理组是开发区成立之后进入开发区的企业。通过倾向评分匹配，可以得到一个倾向分值（PS），通过这个PS值，可以在多维度范围内匹配处理组和控制组的企业样本，然后计算有开发区政策支持的企业的平均处理效应（ATT）。

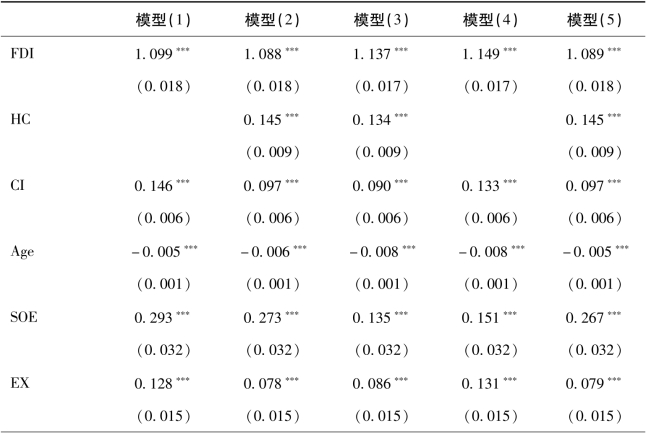
在进行倾向评分匹配分析之前，首先是要估计倾向分值，需要确定可能影响企业是否选择进入开发区的“协变量”组。这一步必须尽可能地保证“协变量”组的准确性，以保证可忽略性假设得到满足。当然，如果选择不当，可忽略性假定将得不到满足，就可能引起偏差。本章使用Logit模型估计开发区政策与“协变量”的相关性，能够确定更恰当的“协变量”组。选择了八个可能影响企业是否进入开发区以及企业TFP的“协变量”，包括外资参与程度、人力资本水平、资本密集程度、企业年龄、行业垄断程度以及出口企业、创新型企业和国有企业哑变量，并通过逐步回归法确定用以控制地区差异、行业差异和年度宏观经济环境的虚拟变量。表6-8为开发区政策的Logit模型估计结果。从模型的估计结果来看，本章确定使用模型（5）的协变量组来估计PS值。估计结果显示，外资参与程度越高、人力资本水平越高、资本密集度越大、企业年龄越大、行业垄断程度越小，越倾向于进入开发区；相比而言，出口企业、国有企业、非创新型企业更倾向于进入开发区。

表6-8　开发区政策的Logit模型估计结果

续　表

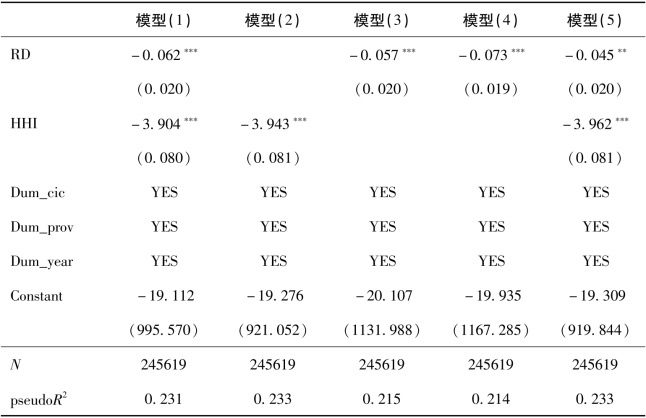
注：圆括号内为标准误，*、**、***分别表示在10%、5%、1%的水平上显著。模型（1）-（5）均是采用逐步回归的方法，保留会显著影响开发区政策哑变量的协变量。

2.样本匹配结果

为了使倾向得分估计得更准确，就必须使“协变量”在匹配后的处理组和控制组之间分布较为均匀，即数据平衡（data balancing）。表6-9为主要协变量的平衡性检验结果。平衡性检验主要是考察变量的“标准化偏差”（standardized bias），其表达式为：

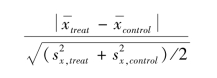
其中，分别表示处理组和控制组协变量x的样本方差。一般认为，如果此标准化偏差不超过10%，则说明得到的倾向得分是可靠的。平衡性检验结果显示，除了行业垄断程度的标准化偏差超过5%，其他协变量的标准化偏差均小于5%；匹配后外资参与程度、出口企业、企业年龄、资本密集程度、创新型企业和国有企业的标准化偏差分别为1.6%、0.5%、2.4%、4.6%、1.3%和2.4%。所以，可以认为匹配后的处理组和控制组通过了平衡性检验。

表6-9　主要协变量的平衡性检验结果

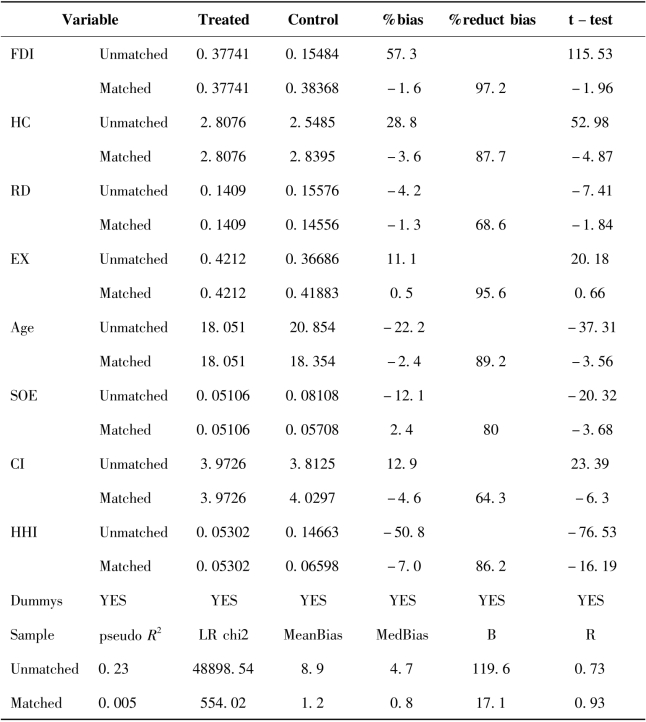
注：if B＞25%，R outside［0.5；2］。

本章是基于最近邻匹配原理，将处理组和控制组的企业样本进行匹配，并对匹配后的样本进行差异分析，以期得到开发区政策参与企业的平均处理效应（ATT）。图6-5为控制组和处理组匹配前后的核密度函数分布图。从图中可以清晰地看出，匹配前处理组和控制组存在显著差异，而匹配后处理组和控制组的核密度函数分布图就变得非常接近了，所有企业均在共同取值范围内（common suport），说明匹配效果较好。匹配后两组样本变量的特征非常接近，已经很难通过协变量来区分哪些企业倾向于进入开发区，哪些企业不倾向于进入开发区。匹配后的样本可以近似认为是一种自然实验，所以如果没有匹配就直接对处理组和控制组进行差异分析，得到的结果可能存在偏误。

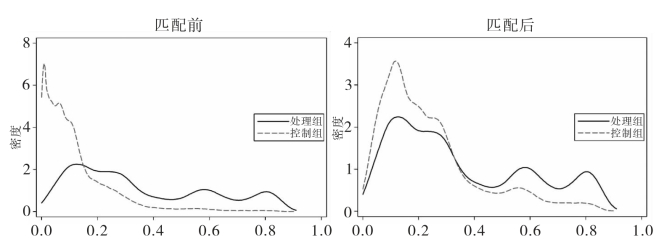
图6-5　匹配前后处理组与控制组的核密度图

3.开发区政策的生产率效应分析

表6-10为匹配前后全样本开发区政策的平均处理效应（ATT）。结果显示，基于OP法、LP法和GMM法三种方法估计的TFP的ATT均显著为正，说明开发区政策可以有效促进企业的全要素生产率的提升。其中，匹配前开发区政策下TFP的平均处理效应为0.256，匹配后平均处理效应降为0.029（基于OP法估计的TFP值）。由于匹配前得到的ATT是没有控制任何变量时，开发区政策的平均处理效应，所以无法直接说明OLS估计方法是否会导致开发区政策效应被高估。但前文的基准分析与PSM分析控制了相同的控制变量，所以可以根据前文基准回归结果进行比较，全样本OLS估计方法的开发区政策平均处理效应为0.026，固定效应估计的开发区政策效应为0.031。普通面板模型估计方法与PSM分析方法所得的开发区政策平均处理效应差异并不大，说明样本“自选择性误差”问题并不严重。(www.xing528.com)

表6-10　全样本下开发区政策的平均处理效应（最近邻匹配原则）

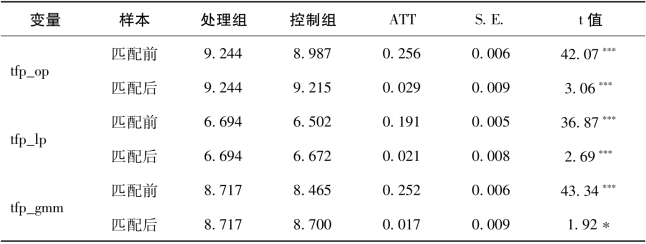
注：匹配前表示样本还没经过处理组合控制组的匹配；匹配后表示控制协变量后，处理组与控制组已经没有显著差异，无法根据协变量进行区分，企业是否有开发区政策支持；*、**、***分别表示在10%、5%、1%的显著性水平。

为了更为细致地探讨开发区政策对企业生产率的影响，进一步根据企业所有制对全样本企业进行分类，将全样本分为国有企业和非国有企业两个分样本，并比较开发区政策的平均处理效应在国有企业和非国有企业之间的差异。表6-11为开发区政策的ATT处理效应在国有企业和非国有企业之间差异结果。估计结果显示，开发区政策仅对非国有企业有效，其开发区政策的平均处理效应为0.026，在1%的水平上显著。

表6-11　开发区政策的平均处理效应：国有与非国有企业的差异

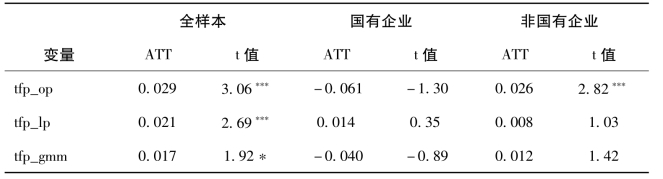
注：*、**、***分别表示在10%、5%、1%的显著性水平；ATT表示处理组和控制组的平均处理效应。

进一步比较了不同区域内开发区政策的平均处理效应的空间差异（见表6-12），发现开发区政策的生产率效应存在显著的空间差异；沿海地区和内陆地区的开发区政策均能够显著提升企业TFP，而沿边地区的开发区政策却显著阻碍了企业TFP的提升。沿边地区远离国内大市场，且自身市场规模较小，交通基础设施薄弱，产业配套能力差，没有规模经济支撑的大规模开发区建设可能造成严重的“空间错配”问题，无法有效地提升企业全要素生产率。陆铭教授将这种“空间错配”现象解释为：人口流出地得到越来越多建设用地指标和土地供应，而人口流入地反而成为土地供应相对不足的地方，即土地受到了供给端的限制。要使开发区建设作用得到有效发挥就必须有规模经济、集聚经济、人力资本、基础设施条件以及足够的产业配套能力作为支撑。因此，是市场规模约束导致了沿边地区开发区政策不仅无法提升企业全要素生产率，甚至还可能产生阻碍作用。

表6-12　开发区政策的平均处理效应：空间差异

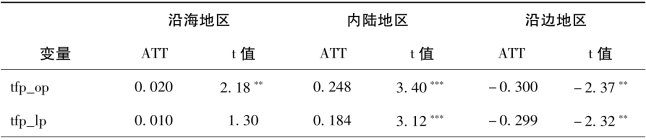
续　表

注：*、**、***分别表示在10%、5%、1%的显著性水平；ATT表示处理组和控制组的平均处理效应。

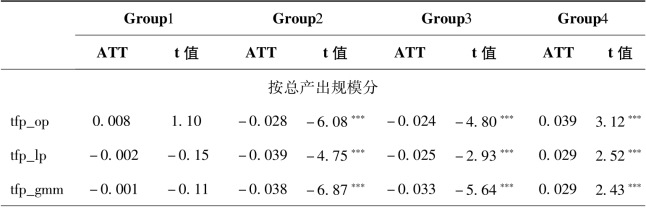
本章进一步将样本按企业总产出和出口交货值从小到大分成4个小组。表6-13为开发区政策下TFP的平均处理效应在不同国内市场规模和国外市场规模下的差异，其中表的上半部分是按总产出分的ATT处理效应估计结果，下半部分是按出口规模分的ATT处理效应估计结果。估计结果显示，随着国内市场规模和国外市场规模的扩大，开发区政策下的企业生产率效率开始提升。在企业市场规模较小的情况下，开发区政策不仅无法提升企业生产率，还阻碍企业TFP的提升，当企业市场规模足够大时，开发区政策能够显著提升企业TFP。同时还可以得出出口规模与企业生产率之间的“U”型关系：当出口规模大于75%时，出口企业的TFP的平均处理效应最大；当出口规模介于0和25%时，出口企业的TFP的平均处理效应较低；而当出口规模在25%和75%之间时，出口企业的TFP的平均处理效应并不显著。

表6-13　开发区政策的平均处理效应：规模差异

续　表

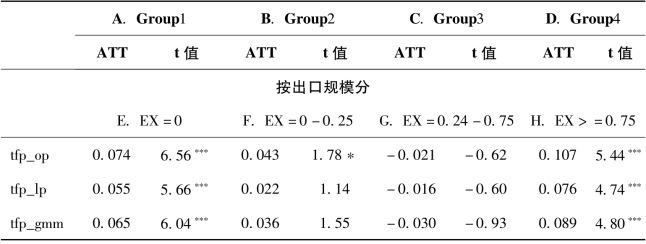
注：*、**、***分别表示在10%、5%、1%的显著性水平；ATT表示处理组和控制组的平均处理效应；EX表示企业出口密度规模（国外市场规模），即企业出口交货值占总产出的比。