企业全要素生产率的演进分析

1.全要素生产率的估计方法

全要素生产率（TFP）是指总产出中不能由要素投入解释的那部分剩余，用以反映投入减去产出的总体效率。也有很多研究用企业TFP来反映企业的技术水平，但这并不全面，TFP与企业内部管理及制度环境等有关。本章用全要素生产率反映企业生产率，是促进生产活动空间集聚的重要因素。最早全要素生产率的估算源于索洛的生产函数，一般被用于宏观经济层面的研究。随着数据的可获得性，逐渐发展到微观层面。现有文献中对企业全要素生产率测算主要有OLS法、固定效应估计技术、OP法（Olley and Pakes，1996）、LP法（Levinsohn and Petrin，2003）和GMM法（Blundell and Bond，1998）五种，其中OP法、LP法和GMM法对估计偏误进行了处理，使用频率较高。对全要素生产率的估计首先是基于对生产函数的设定，其次才是对生产函数的估计。最常用的生产函数形式是柯布道格拉斯（C-D）生产函数，结构简单，使用频率最高，表达式为：

其中，Y、L和K分别表示产出、劳动和资本，A就是通常所说的全要素生产率（TFP），能够使得生产函数外生移动。C-D函数的线性对数函数表达式为：

其中，全要素生产率即是残差项的估计值，但如果简单应用线性估计方法（OLS估计方法），可能会产生同时性偏差和样本选择性偏差。其中同时性问题最为突出，即企业生产率提升在当期被决策者观测到，并据此调整生产要素投入组合以达到利润最大化，那么就会导致这一部分残差与回归项相关，使得OLS的估计结果产生偏误。这一偏误的表现形式被Marschak和Andrews（1944）描述为以下形式：

其中，θit作为可被观测到并影响当期决策的要素投入组合的那部分残差项，εit表示不可观察的技术、管理、政策等的冲击和测量误差形成的残差项。样本选择性偏误问题主要是由企业资本存量、生产率冲击与企业下一期是否退出市场之间的相关性所导致。一般而言，资本存量较大的企业在受到低生产率冲击时，较不轻易退出市场，这就会使得资本项的估计系数被低估。为了解决这些估计偏误问题，提出了对TFP的多种估计方法，即前文所述的FE法、OP法、LP法和GMM法等。

（1）FE法。固定效应估计方法是在（6.2）式的基础上引入企业个体特征的虚拟变量，从而解决θit带来不随时间而变的遗漏变量问题，但无法解决不随个体而变的遗漏变量问题。在本章估计中，不管是OLS法还是FE法，均同时控制了年度、省份及行业的虚拟变量，在最大程度上控制了模型不随时间而变和不随个体而变的遗漏变量所引致的内生性问题。

（2）OP法。OP法是Olley和Pakes（1996）提出的，是一种半参数估计方法。该方法假定决策者根据当期企业生产率做出了调整，用企业当期投资作为不可观测生产率冲击的代理变量解决同时性偏误。本章主要以OP法为基础进行实证研究，同时在稳健性研究中尝试检验不同估计方法可能带来差异。OP法强调企业当期投资与生产率冲击预期和资本存量有关，那么最优投资函数可以表示为：iit=i（θit，kit），即当期预期的生产率越高，那么当期的投资额也越高。求得该最优投资函数的反函数为：

将（6.4）式带入（6.3）式得到新的生产函数方程为：

令φit=β·kit+h（iit，kit），进一步整理生产函数（6.5）式得到：

其中，前一项表示劳动贡献，后一项表示资本贡献。对（6.6）式进行估计，就可以得到劳动项的一致无偏估计系数。然后用估计系数来拟合φit的估计值。假定h（iit，kit）=i-1（θit-1，kit-1），令Vit=yit-~α·lit，结合（6.4）式可以得到以下估计方程：

(www.xing528.com)

其中，（6.7）式包含了资本存量的滞后期和当期值，使得估计变得复杂得多。为了得到有效估计值，这就要求非线性的最小二乘估计。当（6.7）式被估计完成，可以利用该结果来拟合（6.1）式，获得残差项的对数值，即TFP的对数值。

（3）LP法。OP法要求当期投资额与总产出始终保持单调关系，才能得到TFP的一致估计值。这就使得投资额为0的企业样本无法被估计。然而，在实际生活中，确实存在企业在有些年份投资额为0的情况，而在OP法估计中，这些样本将被剔除。Levinsohn和Petrin（2003）针对这一问题提出新的估计方法，即LP法。LP法使用中间投入品作为生产率冲击的代理变量。LP法和OP法都属于半参数的估计方法，均处理了前文所说的估计偏误问题。

（4）GMM法。GMM法是Blundell和Bond（1998）提出的一种广义矩估计法，通过加入工具变量来解决模型中的内生性问题。其中，工具变量为被解释变量的滞后值，由前期决定，从而与当期的生产效率冲击无关。GMM估计方法要求样本具有足够长的时间跨度，以满足大量的差分和滞后值处理，来构造合适的工具变量。本章对中国工业企业的TFP估计参照鲁晓东和连玉君（2012［132］）对中国工业企业全要素生产率的估计方法，分别用OLS法、FE法、OP法、LP法和GMM法五种方法进行估计。

2.全要素生产率的演进规律

本章中对工业企业TFP的估算得到的估计值均在300万以上，绘制了不同方法估计得到的TFP值的核密度函数图，叠加到一起进行比较分析TFP的分布特征和动态变化（如图6-1）。五种方法得到的TFP值均在偏度—峰度检验^[1]中拒绝了分布的正态性假设^[2]。OLS法和FE法两种方法估计的TFP值得到的核密度函数基本重合，TFP均值最小，均值为5.42；而OP方法估计的TFP均值最大，达到8.357，其他依次为GMM法和LP法，TFP均值分别为7.908和6.152。虽然这五种方法估计得到TFP核密度函数图形状相似，但在统计量对比中仍存在一定差异。首先，OP法和GMM法两种方法估计的TFP值得核函数图的偏度均大于0，呈正偏态分布，偏度值分别为0.098和0.049；而其他三种方法估计的TFP值得偏度均小于0，呈负偏态分布；其中LP方法估计的TFP偏度绝对值最大，达到了0.272，OLS法和FE法两种方法估计的TFP偏度绝对值分别为0.266和0.270，这三种方法下有更多的值落在众数的左侧。其次，OLS方法和FE方法估计的TFP值的峰度值最大，达到5.002，说明该分布最为陡峭；而GMM法、LP法和OP法三种方法估计的TFP值的峰度值分别为4.868、4.831和4.786，其中OP方法估计的TFP值分布最为平缓。因此，本章后续的研究以OP法估计的TFP值为基础展开，但在稳健性检验中同时也参考LP法和GMM法估计的TFP值。

图6-1　中国工业企业的全要素生产率（TFP）的核密度图

此外，表6-2列出了五种方法估计的TFP估计值，为了考察它们与劳动和资本两种投入要素生产率的相关性，还在矩阵中同时加入劳动生产率和资本生产率两个指标。参数估计方法和非参数估计方法的TFP估计结果之间的相关性很高，而TFP与资本生产率及劳动生产率的相关性却很低。不同估计方法得到的TFP值及其与资本和劳动要素生产率的相关性说明工业企业生产率提升过程中资本和劳动单要素投入的作用并不大，重要的是其他要素投入的作用。

表6-2　各种方法下的TFP估计值的相关系数矩阵

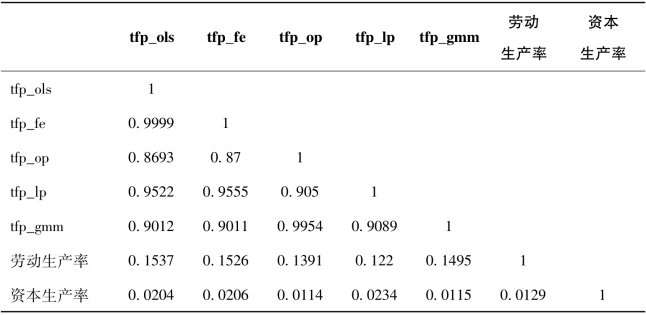
图6-2呈现了2001—2013年中国工业企业不同方法估计的TFP的变化趋势。五种方法估计的TFP值呈现基本较为一致的趋势：2001—2009年间，中国工业企业TFP稳步上升，2010年稍有回落，这可能是源于国际金融危机带来的滞后效应，2011—2013年又出现TFP回升的现状。从图中不难看出，OLS法和FE法估计的TFP值最小，OP法估计的TFP值最大；OLS法与FE法估计的TFP值的趋势线重合，OP法和GMM法两种方法估计的TFP值的趋势基本一致。

图6-2　2001—2013年中国工业企业TFP的变化趋势

在综合分析中国工业企业TFP变化趋势后，进一步对企业TFP进行分区域评价。图6-3呈现了中国沿海、沿边及内陆地区工业企业TFP（OP）的变化趋势。基本表现为沿海地区工业企业具有相对较高的TFP水平，高于内陆及沿边地区；沿边地区和内陆地区工业企业TFP水平相对较低，均低于全国平均水平。此外，沿海、沿边和内陆地区三个区域的工业企业TFP水平随着时间的推移呈现收敛趋势（谢千里等，2008［133］）；内陆地区的TFP受经济环境冲击的敏感度最高，其次是沿边地区，而沿海地区受经济冲击的影响则相对较小。这也说明了前文所述的单纯依靠线性OLS估计TFP可能会产生的估计偏误问题。

图6-3　2001—2013年沿海、沿边及内陆地区企业TFP（OP）的变化趋势