稳定性分析的重要性与实践

1.突破点

对称均衡分布被打破时的贸易自由度临界值被称为突破点，表达式为：。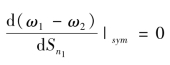

如果在对称分布的长期均衡点，实际工资差异对Sn1 的导数为负，经济系统内存在负反馈机制，对称分布是稳定的；如果该导数为正，则经济系统存在正反馈机制，对称分布不稳定；当该导数等于0时，则达到对称分布被打破的临界点。因此，先假设经济体处于对称分布的长期均衡点，即Sn1 =Sn2 =0.3，Sn0 =0.4，w0=w1=w2=1；然后，根据长期均衡方程组，应用Mablab14.0a软件对边缘地区产业份额Sn1求导，得到ω1-ω2与Sn1的一阶导数；最后，模拟区际贸易自由度θ、国际贸易自由度φ与ω1-ω2和Sn1的一阶导数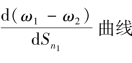^[4]。当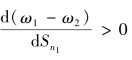时，对称均衡不稳定；当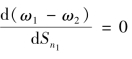时，对称均衡分布是稳定的；当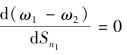时，图2-8标出的φ（B）和θ（B）分别为突破点对应的国际贸易自由度和区际贸易自由度。从图2-8可看出，随着区际交易成本的降低，对称分布被打破的临界点向左移动，突破点的国际贸易自由度降低；同理，随着国际贸易成本的降低，对称均衡的突破点向左移动，突破点所需的区际贸易自由度逐渐降低。

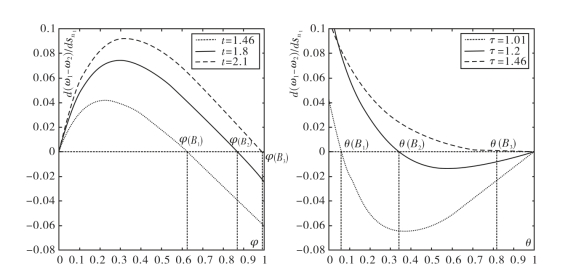
图2-8　突破点

2.支撑点(www.xing528.com)

集聚一旦形成，就会持续存在，当已形成的集聚无法再持续的贸易自由度临界值被称为持续点。假设经济体处于中心—外围的长期均衡结构，模拟维持这种中心—外围的支撑点（如图2-9所示）；左图横坐标为区际贸易自由度θ，右图横坐标为国际贸易自由度φ，图中标出的φ（S）和θ（S）分别为支撑点对应的国际贸易自由度和区际贸易自由度。当ω1-ω2 ＞0时，核心—边缘结构是稳定的；而ω1-ω2 ＜0时，核心—边缘结构会被打破，最终形成稳定的对称均衡结构；当ω1-ω2 =0时，是维持中心—外围结构的最低贸易自由度。从图2-9可以看出，随着国际贸易成本的降低，维持中心-外围结构的区际贸易自由度取值范围逐渐增大；然而，随着区际交易成本的降低，支撑中心—外围结构的最低国际贸易自由度均衡点向右移动，最低国际贸易自由度增加。

图2-9　支撑点

根据对模型稳定性分析的结果得到如下命题：

命题6：区域经济的空间结构存在惯性，即存在明显企业区位的“锁定效应”。