短期均衡下工业品价格与消费者效用水平的关系分析

1.消费者行为

假设所有消费者使用相同的效应函数，即每个消费者的偏好都相同。为不失一般性，假设消费者效用函数由两个层次构成。第一个层次是消费者将总支出用于农产品和制成品消费时所获得的效用，是不同支出比例的农产品和制成品构成的柯布道格拉斯效用函数。第二层效用函数是一系列差异化的制成品消费组合构成的不变替代弹性效用函数。因此，得到代表性消费者的效用函数形式如下：

其中，CM 表示消费者对差异化制成品组合的消费，CA表示消费者对同质型的农产品的消费，μ表述制成品支出份额。第二层效用函数中ρ表示消费者多样性偏好，ρ→0表示消费者多样化偏好强度越强，ρ→1表示消费者多样化偏好强度越弱，σ表示不变替代弹性效用函数中两种差异化制成品间的替代弹性。这里的nw表示整个经济体中差异化工业品的种类，即nw =n0+n1+n2，n0、n1和n2分别表示国外地区、沿边地区和内陆地区企业生产的差异化工业品总数。因为前面假设每个企业只生产一种差异化工业品，所以nw 也表示整个经济体中企业总数，同理，n0、n1和n2分别表示国外地区、沿边地区和内陆地区企业数量。

消费者行为要解决的是均衡时消费者效用最大化问题，设定消费者预算约束条件为：

其中，I为消费者总支出，这里假设消费者将所有收入在当期支出，所以总支出等于总收入。pA表示农产品价格，pi表示第i种差异化工业品的价格。

消费者效用最大化来自于两个方面，一方面是最小化工业品集合CM 的支出成本；另一方面是确定农产品和工业品之间消费比例，使得效用达到最大化。所以，第一步，确定消费者对第i种工业品的消费量ci，使得其对工业品集合CM的支出最小，即：

代入成本最小化约束式中，得到消费者需求函数

其中，PM 表示工业品价格指数。可以看出，工业品价格指数对工业品种类的敏感程度取决于不同种类工业品之间的替代弹性σ（或消费者多样化的偏好强度ρ）^[2]，σ越小，产品种类增加导致工业品价格指数下降程度越大。

第二步是确定消费者在农产品和工业品之间消费组合，以达到总效用的最大化，即：

最大化的解，可以写成：

代入前面消费者需求函数，得到消费者需求函数的最终表达式为：

由于没有储蓄假定，消费者收入等于支出，即I=E，所以消费者需求函数也可以表达为：

最后，通过间接效用函数得到全部消费品的价格指数表达式。间接效用函数表达式为：

所以，可以得到全部消费品价格指数为。假设消费者的收入仅来自于工资收入w，那么消费者的实际工资ω就等于名义工资收入除以全部消费者价格指数，即ω=w/G（2.13）。

从式（2.10）和式（2.11）可以看出，价格指数G会因为工业品种类n的增加而下降，消费者效用水平也会随着提高。但是产品种类增加，即新产品进入市场，会增加产品市场竞争强度，导致消费者对原有各种工业品的需求曲线向下移动，并使得这些产品的销售量下降。

2.生产者行为

（1）农业部门

完全竞争的农业部门，假设在区际贸易和国际贸易中均不存在运输成本，所以三个地区的农产品价格相同。假设两国的农业劳动力禀赋相同，其中国内农民在国内两地区均匀分布，分别用L0、L1、L2和Lw 表示国外地区、国内沿边地区和内陆地区以及整个经济系统的农业劳动力禀赋，则Lw =L+L0，L=L0。

根据前文消费者的需求函数，沿边地区、内陆地区和国外地区对农产品的需求函数分别可以表达为：

其中，E1、E2、E0分别表示沿边地区、内陆地区和国外地区的总支出。一方面，整个经济体的农业劳动力禀赋Lw，而生产一单位农产品需要aA单位农业劳动力，所以农业总产出就等于Lw/aA。另一方面，经济系统用于农产品的支出份额为（1-μ）Ew，而同质型农产品价格pA，所以消费能够消费的农产品总量就等于（1-μ）Ew/pA。所以，均衡时农产品市场出清条件为：

（2）工业部门

在垄断竞争市场结构下，规模报酬递增的工业部门生产的是差异化工业品。假定每个企业使用相同成本函数，设定单个企业的成本函数为：(www.xing528.com)

企业生产1单位工业品的固定投入为F单位工业劳动力，可变投入为am 单位劳动力，w为工人工资水平，x为工业品产出量。

a.产品定价及生产活动空间分布

D-S垄断竞争框架下的工业企业，规模均较小，企业无法进行差别定价。前面假设每个企业都生产一种差异化工业品，因为有许多潜在厂商进入，所以企业均采取边际成本不变的加成定价，并且均衡时每个厂商的利润为零。所以，构建生产第i种差异化产品的企业利润函数为：

其中，E为整个经济系统的总支出，令k=μE/P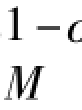σ ，对于第i种产品需求而言，k是常数。所以，利润最大化下第i种产品的价格为：

将产品价格代入利润函数，可以得到均衡时企业的产出量为：

不难看出，均衡时企业的产品价格和产出量均相同，与产品种类无关。式（2.22）说明均衡时每个地区生产一种工业品需要工业劳动力相同，为σF。假设经济体拥有工业劳动力总量为Hw，那么整个经济系统的工业品种类总数就等于工业劳动力禀赋除以一种差异化工业品所需的劳动力数量，即nw =Hw/σF。因为每个企业只生产一种差异化工业品，所以工业品种类等于企业数量。那么，均衡时沿边地区、内陆地区和国外地区企业数量分别为：

其中，H1、H2、H0分别表示沿边地区、内陆地区和国外地区企业的工业劳动力禀赋。上式的产品价格为企业在当地的售价，但如果销售到其他市场，企业会通过更高的售价来弥补产品在运输成本。所以，沿边地区企业在沿边、内陆和国外市场的售价分别为：

同样，内陆地区企业在当地、沿边和国外市场售价分别为：

同理，国外地区企业在当地、沿边和内地市场售价分别为：

b.企业区位和集聚的条件

劳动力作为厂商的唯一投入要素，劳动力流动意味着企业区位的变化。实际工资水平ω的高低决定了一个地区工人禀赋。工人实际工资水平等于工人名义工资水平除以全部消费品价格指数。因为均衡时企业的全部收益用于支付工人工资，为σFw。所以，沿边、内陆和国外地区的企业支付给工人的工资总量分别为σFw1、 σFw2和σFw0。

在市场出清条件下，沿边地区的企业收益为R1 =p1 x1，x1为企业的产出量，p1为产品的出厂价格（等于当地售价）。市场出清时企业所有的产出会在沿边地区、内陆地区或国外地区全部销售出去，即x1=c11+tc12+τc10。其中，c11、c12、c10分别表示沿边地区企业产品在沿边地区、内陆地区或国外地区市场的销售量，因为存在区域间运输成本，所以实际供应量分别为c11、tc12、τc10。均衡时沿边地区企业收益为R1 =p1（c11+tc12+τc10）=p1 c11+p12 c12+p10 c10。

其中，PM 1、PM2和PM0分别表示沿边地区、内陆地区和国外地区的工业品价格指数，令θ=（t）1-σ，φ=（τ）1-σ， φ、δ分别表示区际贸易自由度和国际贸易自由度。根据定义：

进而可以得到工人的实际工资水平的表达式：

c.企业的相对市场规模

沿边地区的总支出（总收入）水平：E1 =wL1 L1+w1 H1=wL1 SL1 Lw+w1 SH 1 Hw；

内陆地区的总支出（总收入）水平：E2 =wL2 L2+w2 H2；

国外地区的总支出（总收入）水平：E0 =wL0 L0+w0 H0；

加总得到整个经济系统的总支出水平：Ew =wL Lw+w1 H1+w2 H2+w0 H0；其中，w1 H1+w2 H2+w0 H0 =μEw；所以wL Lw =（1-μ）Ew。

从式（2.48）-（2.50）可以看出，各地区相对市场规模等于该地区农业劳动力禀赋和工业劳动力禀赋的加权平均值，权重为工人工资和农民工资；相对工业劳动力份额变化会导致相对市场规模的同向变动，其中相对工业劳动力份额变化又意味着企业空间分布变化。