应用时间回归法进行负荷预测

回归分析是一种数理统计的方法。它通过对事物因果关系的分析，找出其变化规律，建立数学模型，然后应用数学模型进行预测分析。所以它比各种单项预测法以及综合预测法中电力弹性系数法、时间序列预测法等具有更高的预见性和可靠性，近几年来在电力预测分析中应用较为广泛。

1.常用的数学模型

应用回归分析法预测的关键在于建立数学模型。事物之间相关关系呈线性相关时称为线性回归；反之，事物之间相关关系不呈线性相关时，称为非线性回归。预测中常用的回归数学模型可分为：

表9-4　各分区负荷密度表

2.应用线性回归预测电量

为了建立回归方程，必须有足够数量的统计数据，表9-5中是1978～1991年某县用电量得统计数据。将这些数据描绘在以电量Y为纵标、以t为横标的直角坐标系中，如图9-1所示。

表9-5　各年电量表

实验数据Yt可用下述方程式描述

式中　Yt——第i年电量；

t——时间；

ε——误差，其可正、可负。

图9-1　线性回归

今若建立一回归方程

式中　Yt——预测目标；

a、b——回归系数；

t——时间周期次第数，t=1，2，3，4，…（可为年、月、周）。

来代替上面的方程，并使其误差的平方和最小，即

最小，这就是最小二乘法原理。因此，最小二乘法是用系数a，b来估计试验方程系数。α、β，A的方法。用这种方法求出的直线Yt=a+bt是这样一条直线，这条直线与各试验点（t，Yt）的偏离是一切直线中最小者。

因为

（1）回归系数的确定。

由上述方程可以看出，其中，Yt、t是已知的试验数据，而a、b是待求系数，所以M为a、b的二元函数，为使M达极小值，只要求M对a、b的偏导数、并令其为0，即

微分后，得

由以上方程可得

由上面方程的第一方程可以解出

式中　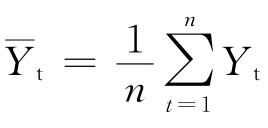——预测期内各年电量的平均值；

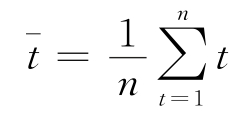——预测期年份的平均值。

采用行列方法，求出系数b的表达式

注意到

于是上式可以写成

利用公式可计算回归方程Yt=a+bt的系数b，然后再计算系数a。

根据表4-5中的数据，利用公式求解方法如下：

于是则有

系数b为

系数a为(www.xing528.com)

所以预测方程公式为

一般预测模型为

但有时为了能直观地看出今后几年的预测值，也可以将预测模型改变为

式中　T——距当前最近或很近的时间周期，例如1992年；

l——预测周期与周期T相隔的周期数；

Yt+1——第T+l周期的预测值；

aT——T周期预测目标的估计值；

bT——回归方程的斜率，bT=b。

（2）电量的预测。

将有关数据代入公式aT=a+bT中，因T=15，所以

故所求预测模型改为

预测计算：

时间回归的预测计算，不必须测自变量，而只需确定预测周期的次第数，对周期t取值法是第一个周期的t=1，第二个周期的t=2，以后各周期依次类推。这种取值方法与其他取值法比较有计算工作量小，直观和不易出错的优点。只要将其值代入公式中即可。

现根据预测模型式，作某县2005年前各年用电量预测计算，见表9-6。

从表9-6中可知Y1992，Y1993和Y1994值都小于Y1991已知值，故需修正，即将回归线向上平行移动到穿过Y1991年点，这表明今后各年该县用电量将以1991年用电量为基础，每年递增回归方程斜率的数值1034.6万kW·h。

经修正后的预测模型的截距a′可由下式算出

修正

修正后的预测模型为

预测结果列于表9-7。

表9-6　2005年以前各年电量

表9-7　电量预测结果

应用时间回归作预测，在求得回归方程之后，仍要做相关系数的检验，但时间回归法的相关检验，t检验以及置信区间计算方法，都与因果分析线性回归法相同，只需将后者的自变量x改为时间周期次数t即可，故此不作赘述。本例相关系数检验得R=0.895。按置信度为95％。N=14，查相关系数表得R=0.532。0.895>0.532，相关检验通过，可按预测模型进行预测计算，即回归方程成立。

（3）总结时间回归法的预测步骤。

1）确定预测目标。

2）收集预测目标的统计数据和有关信息。

3）画数据的散点图，并处理数据。

4）计算回归系数，建立回归方程，画出回归线。

5）进行相关检验和t检验等。

6）计算预测值。

7）计算预测值置信区间。

8）对预测值进行综合分析，并确定预测结果。

9）画预测发展线。