保留价格和物有所值百分比是什么？

（1）保留价格是指顾客在购买某商品时所愿意支付的最高价格。由此引申出来的消费者剩余，指的是顾客实际购买价格与保留价格之间的差价。保留价格在营销人员评估定价和顾客价值时非常有用。特别是当其他数据不可得时，保留价格为评估产品的需求功效提供了基础，而且还能为营销者提供定价界限方面的参考。

例如，顾客A因为非常喜欢吃牛肉丸，所以愿意花40元买一袋汕头牛肉丸，而实际上，一袋汕头牛肉丸的价格是35元，因此，保留价格为40元，而消费者剩余为5元。

（2）保留价格的实际测量相对困难，可以采取以下两种手段来获取这个计量信息：

1）第二价格密封拍卖。运用这个手段的理论基础是拍卖理论，也就是在诸如此类的拍卖中竞拍已知价值的商品时，个体都有以自身保留价格竞标的倾向。因此，可以设计模拟拍卖过程的调查方法。

2）联合分析。这个手段是指根据顾客的可能需要设定相关的属性，并让顾客按自己的意愿来作出权衡。但实际上，其操作非常困难，因此常常会采用物有所值百分比。

所谓物有价值百分比，是指认为某产品在特定价格的情况下是“物有所值”的顾客比例。换言之，就是这些比例的顾客真正购买到的产品价格，低于或等于他们的保留价格。

（3）用线性函数表示随着保留价格累积而得到的价格-销量变化，表示为Y=mx+b，其中m是直线的斜率，b是Y轴上的截距，如图9-1所示。

其中，保留价格最大值为销量等于零时的最低价格；愿意购买最大值为当产品价格为零时，顾客会“购买”的数量。

以上的线性函数主要有两种应用：

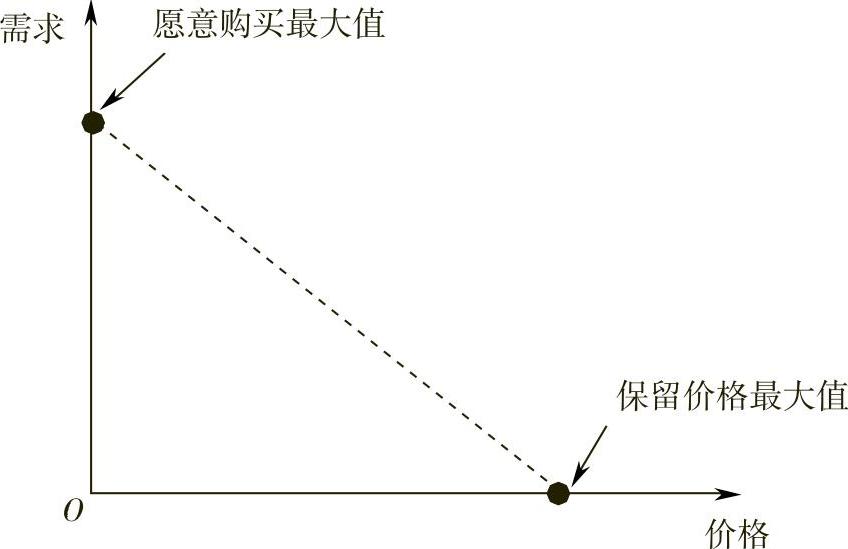
图9-1 愿意购买最大值与保留价格最大值

1）在已知愿意购买最大值（y₀）和保留价格最大值（x₀）的情况下，通过求其线性需求曲线，可以得出在一定价格下的销量水平。

方程如下：(www.xing528.com)

销量=（愿意购买最大值）×（1-价格/保留价格最大值）。

y=y₀×（1-x/x₀）

例9-1：在商善若水的慈善义卖中，某小组估计对情侣钥匙扣的需求是一个简单的价格线性方程。在价格为零时出售15对钥匙扣，当价格到达10元/对时，需求量降到零。如果价格为4元/对，则该小组可以出售多少对情侣钥匙扣呢？

解：销量=15对×（1-4元/10元）=9对

2）已知价格-销量方程中的任意两点，可以得出保留价格最大值和愿意购买最大值。

设函数上两点为（P₁，Q₁）和（P₂，Q₂），有方程如下：

愿意购买最大值=Q₁-[（Q₂-Q₁）/（P₂-P₁）]×P₁

保留价格最大值=P₁-[（P₂-P₁）/（Q₂-Q₁）]×Q₁

例9-2：在商善若水的慈善义卖中，某小组估计对情侣钥匙扣的需求是一个简单的价格线性方程。在早上的销售中发现，当价格为4元时，可以卖出9对钥匙扣，当价格为8元时，只可以卖出3对。求该价格线性方程中，愿意购买最大值和保留价格最大值分别为多少？

解：依题意，得出线性方程中的两点为（4，9）和（8，3）。

愿意购买最大值=9对-[（3对-9对）/（8元-4元）]×4元=15对

保留价格最大值=4元-[（8元-4元）/（3对-9对）]×9对=10元