现金流量与时间价值优化

（一）基本概念

现金流量是投资项目在其整个寿命期内所发生的现金流出和现金流入的全部数量，是评价投资方案经济效益的必备资料。

把某个投资看作一个独立系统，流出系统的资金称为现金流出，流入系统的资金称为现金流入，一定时期各个时间点上实际发生的资金流出或流入称为现金流量。现金流入和流出的差值称为净现金流量。

任何投资活动都需要经历一个时间段，在该时间段内，资金的流入流出、数额大小、发生的时间点都不同。为了全面、正确、直观地表现资金流动和时间的对应关系，我们借助现金流量图这个工具。现金流量图是用来反映在一定时间内资金运动状态的简化图，如图5-1所示。

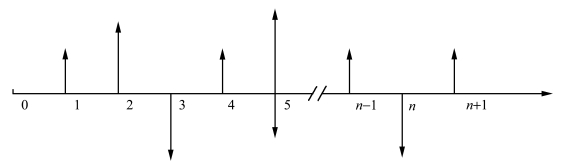
图5-1　现金流量图示意

（二）现金流量图的绘制规则

1.横轴为时间轴

轴上每一个刻度表示一个时间单位，两个刻度之间的长度称为计息周期。时间单位可以是“年”“月”“日”“季度”等。横坐标上的“0”点通常表示资金运动的时间开始点，或者是某一基准时刻，“1”“2”…“n”等数字表示第1、2、…、n个计息周期的期末，同时又是第2、3、…、n＋1个计息周期的开始。如图5-1所示。

2.期末惯例

一个计息周期内，资金的流动往往具有随机性，即并非所有资金流动都发生在周期末。为了简化计算，公认将资金流动的代数和看作在计息周期末发生。这个原则我们称之为“期末惯例”。

3.第0周期

在绘制现金流量图时，往往将初始投资看作是上一周期期末，即第0期期末。

4.箭头方向

相对于时间坐标的垂直箭头代表现金流量。向上表示正，即现金流入；向下表示负，即现金流出。

（三）资金的时间价值以及现值、终值和年金

资金的时间价值是指资金随时间发生变化，其价值在经过一段时间的投资后发生的增值。例如，现在将100元钱存入银行，1年后连本带息得到102元，那么我们可以认为现在的100元和1年后的102元是等值的；反过来，1年后的100元和现在的100元在价值上不等值。也就是说，同样数额的资金在不同的时间表现出不同的价值。再举一个例子，2009年5元钱可以买10个肉包，而2019年5元钱只能买2.5个肉包。

随着时间的推移，资金的价值会增加，从投资的角度看，资金的增值是因为时间价值的增长；从消费角度看，资金一旦用于投资，就不能用于消费，资金增值体现为放弃当前消费的损失而得到的价值上的补偿。

影响资金时间价值的因素主要有投资利润率、通货膨胀率以及风险因素。

1.现值（Present Value）

现值也称折现值，是指把未来现金流量折算为基准时点的价值，用以反映投资的内在价值。使用折现率将未来现金流量折算为现值的过程，称为“折现”。我们可以将其理解为资金在当前时间点的价值，常用P表示。

2.终值（Future Value）

终值是指一定量资金在将来某一个时间上的价值，又叫本利和，常用F表示。

3.年金（Annuity）

一定期间内每期等额收付的款项叫作年金，常用A表示。这里要注意的是等额收付这个特点。例如，某项目的投资分为3期，第一期期末投资1万元，第二期期末投资1万元，第三期期末投资1万元，那我们可以说这个投资期的年金是1万元。如果还是该项目，第一期期末投资0.5万元，第二期期末投资1万元，第三期期末投资1.5万元，那这个投资期的年金既不是0.5万元，也不是1万元，也不是1.5万元，因为每期的收付款项不等额，这时需要逐期分段计算。

（四）现值、终值和年金的关系(www.xing528.com)

现值、终值和年金之间可以通过以下6个公式进行相互转换。

1.一次整付终值公式

式中，（1＋i）n称为终值系数，记作（F／P，i，n），因此（5．1）可以写成

2.一次整付现值公式

式中，（1＋i）－n称为现值系数，记作（P／F，i，n），因此（5．3）可以写成

3.等额支付的年金终值公式

式中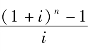，称为年金终值系数，记作（F／A，i，n），因此（5．5）可以写成

4.偿清基金公式

式中，1称为偿清基金系数，记作（A／F，i，n），因此（5．7）可以写成

5.等额支付的年金现值公式

式中，称为年金现值系数，记作（P／A，i，n），因此（5．9）可以写成

6.资金回收公式

式中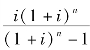，称为资金回收系数，记作（A／P，i，n），因此（5．11）可以写成

上面式子中的终值系数、现值系数、年金现值系数、年金终值系数可以通过查表获得。