基于最大熵的OWA算子权重优化算法

在绩效评价中，客观地集结客户对服务过程中服务流程要素的满意度是绩效评价的关键问题。OWA算子可通过权重的设置来集结评价者的偏好，因此，对OWA算子的优化问题成为绩效评价的关键。Yager与Filev提出了一种基于熵值的OWA算子优化^[27]，尽管这种优化算法并不能适合于所有的群决策问题，但却提出了一种新的算子优化视角。这里同样采用最大熵的原理，构建适合于产品服务绩效评价的OWA算子权重确定算法。

依据标准正态分布，Xu提出了一种OWA算子权重确定算法^[28]，即

其中ω=（ω₁，ω₂，…，ω_n）是与函数OWA相关联的加权向量，ω_i∈[0，1]，i=1，2，…，n，且有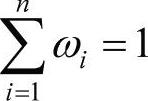，u_n为均值；σ_n（σ_n＞0）为标准差，即

这种OWA算子权重确定算法可以满足最大熵原理，但当应用于产品服务的绩效评价时，需要考虑绩效评价数据的特殊性。比如，对同一个指标，如果所有顾客评价都偏低，则认为数据真实；如果顾客评价有高有低，则认为数据存在一定的主观性。因此，当某个评价值比较极端时，应赋予较小的权值，而对于中间的数据赋予较大的权值。

定义a₁，a₂，…，a_n为评价数据集，对数据集排序，设b_j是其中第j大的数据，重新定义为(www.xing528.com)

则OWA算子权重ω=（ω₁，ω₂，…，ω_n）定义为

于是得到

评价值在结集值中被偏好的程度表达：

评价集中的数据位置表达：