最低工资标准对就业性别差异的滞后效应

1.被解释变量

在面板模型中选定合适的被解释变量非常重要，在被解释变量被确定时，选择变量的合适表达形式也会影响估计结果。根据本书研究目的，本书关心的是最低工资标准变动对就业性别差异的影响，因此被解释变量设定为就业性别差异变量。要研究最低工资标准变动对男性和女性就业的相对影响，单纯关注最低工资的变动对女性就业数量的变动或者单纯关注最低工资的变动对男性就业数量的变动，都无法达到研究目的，更无法判断最低工资的上涨是否对女性就业形成挤出效应。根据第4章的分析，本书用城镇地区女性就业比例作为性别差异变量(GD，gender difference)，该变量与男性就业比例、男女就业比例之差没有本质区别。从第4章对女性就业比例的分析来看，在较短时间内女性就业比例的变化是比较细微的，只有经过较长时间的积累，才能显著观测到就业比例的变化，对于最低工资变动对就业比例的影响，在实际观测中可能很难直观地观察到，同时最低工资上涨带来的男女就业的变化很容易被劳动人口基数增加所带来的影响所抵消。因此本书的研究基于以下假设：假设城镇地区就业的性别比例(男性比例或女性比例)在短期内是稳定的或波动范围极小，当最低工资的变动对性别比例的影响被显著观察到或波动范围达到可观测程度，则可以判断最低工资的变动对某一性别的就业者产生了挤出效应，实际研究中通常认为女性容易被挤出，可解释原因部分来自于最低工资标准变动直接或间接引起生产成本上涨进而导致劳动需求者需求行为产生变化，对就业者的劳动素质要求提高，并在面临不同性别的就业者时形成就业差别性选择。

女性就业比例数据为1996—2012年我国30个省(自治区、直辖市)城镇地区女性就业人数占全部就业人数的比例，西藏地区由于统计数据不全而且直到2004年才规定最低工资标准，因此没有被包含在样本中。由于在国家统计局公布的1998年宏观数据中缺少城镇地区女性就业人员数，因此用1998年在岗职工数代替，并用在岗职工人数中的女性比例来代替当年城镇地区女性就业比例。从历史拟合数据来看，该比例与城镇地区就业人员数的比值非常接近。

虽然我国于1993年颁布《企业最低工资规定》，但是只有北京、上海、福建、山东、海南等少数地区在1994年颁布了最低工资标准，大多数地区在1995年才颁布最低工资标准，部分地区颁布最低工资标准更迟，如甘肃在1996年才颁布最低工资标准，重庆市在1997年设直辖市后才颁布最低工资标准，为了使研究样本尽可能地多，因此在数据的时间上选择为1996年为时间起点，并将四川省1996年所公布的重庆市辖区最低工资标准设置为重庆市1996年的最低工资标准。

2.解释变量

本书关心的解释变量主要有最低工资标准AMWt及其滞后值AMWt-1(t=1996，1997，……，2012表示时间)。关于最低工资标准的确定，在当前国内外有关最低工资标准的研究文献中，使用较多的通常有三种计算方法：

(1)加权平均最低工资标准。在计算最低工资标准时，需要考虑最低工资标准在当年的实施时间范围及最低工资标准调整的时间，最低工资标准所覆盖的行业和地区，以及各个行业和地区实施最低工资标准的不同档次，结合这些因素对最低工资标准进行加权平均。如Neumark等(1992^[1]，1994^[2])、Card(1992)^[3]在计算美国联邦最低工资标准时，按照最低工资标准对行业的覆盖范围对最低工资标准进行调整，罗小兰(2007)^[4]、王梅(2010)^[5]在计算我国最低工资标准时考虑到了最低工资标准在各地区的不同档次差别；

(2)相对最低工资标准。用最低工资标准占社会平均工资或行业平均工资的比例来表示相对最低工资标准，如Neumark等(1994)在研究美国最低工资标准时曾使用过这种方法^[6]，这种设计的优势是不孤立地看待最低工资标准的影响、考虑到了最低工资标准与社会平均收入的差距，在实证时可以观测到最低工资与社会平均工资的相对影响。

(3)综合使用第一种方法和第二种方法来计算最低工资标准，即用加权平均最低工资标准与社会平均工资的比值来表示相对最低工资标准。

当然，这几种方法在实证中都是可行的，究竟使用哪种计算方法要结合研究需要和实证的目的。根据研究目的，本书采取第一种计算方法来确定最低工资标准，而不使用相对最低工资标准。从目前国内外有关最低工资的研究文献来看，最低工资标准对就业的影响本身就比较微弱，实际观测值难以准确捕捉到这种影响，而我国的最低工资相对于社会平均工资来说还明显偏低，如使用相对最低工资标准(以最低工资标准为分子、社会平均工资为分母)，将导致社会平均工资对就业的影响大大超过最低工资标准，不利于本章的静态面板模型研究。

我国各地规定最低工资标准时根据地区经济发展差异设立了不同的档次分别执行，而且在执行时间上也不一致，为方便比较各地最低工资标准，根据最低工资档次和执行时间将未作消胀处理的最低工资标准进行加权平均，得到名义加权平均最低工资，在计算加权平均月最低工资时，根据各地最低工资标准调整文件，将当年最低工资标准最高档与最低档的加权平均作为当年最低工资标准，并将实施时间引入计算中，得到调整后的当年最低工资标准，用AMWt表示，见公式(3.1)。其中t=1996，1997，……，2012表示时间，有的地区一年中经过多次调整最低工资标准，则分时间段进行加权平均。各年度月度最低工资标准AMWt见表3.3中数据。在实证研究中所有AMWt数据都利用当地的城市物价指数(城市CPI)进行消胀处理，使之成为以1990年为基期的可比较数据。

在实证中本书将最低工资标准AMWt及其滞后值AMWt-1结合起来进行研究。通常来说，当年最低工资标准的颁布时间和实施时间之间都有一个间隔期，以利于企业、个人对最低工资标准的变动有一个提前反应和过渡期，并尽量减少最低工资标准变动对就业及生产带来的冲击，因此最低工资标准对就业的很大一部分影响体现在滞后效应中。国内关于最低工资标准的研究文献中均未考虑最低工资标准的滞后值带来的影响。但是，国外有关文献中很早就已经关注到了最低工资标准的滞后效应，Charles等(1981)认为最低工资标准的滞后影响一方面来自于雇佣和培训成本变动因素以及无法快速调整其他要素的投入量，另一方面来自于最低工资标准的颁布往往超前于其真正产生效应^[7]。Card(1992)认为最低工资的滞后效应来自于最低工资标准的颁布与劳动雇佣者真正调整工资之间存在着一个明显的时间滞后^[8]。Neumark等(1992，1994)在重新检验美国1973—1989年间最低工资标准的变动对就业的影响时，观察到了最低工资标准变动对就业影响的滞后效应，经验分析和理论分析的结果表明，在回归方程中如果缺省最低工资标准的滞后值，所得到的结果会比实际结果偏大，即忽略最低工资的滞后值会引起回归结果向上偏斜^[9]。借鉴国外的研究成果，本书在静态面板模型中增加最低工资标准的滞后值，以考察我国最低工资标准对就业影响的滞后效应。由于我国《最低工资规定》要求最低工资标准至少应在每两年内作一次调整，在最低工资制度实行早期绝大部分地区的最低工资标准一般两年调整一次，少部分经济发达地区，如北京、上海、福建，最低工资标准调整相对频繁，一般每年作一次调整，但近年来，大部分地区一般每年调整一次。因此本书在设定最低工资标准的滞后期数时考虑到了我国最低工资标准实施的实际情况，将滞后期数设定为一年，因为如果最低工资的滞后期数超过一年，实际观测值中将包含最低工资的滞后效应与新的最低工资变动效应的叠加，因此无法单独识别滞后效应。

3.控制变量

在实证分析中本书还将其他一些重要的影响变量进行控制，这些变量在经济实际运行中有可能对被解释变量——就业性别差异——产生作用，将这些影响变量的影响从就业性别差异的总影响中进行分离后，就可以分析最低工资标准变动对就业性别差异的影响：

(1)教育经费投入变量。该变量用各地教育经费投入占当年经济总量(GDP)的比例来表达，该变量在实证中的作用是用来衡量教育经费的相对投入对就业性别差异的影响。国家统计局公布的各地年度教育经费只有地方教育经费数据，而不含中央财政经费的分解数据，但中央财政经费该数据在教育经费总额中占比并不大(2009年约为11%)，因此本书在计算教育经费占GDP的比重时没考虑中央财政预算额。1996年的重庆教育经费欠缺，根据四川和重庆的经费总额的年度增长率作估算得到。

(2)人口因素。该变量用各地经济活动人口(即15～64岁劳动人口)在总人口中的比例来表达，该变量在实证中的作用是用来考察人口因素对就业性别差异的影响。2000年和2010年数据为当年人口普查数据，和其他年份数据统计口径不一致，本书根据历史数据作了修正。

(3)经济发展因素。该变量用人均GDP变量来衡量各地经济发展水平对就业性别差异的影响。(www.xing528.com)

(4)地区差异。涉及到中西部差异、城市化程度的差异，实证中引入两个虚拟变量：东部与中部、西部地区虚拟变量，直辖市与非直辖市虚拟变量。

(5)《最低工资规定》实施时间的影响。主要考察《最低工资规定》在2004年实行是否对2004年前后的就业性别差异产生显著影响，实证中引入虚拟变量：2004年之前与2004年之后。

在静态面板模型中共控制了3个实际变量和3个虚拟变量。各变量所使用的数据分别来源于1996—2013年度的《中国统计年鉴》、《中国劳动统计年鉴》、《中国人口统计年鉴》，部分数据还参考了地方统计年鉴(如1996年重庆数据来源于《重庆统计年鉴》)，人均GDP变量平减为以1990为基期。表6.1描述了相关变量的定义，表6.2给出了各实际变量的统计描述。

表6.1　实证分析中的变量定义及统计描述

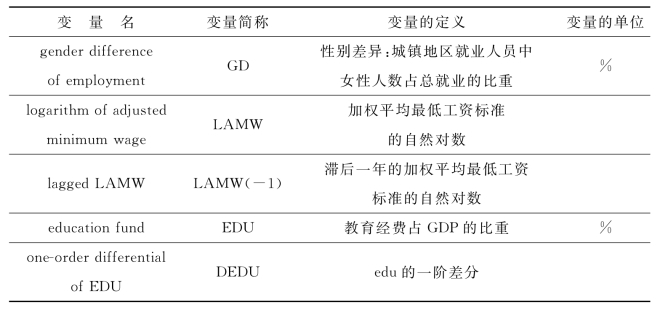
续表

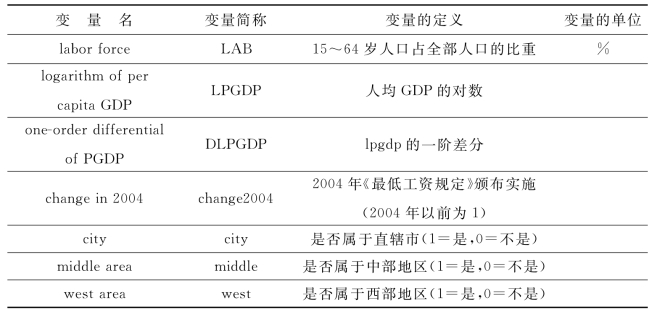
　　注：(1)由于1998年国家统计局未公布城镇单位女性就业人员数，本书用当年在岗职工人数中女性人数的占比代替，从历史数据来看，该比值与城镇单位就业人员数的比值实际差距较小。(2)国家统计局公布的各地年度教育经费只有地方教育经费数据，而不含中央财政经费的分解数据，但中央财政经费该数据在教育经费总额中占比并不大(2009年约为11%)，因此本章在计算教育经费占GDP的比重时没考虑中央财政预算额。1996年的重庆教育经费欠缺，根据四川和重庆的经费总额的年度增长率作估算得到。(3)2000年和2010年数据为当年人口普查数据，和其他年份数据统计口径不一致且相比显得异常，因此对实证效果可能有些影响。

表6.2　实证分析中实际变量的统计描述

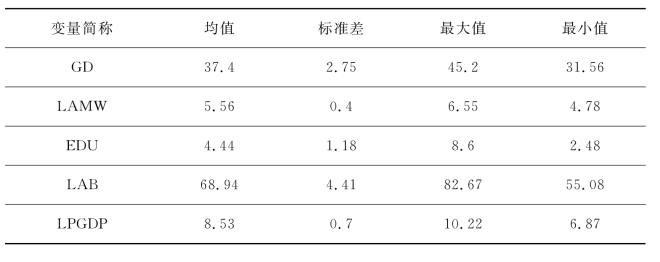
4.变量的平稳性检验

为了防止面板数据模型回归中出现虚假回归或者伪回归，需要对变量进行平稳性检验，如果变量为非平稳的，则进入模型的变量形式需作相应的变换。各实际变量的平稳性检验结果见表6.3。

表6.3　变量平稳性检验结果

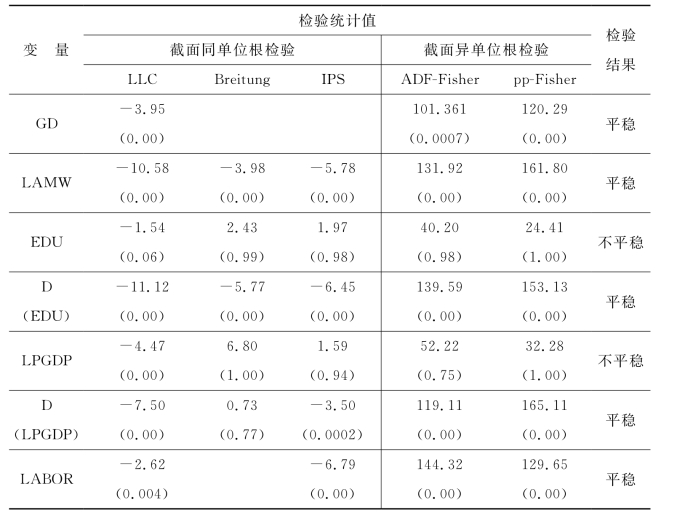
　　注：表中括号中的数字为伴随概率。

表6.3中检验结果显示，GD、LAMW、LABOR为平稳变量，EDU、LPGDP为一阶单整变量。