就业性别差异的密度分布情况

核估计是密度函数估计的一种非参数估计方法。这种方法的实质是通过已知观测值X1，X2，……，Xn来估计一般选择值的概率分布。对这种方法，本书可以从均匀分布出发加以简要阐述。

假设x为服从均匀分布的随机变量，X1，X2，……，Xn为它的一个独立同分布的样本，设x的分布函数为

则其密度函数估计为

将核函数K0推广到一般核函数K时，就得到了密度核估计的一般公式

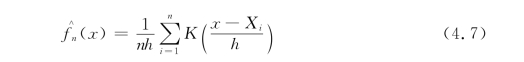
其中，h被定义为窗宽，h的选择要求满足条件：当n→+∞时，h→0，nh→+∞。窗宽h的确定常用交错鉴定方法、惩罚函数法和插入法等。常用的核函数有均匀核函数、高斯核函数、三角核函数、Epanechnikov核函数等。本研究选取Epanechnikov核函数来估计核密度，其表达式为：(www.xing528.com)

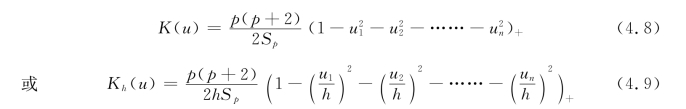
其中

ui=x-Xi，　S=2πp/2/Γ(p/2)

　　Γ为伽马函数，h为窗宽，p为随机变量的维度。实际计算时采用Stata软件进行自动估计和窗宽选择，得到p=1，h=0.0275。

从1996年开始，每隔5年选取一个典型年份，作出1996、2001、2006、2011年的核密度估计曲线，以考察城镇地区就业性别差异分布的演化状况。在每年中，以30个地区10个行业的就业性别差异作为个体，共计300个样本，其核密度估计曲线如图4.4所示。

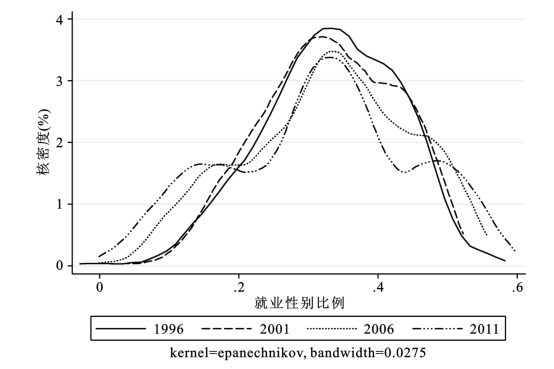
图4.4　典型年份就业性别比例核密度图

从图4.4中可见，女性就业比例出现了很清晰的三段分布，临界值点大致为0.2和0.5：就业比例小于0.2的部分，密度分布逐年向左偏移；就业比例大于0.5的部分，密度分布逐年向右偏移；而就业比例在0.2～0.5的部分，密度分布逐年向内收敛，密度峰值逐年下降。结合表4.1，10个行业的女性就业比例各年度均值在0.3～0.35之间，就业性别比例低于0.2或大于0.5的所占比重较小，也即就业性别比例在0.2～0.5之间的分布可以反映各年度的主要分布状况。在此基础上对分布状况进行分析可以发现，相对1996年来说，2001年、2006年、2011年分布逐年发散，在绝大部分行业，女性的就业比例趋于下降，表明就业的性别差异在扩大，而在女性就业比例较低(低于20%)和较高(高于50%)的行业，女性就业比例在逐年上升。一个可能的猜想是：在某些特别适合女性工作的行业，女性劳动者加速流入；而在某些不适合女性工作的行业，女性劳动者也愿意参与就业；而在女性和男性就业无差异的行业，女性正被逐年挤出。