归因分析的方法及应用

前面我们介绍了加法形式分解分析的一般模型，根据公式（7.7），驱动因素i对指标V的Laspeyres型和Divisia型加法形式效应可以分别表示为：

其中，和表示子类（如行业部门）j对驱动因素i效应的贡献。

在乘法形式分解分析模型中，乔伊和安（Choi and Ang，2012）采用莱因斯多夫等（Reinsdorf et al.，2002）和鲍克（Balk，2004）的几何平均指数和算术平均指数转换方法，提出了将驱动因素乘法形式效应表示为各子类相应因素贡献之和的方法，这种方法称为归因分析（Attribution Analysis）。以LMDI-II乘法形式分解分析为例，根据公式（7.14），在［0，T］时期内，驱动因素i对指标V的效应可以表示为：

令未知变量πj满足如下等式：

我们进一步定义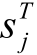和如下：

根据鲍克（Balk，2004），公式（7.30）满足以下等式关系：

其中，

将公式（7.36）带入公式（7.35），并对求解，可以得到：

比较公式（7.32）和（7.36），可知未知量πj满足如下等式：(www.xing528.com)

由公式（7.33）和的定义可知：

从而，

其中，

根据公式（7.36），驱动因素i使指标V变动的百分比为，其中来自子类（如行业部门）j的贡献为。

当我们拥有T+1期（0＜1＜2＜…＜(T-1)＜T ）数据时，驱动因素i在［0，T］时期内对指标V的乘法形式影响Gi(0,T)满足以下等式：

其中，Gi(t-1,t)表示驱动因素i在［t - 1，t］时期对指标V的影响。由公式（7.40）和（7.42）可知，多时期归因分析可通过以下等式展开：

其中，

是基于0时期衡量的［t - 1，t］时期驱动因素i对指标v的效应中来自子类j的贡献百分比。