分解分析方法的框架及应用领域

根据苏和安（Su and Ang，2012b）以及王等（Wang et al.，2017）的论述，分解分析所处理的整体指标V可以一般性地表示为

其中，vj是该指标子类j的数值，xji表示该指标子类j的第i种驱动因素的值，m和n分别是该指标子类的数量和驱动因素的数量。在实证研究中，子类一般指产品或产业部门。假设我们拥有0和T时期两组数据，则指标V在［0，T］时期内算术变化和期末期初比率可以分别表示为

其中，ΔiV和iG分别是驱动因素i的加法形式效应和乘法形式效应；ΔiV大于零或iG大于1时表示驱动因素i推动了指标V的增长，ΔiV小于零或iG小于1时则表示驱动因素i导致了指标V的下降；ΔVrsd和Grsd分别是加法形式分解和乘法形式分解的残余项，在完全分解中，两项分别为0和1。

对指标V做微分，有

指标V在［0，T］时期内算术变化ΔV可以表示为

将公式（7.4）带入公式（7.5）得到

其中，公式（7.6）的第一行右式是Laspeyres型加法分解式，公式（7.6）的第二行右式是Divisia型加法分解式，两者的差异来源于积分路径的选择，前者使用驱动因素的线性变化，后者使用驱动因素的对数变化。假设公式（7.6）中的被积函数

在［0，T］时期内保持不变，则ΔV可以近似地表示为

其中，

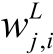和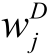分别表示Laspeyres型和Divisia型加法分解式的权重函数（Weight Function），和ΔV(t-1,t)分别表示Laspeyres型和Divisia型加法分解式中驱动因素i的效应。

根据苏和安（Su and Ang，2012b）的论述，加法形式D&L方法属于Laspeyres型分解方法，其权重函数为

其中，

加法形式LMDI-I和LMDI-II方法属于Divisia型分解方法，其权重函数分别为

其中，(www.xing528.com)

其他加法形式分解方法的权重函数参见王等（Wang et al.，2017）的论述。

对lnV做微分，有

指标V在［0，T］时期内的对数变化ΔlnV可以表示为：

将公式（7.11）带入公式（7.12），有：

类似的，公式（7.13）第二行右式是Laspeyres型乘法分解式，公式（7.13）第三行右式是Divisia型乘法分解式。假设公式（7.13）中的被积函数

在［0，T］时期内保持不变，则VT /V0可以近似地表示为：

其中，

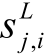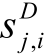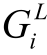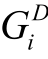和分别表示Laspeyres型和Divisia型乘法分解式的权重函数， 和分别表示Laspeyres型和Divisia型乘法分解式中驱动因素i的效应。

根据王等（Wang et al.，2017）的论述，乘法形式D&L方法的权重函数为：

其中，

乘法形式LMDI-I和LMDI-II方法的权重函数分别为：

其他乘法形式分解方法的权重函数参见王等（Wang et al.，2017）的论述。

最后，需要指出的是，在分解分析应用中，需要对不同时期的数据进行价格处理，以剔除价格波动对分解结果的影响。