股权激励下管理层股利分配方式偏好模型

为克服样本选择问题，本书沿用第三章的分析框架，用倾向得分匹配法(PSM)，选用公司特征变量为实施股权激励公司匹配出非股权激励上市公司。匹配过程和匹配后的检验参照第三章。在PSM模型框架下，建立多项Logit模型考察股权激励下管理层股利分配方式偏好。

(一)多项Logit模型初探

本书在倾向得分匹配模型基础上，建立多项Logit模型探讨:与非股权激励上市公司相比，股权激励公司管理层对股利分配方式的偏好程度有何区别。Logit模型的被解释变量为股利分配方式。本书首先将上市公司股利分配方式分为:不发放任何形式的股利、仅发放现金股利、仅发放股票股利、混合股利(同时发放现金股利和股票股利)，即上市公司面临多个没有顺序关系的选择。可供上市公司选择的股利分配方式有四项，这四项相互排斥。使用随机效用法，假设上市公司i选择股利分配方式j所能带来的随机效用为:

其中xi只随个体i而变化，不随方案j而变化。系数βj表示，xi对随机效用Uij的作用取决于方案j。显然，当且仅当股利分配方式j带来的效用高于所有其他方案时，上市公司i才会选择方案j，此时上市公司i选择方案j的概率可表达为:

4.9式可进一步表述为4.10式和4.11式。

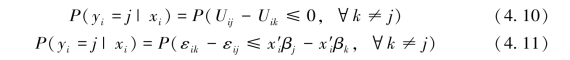
其中，{εij}为iid且服从I型极值分布，此时上市公司i选择股利分配方式j的概率可进一步表达为:

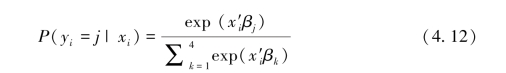
显然，选择各项股利分配方式的概率和为1，即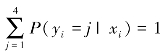。因为无法同时识别所有的系数βj，所以需要将某项股利分配方式作为“参照方式”，令其相应的系数为0。如果将不分配、仅发放现金股利、仅发放股票股利、混合股利四种方式分别定义为1，2，3，4，当将不分配定为“参照方式” 时，其相应系数β1＝0，此时，上市公司i选择其他方式的概率为:

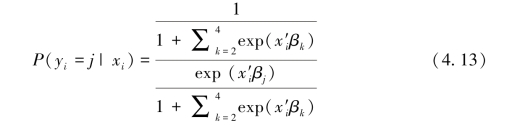
该多项Logit可用MLE进行估计。上市公司i的似然函数为:

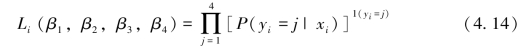(www.xing528.com)

其对数似然函数为:，

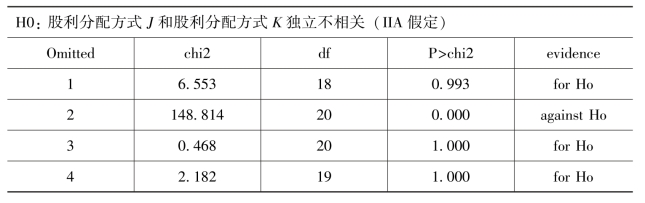
其中L(.)为示性函数。对该模型的使用，需检验股利分配方式是否满足“无关选择的独立性”。本书首先用豪斯曼检验对最初定义的四个股利分配方式进行检验，结果如表4-2所示。

表4-2　“无关选择的独立性”豪斯曼检验1

(二)多项Logit模型的修正

豪斯曼检验结果提示对被解释变量股利分配方式分成四类违背了IIA假定，于是，本书对股利分配方式重新分成不发放任何形式的股利、仅发放现金股利、发放股票股利三类，并分别定义为方式1、方式2和方式3。显然在这种分类方式下，各方式之间依然互相排斥，其豪斯曼检验结果如表4-3，该表表示去掉两个非参照方式中的任何一个方式，都不会拒绝IIA的原假设。所以，本章将股利分配方式最终确定为不发放任何形式的股利、仅发放现金股利和发放股票股利三类，分别定义为方式1、方式2和方式3，其中方式3包含了最初定义的仅发放股票股利和混合股利，股利分配方式用变量PayChoice来表示。

表4-3　“无关选择的独立性”豪斯曼检验2

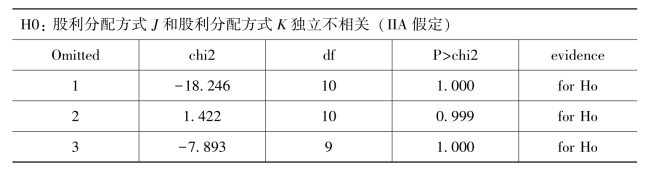
在以上检验步骤下，本章最终确定上市公司i的股利分配方式为3个，于是上市公司i选择方式j的概率可修正为:

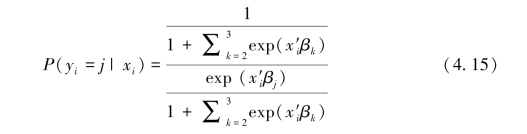
在此基础上，根据本书提出的研究假设，本书建议以下多项Logit模型:

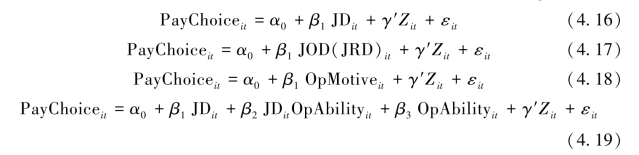
式(4.16)检验股权激励管理层是否在股利分配方式上存在机会主义行为，式(4.17)检验两种不同的激励工具对股利分配方式偏好的差异性影响，式(4.18)检验考察管理层机会主义动机对股利分配方式偏好的影响，式(4.19)考察管理层机会主义行为实现能力对股利分配方式偏好的影响。PayChoice为股利分配方式，JD、JOD、JRD分别为股权激励计划哑变量、股票期权哑变量、限制性股票哑变量，OpMotive为股权激励管理层机会主义动机变量，OpAbility为股权激励管理层机会主义实现能力变量。Zit为影响股利分配方式的控制变量，εit为模型的随机扰动项。