企业利润受何影响？

结论7　零售商受益于以旧换新消费比例的增大。

证明　由于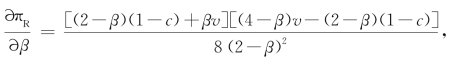而（4-β）v＞（4-2β）v=（2-β）2v＞（2-β）（1-c）（由推论1可知，2v＞1-c）。因此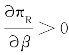，，即零售商的利润随着以旧换新消费比例的增大而逐渐增大（可以从图2-4中看出零售商利润随着以旧换新比例增加而发生的变化）。因此，零售商受益于以旧换新消费比例的增大。

结论8　随着以旧换新消费比例的增大，回收商的利润从无到有，并逐渐增大至极值后有所下降。

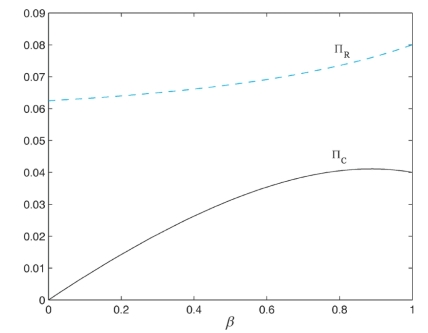
图2-4　消费者结构对企业利润的影响（c=0.5和v=0.3）

证明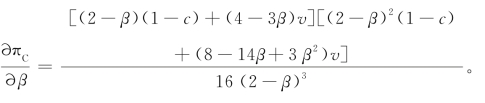　

令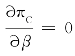，即[（1-c）+3v]β2-2[2（1-c）+7v]β+[4（1-c）+8v]=0。经分析，该等式有两个实根：(www.xing528.com)

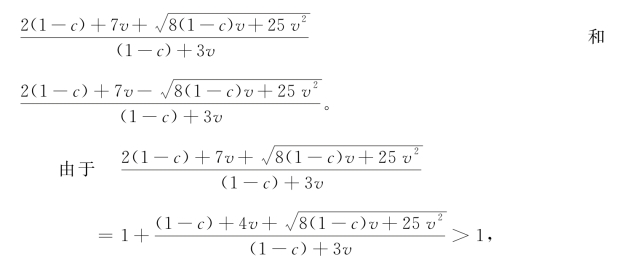
该根不在有效的范围内（β∈[0，1]），那么另一个根在有效的范围内吗？还是回收商的利润随着以旧换新比例的增加而单调递增或递减？由于[2（1-c）+7v]2=4（1-c）2+28（1-c）v+49 v2＞8（1-c）v+25 v2，因此，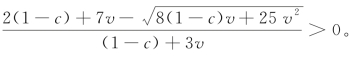

接下来还需要判定该根是否小于1。

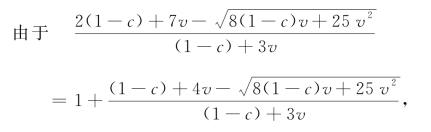
当且仅当时，此根在有效范围内。

由于[（1-c）+4v]2=（1-c）2+8（1-c）v+16v2，只需比较（1-c）2和9v2的大小关系即可。由推论1可知2v＞1-c，而3v=2v，因此，3v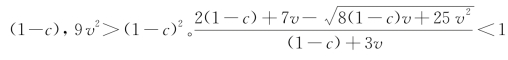＞，此根在有效范围内。

综上所述，在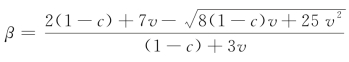时，回收商的利润达到一个极值。经简单分析（β=0时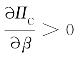，）可知，该极值为极大值。因此，随着以旧换新消费比例的增大，回收商的利润从无到有，并逐渐增大至极值后有所下降（从图2-4中看出，回收商利润随着以旧换新比例增加而发生的变化）。