优越性能的ECC算法：解决椭圆曲线离散对数问题

1.ECC密码体制简介

ECC是基于椭圆曲线离散对数问题的各种公钥密码体制。最早是在1985年分别由V.S.Miller和Neal Koblitz独立提出的。从1985年以来，ECC受到了全世界密码学家、数学家和计算机科学家的密切关注。一方面，由于没有发现ECC明显的安全漏洞；另一方面，在提高ECC的实现效率上取得了长足的进步，现在ECC已成为效率最高的公钥密码体制。

相对于RSA和DSA（一种数字签名算法，见2.4.1节）等系统，ECC最吸引人的原因是目前已知的解决椭圆曲线离散对数问题（ECDLP）最好的算法，也是完全指数时间的。与之相比，RSA和DSA等其他公钥密码系统所基于的数学问题，如因数分解问题（IFP）和离散对数问题（DLP）都有亚指数时间算法。与RSA和DSA等体制相比，ECC具有如下优势。

（1）安全性更高

加密算法的安全性能通过算法的抗攻击强度来反映。表2-8描述了ECC和其他几种公钥密码算法抗攻击强度的比较。可以看到，与其他公钥算法相比，ECC抗攻击性具有一定的优势。如160bit的ECC可提供与1024bit的RSA/DSA相当的安全强度，而210bit的ECC则与2048bit的RSA/DSA具有相同的安全强度。

表2-8 ECC与RSA/DSA抗攻击性能比较

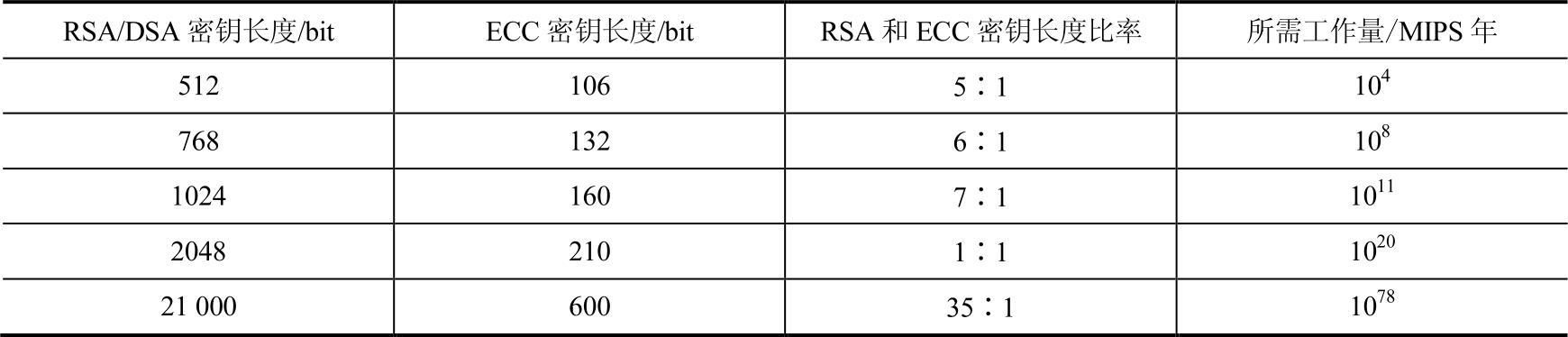
注：其中“MIPS”年表示每秒钟运行一百万次指令的计算机运行一年的工作量。

（2）计算量小，处理速度快

虽然在RSA中可以通过选取较小的公钥（如选取3为公钥）的方法提高公钥处理的速度，即提高加密和签名验证的速度，使其在加密和签名验证上与ECC有可比性，但在私钥的处理速度上（解密和签名），ECC比RSA/DSA要快。而且随着安全强度的增加，ECC比RSA/DSA运算的速度提高得更快。

（3）需要的存储空间少

ECC的密钥尺寸和系统参数与RSA/DSA相比要小得多，意味着它所占的存储空间要少得多。这对于在IC卡和无线环境中的应用具有特别重要的意义。

（4）带宽要求低

当对长消息进行加解密时，3类密码体制有相同的带宽要求，但应用于短消息时，ECC对带宽要求要低得多。带宽要求低使ECC在无线网络中具有广阔的应用前景。

由上面的几点可以看出，随着计算能力的提高、需要密钥长度的增加，ECC相对其他公钥密码系统具备一定的优势。其每比特更高的安全性所带来的优点包括：更高的速度、更低的能量消耗、节约带宽和提高存储效率。这些优点在一些对于带宽、处理器能力或存储有限制的应用中显得尤为重要。

2.ECC密码体制的数学基础

随着ECC研究的不断深入，ECC的标准化工作也在紧锣密鼓地进行中。ECC已被纳入IEEE公钥密码标准P1363中，包括加密、签名、密钥交换机制等。同时，ANSI也在制定椭圆曲线的相关标准，其中包括椭圆曲线数字签名算法（ECDSA）标准ANSI X9.62与椭圆曲线密钥协商和传输协议标准ANSI X9.63等。此外，ISO和ATM等组织也在对椭圆曲线的应用制定相关标准。

（1）Weierstrass方程

在代数几何中，亏格为1的代数曲线称为椭圆曲线。由Riemman-Roch定理可知，任何一条椭圆曲线总可以用一个三次方程来表示，这个三次方程一般称为Weierstrass方程。下面给出椭圆曲线的定义。

设一给定的域K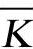，为它的代数闭域，定义在域K上的Weierstrass方程

E：Y²Z+a₁XYZ+a₃YZ²=X³+a₂X²Z+a₄XZ²+a₆Z³

称为射影平面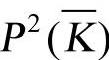上的椭圆曲线。

其中，a₁，a₃，a₂，a₄，a₆∈K。

设F（X，Y，Z）=Y²Z+a₁XYZ+a₃YZ²−（X³+a₂X²Z+a₄XZ²+a₆Z³）

当方程组

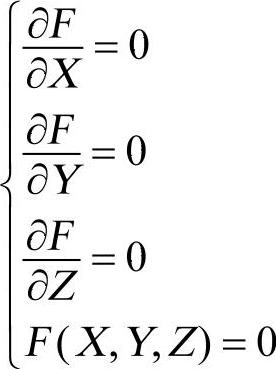
在K上无解，则称该曲线E是非奇异（Non-singular）的，否则称E为奇异的（Singular）。

Weierstrass方程在射影平面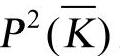上的解的集合为

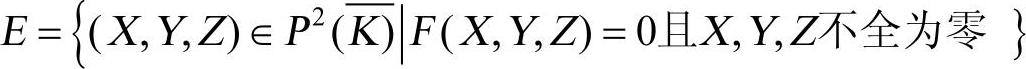
对于椭圆曲线，坐标分量Z=0的唯一的有理点（0，1，0），称为无穷远点，记为O。

对Weierstrass方程，现令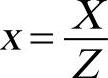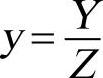，，则方程可变为

y²+a₁xy+a₃y=x³+a₂x²+a₄x+a₆

（2）有限域上的椭圆曲线及其运算规则

根据有限域K的特征Char（K）的不同，通常分为Char（K）=2、Char（K）=3和Char（K）≠2，3三种情况。考虑到在ECC中，通常选择Char（K）=2和Char（K）=p（p为大素数）。下面只介绍Char（K）≠2，3和Char（K）=2两种情况。

1）Char（K）≠2，3时的情况

如果在有限域K上定义的椭圆曲线的特征值不等于2和3，那么椭圆曲线的Weierstrass方程可以大大简化。可以得到有限域K上的椭圆曲线为

E：y²=x³+ax+b （a，b）∈K

其判别式∆及j不变量分别为∆=-16（4a³+27b²）和j（E）=-1728（4a）³/∆，由于E是非奇异的，因而∆≠0。

此时的加法规则如下。

若P=（x₁，y₁）∈E，则-P=（x₁，−y₁）。若Q=（x₂，y₂）∈E且Q≠−P，则P+Q=（x₃，y₃）。其中：x₃=λ²−x₁−x₂，y₃=λ（x₁−x₃）−y₁。且当P≠Q时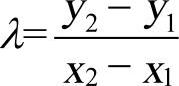，；当P=Q时，。

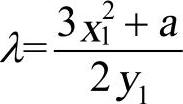令E为有限域K上的形为y²=x³+ax+b的椭圆曲线，设P和Q为E上的两个点，-P和P+Q的定义如下：(www.xing528.com)

●若P是椭圆曲线E上的无穷远点O，则-P为O，且P+Q=Q，这里的P可以看成是加法幺元。

●若P=（x，y），则-P=（x，-y）。

●若P和Q的x坐标不同，则直线L=PQ截椭圆曲线有且仅有一点R（若L为椭圆曲线的切线，则令切点R=P或R=Q），定义P+Q=R。其示例分别如图2-18和图2-19所示。

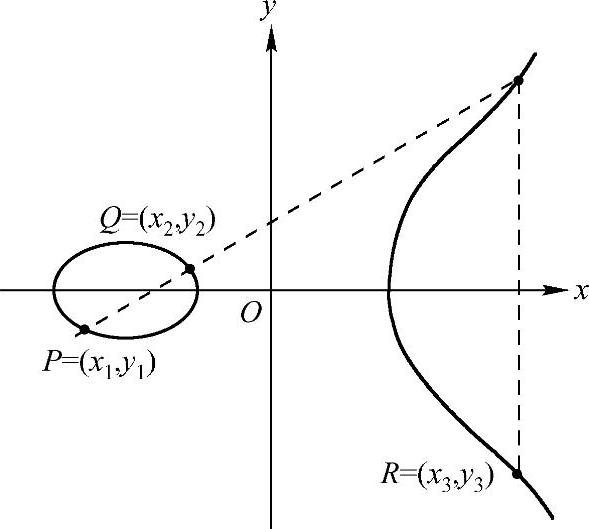
图2-18 椭圆曲线上的加法P+Q=R

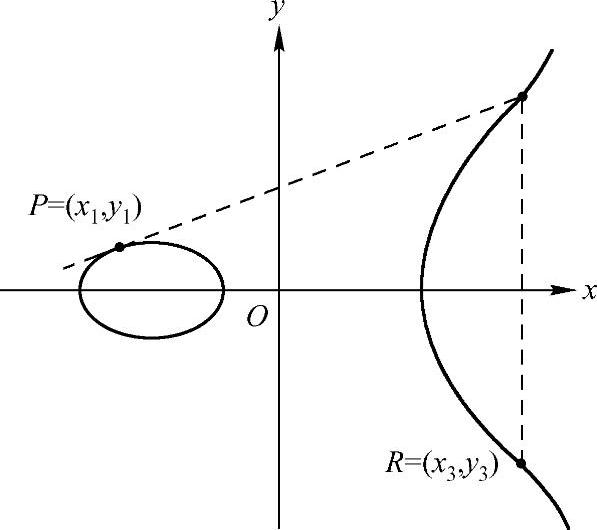
图2-19 椭圆曲线上的加法P+P=2P=R

●若P≠Q，且P和Q的x坐标相同（y坐标必定相反），则P+Q=O。

●若P=Q，令L为椭圆曲线上P点的切线，L截椭圆曲线仅有一点R，则P+Q=2P=R，由此可以计算2P。

●P+Q称作点加，k个相同点相加，即P+P+…+P表示为kP，则称为点乘或数乘。

2）Char（K）=2时的情况

设K为一有限域，其特征值等于2，令E/K为由Weierstrass方程定义的椭圆曲线

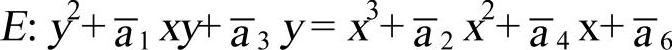
则其j不变量为

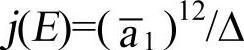
如果j（E）≠0（因而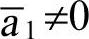），那么可以将E转换为椭圆曲线E1

E₁/K：y²+xy=x³+a₂x²+a₆

对于E₁有

∆=a₆及j（E₁）=1/a6

如果j（E）=0（因而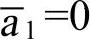），那么可以将E转换为椭圆曲线E2

E₂/K：y²+a₃y=x³+a₄x+a₆

对于E₂有

∆=a⁴₃及j（E₂）=0

此时的加法规则如下。

●当j（E）≠0时，令P=（x₁，y₁）∈E₁，则−P=（x₁，y₁+x₁）。若Q=（x₂，y₂）∈E₁且Q≠−P，那么P+Q=（x₃，y₃）。其中

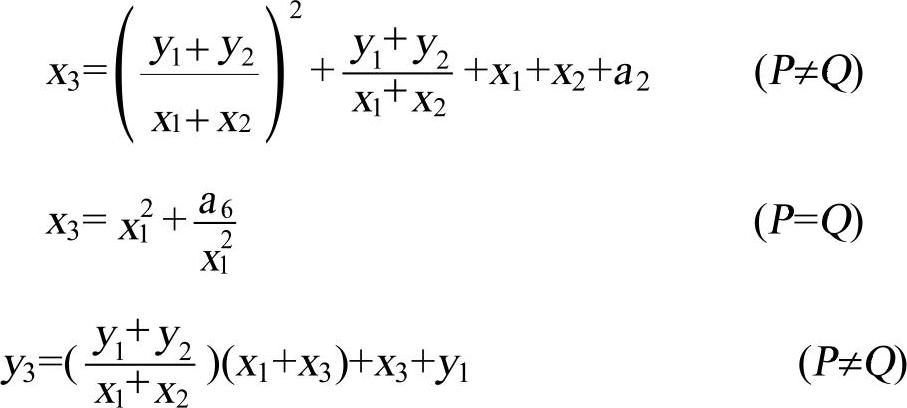
●当j（E）=0时，令P=（x₁，y₁）∈E₂，则-P=（x₁，y₁+a₃）。如果Q=（x₂，y₂）∈E₂，并且Q=-P，那么P+Q=（x₃，y₃）。其中

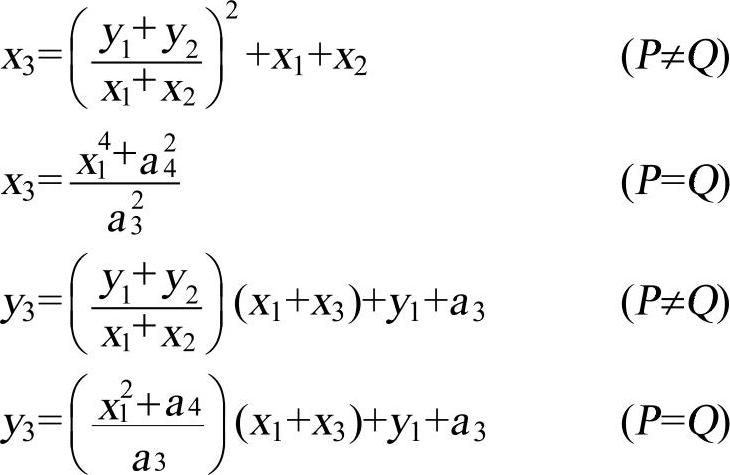
3.ECC的应用

在椭圆曲线上可以方便地实现ElGamal密码体制。设Alice要向Bob发送信息m，首先，Alice把明文m嵌入到E上的点P_m；然后，Alice随机选择一整数k，计算kP和P_m+kP_b，并将（kP，P_m+kP_b）发送给Bob。

Bob收到信息后，计算P_m=（P_m+kP_b）-d_b（kP），并从P_m中恢复出明文m。

下面介绍一个把m嵌入到E上的点P_m的一种方法。设q≡3（mod 4），m是一个整数，且0≤m＜q/1000-1。向m后面添加3位十进制数将构成一个新数x，有1000m≤x<1000（m+1）＜q。通过不断尝试这一过程直到找到一个x使得f（x）=x³+ax²+b为mod q的平方剩余。这样，定义m嵌入的点为_Pm=（x，f（x）^（q+1）/4）

恢复明文m很简单，只要把解密后的P_m的x坐标去掉后3位即可。

除了可以把明文m嵌入到E上外，也可以通过Masking方法来处理明文m。Menezes-Vanstone椭圆曲线密码系统就采用这种方法：

设Alice要发送m=（x₁，x₂）∈Zq^*×Zq^*。首先，Alice随机选择一整数k，计算y₀=kP，（c₁，c₂）=kP_b，y1=c₁x₁modq，y₂=c₂x₂modq，并将（y₀，y₁，y₂）发送给Bob。Bob收到信息后，计算（c₁，c₂）=d_by₀，并从（y₁c₁^-1modq，y₂c₂^-1modq）=（x₁，x₂）中恢复出明文m。

用椭圆曲线也可以很容易实现Diffie-Hellman密钥交换。

设Alice和Bob分别选取随机数a和b予以保密，将aG，bG∈E公开。则Alice和Bob间通信用的密钥为abG，这是第三方无法得知的。

Diffie-Hellman密钥交换协议可以很容易地扩展到3人或更多的人。但是，Diffie-Hellman密钥交换协议不含有交换双方的认证信息，不能抵抗中间人攻击。