RSA算法简介：公钥密码体制的经典代表

1977年，Ron Rivest、Adi Shamir和Leonard Adleman提出了公钥密码算法RSA。它既能用于加密，又能用于数字签名，易于理解和实现，是第一个较为完善的公钥密码体制。RSA的安全性基于大整数分解的困难性。

1.RSA密码体制描述

选取两个不同的大素数p和q，为了获得最大程度的安全性，p和q的长度一样。计算它们的乘积

n=pq

令ϕ（n）=（p−1）（q−1）。

随机选取一个整数e，1≤e≤ϕ（n），（ϕ（n），e）=1。因为（ϕ（n），e）=1，所以在模ϕ（n）下，e有逆元d=e⁻¹modϕ（n）。

e和n为公钥，d是私钥。两个素数p和q不再需要，可以销毁，但绝不能泄露。

（1）加密

加密消息m时，首先将它分成比n小的数据分组。对于其中任一个分组x，加密公式为

y=x^emod n

（2）解密

解密消息时，对于任一个密文块y，计算

x=y^dmod n

因为

y^dmod n=（x^e）^dmod n=x^edmod n=x^kϕ（n）+1mod n=x(www.xing528.com)

所以该公式能恢复明文x。

加密和解密运算都是模n指数运算。因为n很大，所以必须使用一些有效算法来完成Z_n中的计算，而且需要的计算时间将是依赖于n的二元表示的位数，即n的长度。假定n的长度为k，则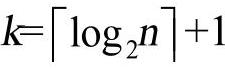，使用标准的算术技术。不难看出，两个k bit的整数的加法能在时间O（k）内完成，乘法能在O（k²）内完成。一个长度至多为2k的整数的模n运算能在时间O（k²）内完成。假定x，y∈Zn，那么xy mod n可以按照下述方法计算：先计算积xy（xy是一个长度为2k的整数），然后对xy进行模n归约。这两步可以在时间O（k²）内完成，该计算称为模乘法。x^cmod n的计算可以使用c−1次模乘法完成。然而，如果c很大的话，这种做法就不是很有效了。“反复平方—乘”算法是计算模指数的一种有效算法。这种算法计算x^cmod n至多需要2l次模乘法，这里的l是c的长度。因为l≤k，所以x^cmod n能在时间O（k³）内完成。

2.RSA密码体制的安全性分析

密码分析者对RSA密码体制的一个明显的攻击是分解n。如果能做到这一点，那么很容易就能计算出ϕ（n），然后通过计算d=e⁻¹modϕ（n）来获得私钥d。因此，如果RSA密码体制是安全的，那么n=pq必须足够大，使得分解它在计算上是不可行的。目前的分解算法能分解的整数已经达到130位的十进制数。因此，基于安全性考虑，用户选择的素数p和q应当大约都为100位的十进制数，那么n=pq将是200位的十进制数。RSA的一些硬件实现使用一个512bit长的模，然而一个512bit长的模相当于大约154位的十进制数，所以从长远的角度来看，512bit模不能提供足够高的安全性。

n已知时计算ϕ（n）与分解n的问题是等价的，而且当p和q未知时没有有效算法可以计算出群Z^*_n中元素的e次方根。因此，人们猜测破译RSA密码体制多项式等价于分解n，但是这一点仍未被证明。因此，RSA密码体制的安全性是建立在整数分解问题之上的。整数分解方面的算法研究已经取得了很大的进展，两种可行的算法是椭圆曲线算法和多项式平方筛选算法。以目前的知识和技术，如果p和q是100位的十进制数，分解n为不可能的。

如果密码分析者能够计算ϕ（n），那么他一定能分解n，从而破译该体制。这是由于可以通过下列方程组获得因子p和q：

n=pq

ϕ（n）=（p−1）（q−1）

这个方程组可以转化为方程：p²−（n−ϕ（n）+1）p+n=0

这个方程的两个根便是p和q，即n的因子。也就是说，计算ϕ（n）并不比分解n容易。事实上如果知道ϕ（n）并不需要去分解n，只要用Euclid算法就可以从加密密钥e计算出解密密钥：

d=e⁻¹modϕ（n）

求解私钥d和分解大整数n是等价的。也就是说，给定私钥d，可以分解n；反过来，给定n的分解形式，可以恢复私钥d。

近年来，RSA密码体制受到了严重威胁。1999年8月27日，阿姆斯特丹国立数学和计算机科学研究所的研究人员用一台克雷900-16超级计算机、300台个人计算机以及专门设计的软件用6个星期破译了RSA-155密码。