高级加密标准AES解析

1997年6月18日，美国科罗拉多州以Rocke Verser为首的一个工作组宣称破译了DES加密算法。解密的明文为Strong cryptography makes the world a safer place，解密密钥为8558891AB0C851B6，RSA数据安全公司已证实它的正确性。加密消息的密钥量约为7.2×10¹⁶，工作组以7.0×10¹⁰/s的速度测试了其中的1/4，即1.8×10¹⁶。搜索到正确的密钥，前后历时4个多月。破译成功无疑宣布了DES（数据加密标准）的不安全性，使美国政府重新审视其现行的加密标准。

AES（Advanced Encryption Standard）是NIST筹划的，旨在取代DES，是一种保护政府敏感信息的新型加密标准。1997年4月，NIST开始公开征集AES算法，要求AES是一个非保密的、公开披露加密算法的、全球免费使用的分组密码，算法必须采用对称密码体制，最少应支持128bit的分组和128bit、192bit、256bit的密钥。1998年8月，NIST召开第一次AES候选算法会议（AES1），并公布了15个候选算法。1999年3月，召开第二次AES候选算法会议（AES2），公开了15个候选算法的讨论结果。参考AES2的讨论结果，NIST从15个候选算法中选出了5个算法：MARS、RC6、Rijndael、SERPENT、Twofish，作为进一步讨论的主要对象。

2000年4月，NIST召开第三次AES候选算法会议（AES3），对剩下的5个候选算法做进一步的分析和讨论。2000年10月2日，NIST宣布Rijndael算法当选AES，成为新一代的加密标准。AES于2001年7月正式投入使用。

当选的AES算法是由比利时人Joan Daemen和Vincent Rijmen提交的、由Joan Daemen设计的名为Rijndael的密码算法。该算法是迭代分组密码算法，其分组长度和密钥长度都可改变，该算法的扩充形式允许分组长度和密钥长度以32bit的步长，在128～256bit范围内进行特定的变化。该算法的主要优点是设计简单，密钥安装快、需要的内存空间少，在所有平台上运行良好，支持并行处理，对抗所有已知攻击。下面分别介绍AES算法的各个部分。

1.状态、密钥种子和轮数

（1）状态

各个不同的变换都在称为状态（State）的中间结果上运算。状态可以用字节的一个矩阵阵列图表示，该阵列有4行，列数记为Nb且等于分组长度除以32。因为本书主要介绍针对128bit明文分组加密，Nb=4且明/密文状态图如图2-9所示。

（2）密钥种子

由加密系统提供的原始密钥称为密钥种子，与状态类似地用一个以字节为元素的矩阵阵列图表示，该阵列有4行，列数记为Nk，Nk等于分组长度除以32。如果密钥种子的长度为128bit，Nk=4且分布图如图2-10所示。

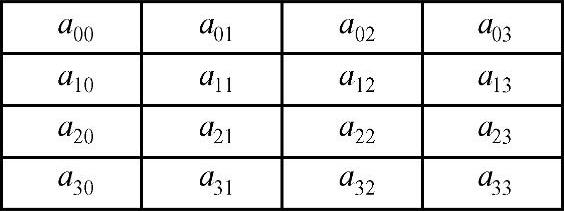
图2-9 Nb=4的状态布局

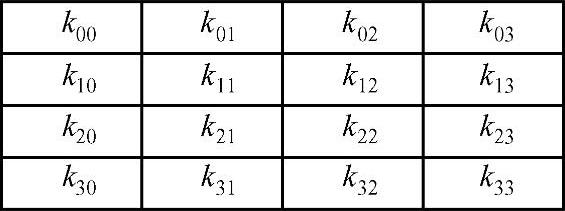
图2-10 Nk=4的密钥种子

（3）轮数

一个明文分组按a₀₀，a₁₀，a₂₀，a₃₀；a₀₁，a₁₁，a₂₁，a₃₁…的顺序映射到状态阵列中。同理，密钥种子按k₀₀，k₁₀，k₂₀，k₃₀；k₀₁，k₁₁，k₂₁，k₃₁…的顺序映射到密钥种子阵列中。当输出密文分组时，也是按相同的顺序从状态阵列中取出各字节的。将密文分组看作4Nb（4×4）维向量，每一个分量是一个字节，记为（t₀t₁t₂…t₄×_Nb-1），则密文分组的第n个分量对应于状态阵列的第（j，k）位置上的元素，其中n=j+4k，0≤j≤3。

迭代的轮数记为Nr，Nr与Nb和Nk有关，图2-11给出了Nr与Nb和Nk的关系。

图2-11 迭代轮数Nr与Nb和Nk的关系

2.轮函数

轮函数即每轮加密过程所完成的变换，它由4个不同的计算部件所组成，分别是字节代替（ByteSub）、行移位（ShiftRow）、列混合（MixColumn）、加密钥（AddRoundKey）。

（1）字节代替

将状态阵列的每个字节做相同的变换，该变换由以下两个子变换所合成：

1）首先，将字节看作GF（2⁸）上的元素，映射到自己的乘法逆；00字节映射到它自身。(www.xing528.com)

2）其次，将字节做（GF（2⁸）上的、可逆的）仿射变换，如图2-12所示。

图2-12 仿射变换

以上两个子变换合成的实现，采用一个8bit输入与8bit输出的S盒。

（2）行移位

将状态阵列的各行进行循环移位，不同的状态行的位移量不同。第0行不移动，第1行循环左移C₁个字节，第2行循环左移C₂个字节，第3行循环左移C₃个字节。位移量的选取与Nb有关。

（3）列混合

将状态阵列的每个列视为系数在GF（2⁸）上、次数小于4的多项式，被同一个固定的多项式c（x）进行模x⁴+1乘法。当然，要求c（x）是模x⁴+1可逆的多项式，否则列混合变换就是不可逆的，因而会使不同的明文分组具有相同的对应密文分组。Rijndael的设计者所给出的c（x）为（系数用十六进制数表示）：

c（x）=03x³+01x²+01x+02

c（x）是与x⁴+1互素的，因此是模x⁴+1可逆的。由前面的讨论可知，列混合运算可表示为GF（2⁸）上的可逆线性变换：

这个运算需要做GF（2⁸）上的乘法，但由于所乘的因子是3个固定的元素02、03、01，所以这些乘法运算仍然是比较简单的。

（4）加密钥

将单轮子密钥阵列简单地与密文阵列进行比特“异或”。这里要求子密钥阵列与密文阵列是同阶的。

Rijndael密码算法对应的整体流程图如图2-13所示，简单说明如下。

1）Rijndael（State，CipherKey）：该算法完成Rijndael加密。其中的State表示明文以“状态”的形式输入，CipherKey表示种子密钥。

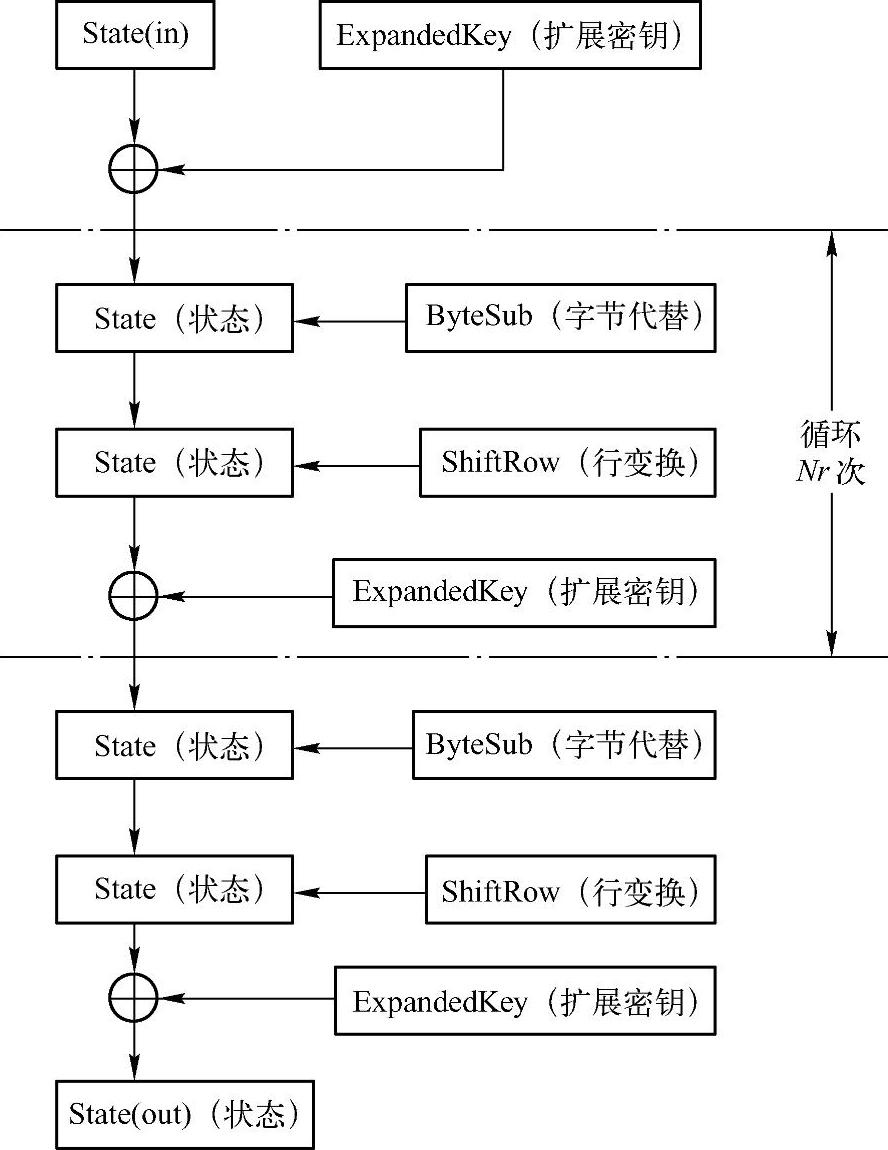
图2-13 AES加密算法流程图

2）KeyExpansion（CipherKey，ExpandedKey）：该函数主要完成密钥扩展的功能，将种子密钥（16B，4字）扩展成11组加密密钥，每组密钥的长度等于明文状态的长度。其中CipherKey表示种子密钥，ExpandedKey表示加密密钥。

3）AddRoundKey（State，ExpandedKey）：该函数主要完成初始加密钥即对明文在进行轮变换之前，进行一次简单的密钥加变换。

4）Round（State，ExpandedKey+Nb*j）：该函数主要完成轮变换，是Rijndael加密的核心部分，输入的参数分别是算法中间的结果和对应该轮的加密密钥。

5）FinalRound（State，ExpandedKey+Nb*Nr）：该函数完成最后一轮变换，它与前面由密钥长度决定轮数的循环中的轮变换的唯一不同是少了列混合（MixColumn）。