经典密码学中的置换加密方法

在历史上，加密方法被分成两大类：代换密码和置换密码。这里简要地介绍这两种密码，以作为现代密码学的背景知识。另外，一次一密作为代换密码中理想的加密方案，由于量子密码系统的研究突破，也逐渐转向实用，这里也一并介绍。

1.代换密码

在代换密码（Substitution Cipher）中，每个字母或者每一组字母被另一个字母或另一组字母来取代，从而将原来的字母掩盖起来。最古老的密码之一是凯撒密码，它因为来源于Julius Caesar而得名。在这种方法中，a变成D，b变成E，c变成F，…，z变成C。例如，attack变成DWWDFN。在例子中，明文以小写字母给出，密文则使用大写字母。

凯撒密码的一种通用方案是，允许明文字母表被移动k个字母，而并不总是移动3个字母。在此情况下，k变成了这种循环移动字母表的通用加密方法的一个密钥。

接下来的改进是，让明文中的每个符号（为了简化起见，这里假设为26个字母）都映射到其他某一个字母上，例如

明文：abcdefghijklmnopqrstuvwxyz

密文：QWERTYUIOPASDFGHJKLZXCVBNM

这种“符号对符号”进行代换的通用系统被称为单字母表代换（Monoalphabetic Substitution），其密钥是对应于整个字母表的26字母串。对于上面的密钥，明文attack被变换为密文QZZQEA。

初看起来，这似乎是一个非常安全的系统。因为虽然密码分析者了解通用的系统（即字母对字母的置换），但是，它不知道到底使用哪一个密钥，而密钥的可能性共有26！≈4×10²⁶种。与凯撒密码不同的是，要试遍所有可能的密钥是不可行的。即使一台计算机测试每个密钥只需1ns，试遍所有的密钥也需要10¹⁰年时间。

然而，只要给出相对少量的密文，就可以很容易地破解该密码。基本的攻击手段利用了自然语言的统计特性。例如，在英语中，e是最常见的字母，其次是t、o、a、n、i等。最常见的双字母组合（或者两字母连字）是th、in、er和an。最常见的三字母组合（或者三字母连字）是the、ing、and和ion。

密码分析者为了破解单字母表密码，首先计算密文中所有字母的相对频率，然后，试探性地将最常见的字母分配给e，次常见的字母分配给t，接下来查看三字母连字，找到比较常见的形如tXe的三字母组合，这强烈地暗示着其中的X是h。类似地，如果模式thXt出现得很频繁的话，则Y可能代表了a。有了这些信息以后，就可以查找频繁出现的形如aZW的三字母组合，它很可能是and。通过猜测常见的字母、双字母连字和三字母连字，并且利用元音和辅音的各种可能组合，密码分析者就可以逐个字母地构造出试探性的明文。

另一种做法是猜测一个可能的单词或者短语，例如，考虑以下这段来自于一家会计事务所的密文（5个字符分成为一组）：

CTBMN BYCTC BTJDS QXBNS GSTJC BTSWX CTQTZ CQVUJ

QJSGS TJQZZ MNQJS VLNSX VSZJU JDSTS JQUUS JUBXJ

DSKSU JSNTK BGAQJ ZBGYQ TLCTZ BNYBN QJSW

在会计事务所的消息中，一个可能的单词是financial。在financial这个单词中有一个重复的字母i，并且这两个i之间有4个其他的字母。根据这样的知识，在密文中查找相隔4个位置的重复字母，可以找到12个地方，分别在6、15、27、31、42、48、56、66、70、71、76和82位置上。然而，只有其中两个地方，即31和42，它的下一个字母（对应于明文中的n）也在正确的位置上重复。而在这两者之中，只有31有正确的a位置（考虑在financial中有两个a），所以，由此可知financial从位置30开始。以此为出发点，利用英语文本的频率统计规律可以很容易地推断出密钥。

2.置换密码

代换密码保留了明文符号的顺序，但是将明文伪装起来。与此相反，置换密码（Transposition Cipher）重新对字母进行排序，但是并不伪装明文。图2-2给出了一个常见的置换密码：列置换。该方案用一个不包含任何重复字母的单词或者短语作为密钥。在这个例子中，密钥是MEGABUCK。密钥的用途是对列进行编号，第一列是指在密钥的字母中最靠近英文字母表起始位置A的那个字母，第二列是指在密钥的字母中仅次于指定第一列字母的下一个字母，以此类推。明文按水平方向的行来书写，如果有必要的话填满整个矩阵（填充内容一般可自由设定）。密文被按列读出，从编号最低的密钥字母开始逐列读出。

图2-2 置换密码示例

为了破解置换密码，密码分析者首先要明白，自己是在破解一个置换密码，通过查看E、T、A、O、I、N等字母的频率，很容易就可以看出它们是否吻合明文的常规模式。如果是的话，则很显然这是一种置换密码，因为在这样的密码中，每个字母代表的是自己，从而不改变字母的频率分布。

接下来要猜测共有多少列。在许多情况下，从特定的环境信息中或许可以猜到一个可能的单词或者短语。例如，假定密码分析者怀疑消息中的某个地方出现了明文短语milliondollars。他观察到在密文中出现的双字母组合MO、IL、LL、LA、IR和OS是因为这个短语字母交换排列的结果。密文字母O跟在密文字母M的后面（即在第4列的垂直方向上它们是相邻的）。这可能是因为它们在短语中被一段等于密钥长度的距离所隔开。如果密钥长度为7的话，则双字母组合MD、IO、LL、LL、IA、OR和NS就会出现。实际上，对于每一个密钥长度，在密文中都会出现一组不相同的双字母组合。通过检查每一种可能性，密码分析者往往很容易就能够确定密钥的长度。(www.xing528.com)

最后的步骤是确定列的顺序。当列数比较小（如k）时，则总共有k（k−1）种可能的列对，可以对每一个列对进行检查，看它的双字母组合的频率是否与英语文本的双字母组合频率相匹配。假定最佳匹配的那一对已经有正确的位置关系了，现在用剩下的每一列尝试着跟在这一对的后面，然后检查它的双字母组合和三字母组合的频率，假定最佳匹配的那一列是正确的，通过同样的方式可以陆续找到后继的列。整个过程继续下去，直至找出可能的列顺序关系。到这时，通过检查明文就可以确定是否破解成功了（例如，如果出现milloin的话，很明显就知道错误在哪里了）。

有些置换密码接受一个固定长度的块作为输入，并产生一个固定长度的块作为输出。只要输出一个能指明字符输出顺序的列表，就可以完整地描述这样的密码。例如，图2-2中的密码可以被看成一个64字符块的密码，它的输出是4、12、20、28、36、44、52、60、5、13，…，62。换句话说，第4个输入字符a首先被输出，然后是第12个字符，依此类推。

图2-3 一次一密用法示例

3.一次一密

要想构建一个不可能被攻破的密码其实是比较容易的，相应的技术在几十年前就已经被发明出来了，首先选择一个随机位串作为密钥，然后将明文转变成一个位串。例如，使用明文的ASCII表示法，最后，逐位计算这两个串的异或（XOR）值，结果得到的密文不可能被破解。因为即使有了足够数量的密文样本，每个字符的出现概率是相等的，双字母组合的概率也是相等的，三字母组合的概率也是相等的，依此类推，这种方法被称为一次一密，不论入侵者的计算能力有多么强大，这种密码总是能够对抗所有现在和将来可能发生的攻击。

图2-3给出了一个一次一密用法的例子。首先，消息1“I love you.码，然后选择一个一次性密钥Pad1，并且与消息l进行异或得到密文。密码分析者可以试验所有可能的一次性密钥，并检查每个密钥所对应的明文。例如，图2-3中列出的一次性密钥Pad2可以被用来做试验，结果得到明文2“Elvis lives”，这个结果有点似是而非。实际上，对于每一个11字符长的ASCII明文，就有一个生成此明文的一次性密钥。也就是说，在密文中没有任何破解信息，因为总是可以得到任何一条长度正确的消息。

一次一密在理论上是非常有意义的，但是在实践中有许多缺点。首先，一次性密钥无法记忆，所以发送方和接收方必须随身携带书面的密钥副本，如果任何一方有可能被敌人捕获的话，则显然书面的密钥是一个很大的威胁，而且，可被传送的消息数据量受到可用密钥数据量的限制。另一个问题是，这种方法对于丢失字符或者插入字符非常敏感。如果发送方和接收方失去了同步的话，则从失去同步的点之后所有的数据都无效了。

随着计算机的出现，一次一密方法对于某些应用可能会变得实用起来。例如，密钥源可以是一片开头部分是几分钟真实电影片断的DVD碟片，但随后它包含了几千兆字节的密钥信息，因此不会招人怀疑。但是在发送消息之前，必须首先通过其他途径，如通过网络等，将DVD转运到接收方，为此，一次一密方法的实际使用效率将变得有限。

然而，针对如何在网络上传输一次性密钥的问题，可能通过量子密码方案予以解决，尽管这个领域现在仍然在探索中，但是截止到目前的试验非常成功。如果能够更加完美一些，而且效率又很高的话，那么，几乎所有的密码系统都可以利用一次一密方法来完成，因为一次一密方法可以被证明是绝对安全的。

以BB84协议为代表的量子密码系统（Quantum Cryptography）的物理基础是：光是以一种极小的光包（Photon，也被称为光子）的形式被传递的，并且光子具有某种特殊的属性。而且，光在通过一个偏振滤光器的时候，可以被调整到一个方向上。摄影师都知道这样一个事实，如果将一束光（即一个光子流）通过一个偏振滤光器，则该光束中的所有光子都将被偏到滤光器的轴向（如垂直方向）上。如果现在光束再通过第二个偏振滤光器，则从第二个滤光器出来的光的强度将与两轴之间夹角的余弦平方成正比，如果这两个轴相互垂直的话，则所有的光子都通不过。两个滤光器的绝对方向并不重要，关键是它们之间的夹角。

可以假定Alice和Bob在一根光纤的两端，通过这根光纤他们可以发送光脉冲。为了产生一个一次性密钥，Alice需要两组偏振滤光器，第一组滤光器是由一个垂直滤光器和一个水平滤光器组成的，这种选择被称为直线基（Rectilinear Basis）。这里的一个基只是一个坐标系统而已。第二组滤光器也一样，但是旋转45°，一个滤光器的方向是从左下至右上，另一个滤光器的方向是从左上至右下，这种选择被称为对角基（Diagonal Basis）。因此，Alice有两个基，可以根据需要快速地将这些基插入到相应的光束中。Bob也有一套与Alice相同的设备，两个人都有两组可用的基。

对于每一组基，Alice现在将一个方向分配为0，另一个方向分配为1。在下面的例子中，Alice选择垂直方向为0，水平方向为1。另外，也选择从左下至右上方向为0，从左上至右下方向为1。Alice通过明文方式将这些选择发送给Bob。

现在Alice选择一个一次性密钥，如利用一个随机数发生器来生成该密钥，然后逐位地将密钥传送给Bob，在传送每一位的时候，随机地选择其中一个基。为了发送每一位，光子枪发射出来的光子已经正确地偏振到为这一位所选择的基上。Alice将会发送图2-4a中所示的光子，给定了一次性密钥和基的序列后，用于每一位的偏振方向也唯一确定下来。像这样每次发送一个光子的数据位被称为量子位（Qubit）。

Bob并不知道Alice使用了哪些基，所以他随机地为每一个到来的光子选择一个基，如图2-4b所示。如果选择了正确的基，则会得到正确的数据位。如果选择的基不正确，则得到一个随机的位，因为如果一个光子被发射到一个与它自己的偏振方向成45°角的滤光器上，那么它将会随机地跳到滤光器的偏振方向或者垂直的偏振方向上。因此，有些位是正确的，而有些位是随机的，但是Bob并不知道哪些是正确的，Bob得到的结果如图2-4c所示。

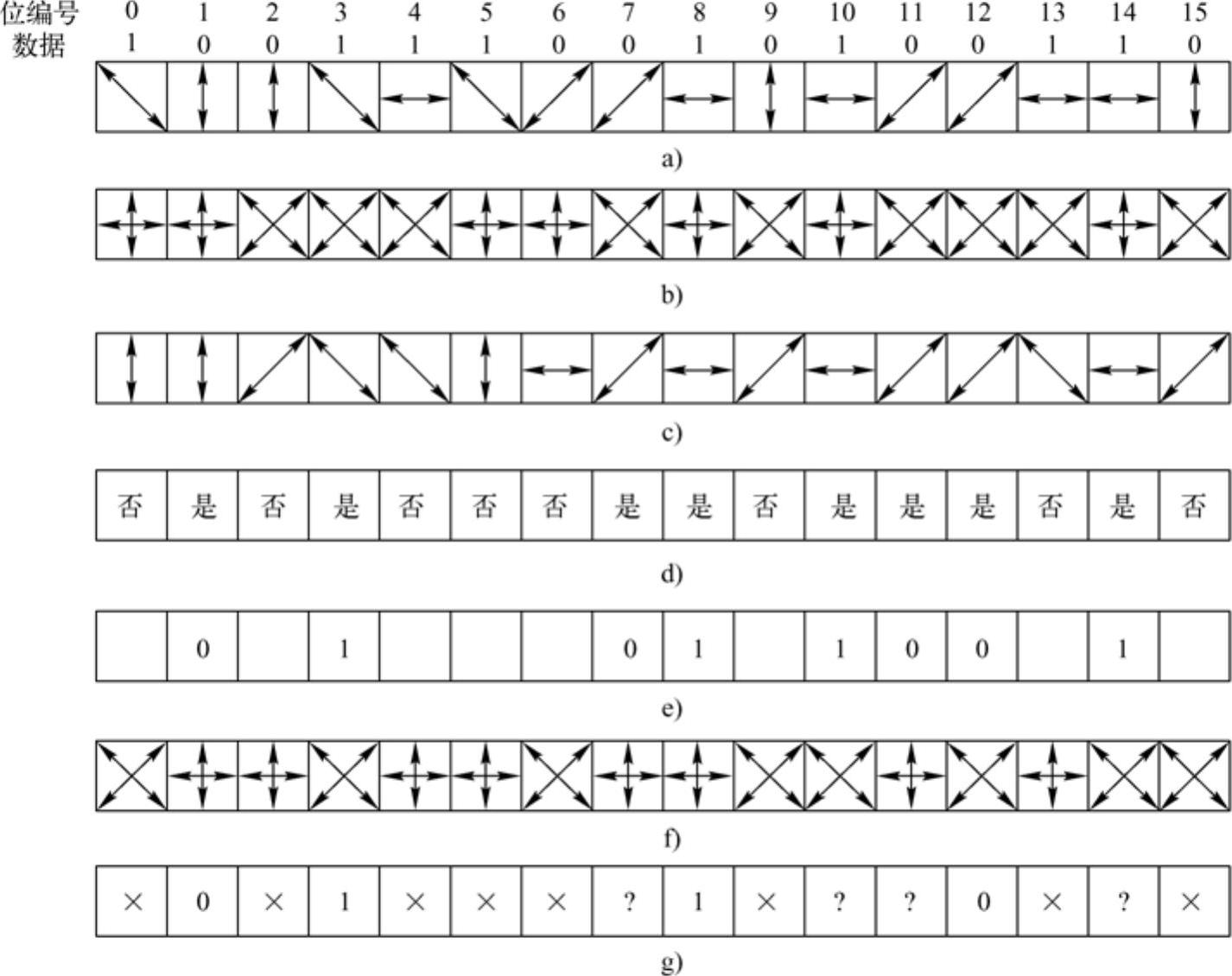
图2-4 量子密码系统示例

Bob若想如道他选择的基哪些是正确的，可以简单地告诉Alice他为明文中的每一位使用了哪个基，然后Alice告诉他，明文中哪些是正确的，哪些是不正确的，如图2-4d所示。利用这些信息，双方就可以根据正确的猜测结果获得一个位串，如图2-4e所示。平均而言，这个位串的长度将是原始位串的一半。但是，由于双方都知道这个位串了，所以他们可以将这个位串用作一次性密钥。Alice所需要做的事情仅仅是传输一个略微超过期望长度两倍的位串，于是Alice和Bob就有了一个期望长度的一次性密钥。

假设Trudy是一个入侵者，能够割断光纤，用一个主动式分接头再将光纤连接起来。Trudy可以读取两个方向上的所有数据。Trudy收到了Alice发送给Bob的光子，但是并不知道每个光子使用哪一个基，他也同Bob^一样，随机地为每个光子选择一个基，如图2-4f所示。当Bob后来用明文向Alice报告他使用了哪些基，并且Alice也用明文告诉Bob哪些基是正确的时候，Trudy也会知道得到的哪些位是正确的，哪些位是错误的。通过图2-4可知，Trudy的以下位是正确的：0、1、2、3、4、6、8、12和13。但是，根据图2-4d中Alice的应答，Trudy知道只有1、3、7、8、10、11、12和14位才是一次性密钥的组成部分，其中只有4位（即1、3、8和12）的猜测是正确的，其他的4位猜测错误，所以Trudy不知道真正传输的位是什么。

如果Trudy有办法复制光子，从而可以监视其中一个光子，并且将另一个同样的光子发送给Bob，那么，就可以将自己隐藏也来，避免被Bob发现。但是，迄今为止，人们尚未发现有理想的方法可以复制光子。尽管研究人员已经证明在超过60km距离的光纤上可以运行量子密码系统，但是装备非常复杂和昂贵。不过，量子密码学的未来仍然十分光明。