为便于企业应用,考虑应用中的近似性,我们对标准的模型作了简化处理,按照库存结构表归纳出9种模型。下面分别介绍这9种模型的近似计算公式和示意图。
(1)冗余需求模型 设R为某备件年需求量(件/年);P为某备件单件购买费用(元/件);C为某备件每批次订货费用(元/次);Q为某备件每次库存批量(件)——待优化;Q∗为经济订货量;H为单件备件平均年库存保管费用[元/(件·年)];dR为某备件保险冗余数(件);L为某备件提前订货期(天);TC为理论库存年费用;TC∗为实际库存年费用。
理论库存年费用=购买费用+订货费用+保管费用
TC=RP+RC/Q+QH/2
dTC/dQ=-RCQ-2+H/2
令导数dTC/dQ=0,则经济订货量Q∗为

重新订货点
B=R/365×L+dR
实际库存年费用
TC∗=(R+dR)P+RC/Q∗+Q∗H/2+dRH
其库存结构图如图4-8所示。

图4-8 冗余需求库存模型
【例4-1】 某零件是某设备上的关键备件,对于设备的生产运行有直接的影响,在备件的分类上,它属于AAA型备件。在库存结构上,它属于冗余需求模型来计算它的经济订货批量。通过调查和分析,已知它的年需求量为660件。单件购买时,费用是150元/件,按批来订货时,订货费用是450元/次,每次的库存批量是60件。单件的平均年库存保管费用是8元/件。根据这种零件在实际生产运行的日常磨损更换和意外故障的发生频率,得出其提前订货期为3天,保险冗余数为5件。求实际库存年费用。
解:理论库存年费用为
TC=RP+RC/Q+QH/2=(660×150+660×450/60+60×8/2)元=104190元
经济订货量为

重新订货点为
B=R/365×L+dR=660/365×3+5=10件
实际库存年费用为
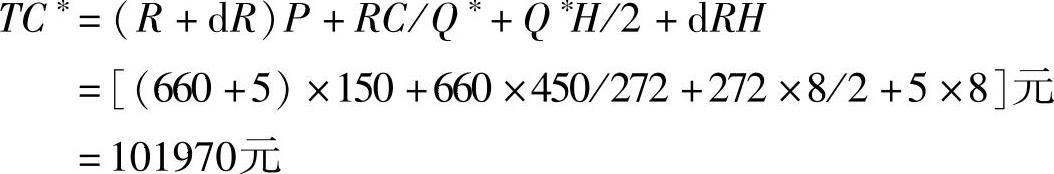
从理论和实际全年的库存总费用的比较得出,经济批量订货节省了2220元。虽说2220元并不是大数目,但这只代表了一种备件的占用金额,如果把全部的AAA型备件按照以上的计算方法来进行库存管理的话,那金额就远不止2220元,甚至有可能为企业节省上十万元、百万元的资金。
(2)一般需求模型 符号的含义同前。
理论库存年费用=购买费用+订货费用+保管费用
TC=RP+RC/Q+QH/2
dTC/dQ=-RCQ-2+H/2
令dTC/dQ=0,则最经济订货量Q∗为
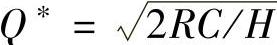
重新订货点
B=R/365×L
实际全年库存总费用
TC∗=RP+RC/Q∗+Q∗H/2
其库存结构图如图4-9所示。

图4-9 一般需求库存模型
【例4-2】 以电子厂某设备的某零件为例,它在备件的分类中属于AAC型备件,它的更换周期(订货周期)是7天,年需求量是70件,每单件购买费用是65元,每批次订货费用是300元。单件备件的平均年库存保管费是250元。经过计算得知,其提前订货期是2天,每次库存批量是6件。求实际库存年费用。
解:理论库存年费用为
TC=RP+RC/Q+QH/2=70×65+70×300/6+6×250/2=8800元
经济订货量为

重新订货点
B=R/365×L=70/365×2=0.4件
实际库存年费用为
TC∗=RP+RC/Q∗+Q∗H/2=(70×65+70×300/13+13×250/2)元=7790.4元
从上面的例子可以看出,当每次订货的备件量是13件时,它的年库存总费用是7790.4元,比每次订6件(即库存批量6件)时的年库存总费用节省了8800元-7790.4元=1009.6元。虽然每次订货的数量是增加了7件,但却减少了订货费用,从而就降低了库存费用,减少了企业流动资金的占用。
以上的计算方法同样适用于BAB、ACA等类型的备件的最经济订货批量的计算。
(3)可短缺库存模型 符号的含义同前。
理论库存年费用=购买费用+订货费用+保管费用(https://www.xing528.com)
TC=RP+RC/Q+QH/2
dTC/dQ=-RCQ-2+H/2
令dTC/dQ=0,则最经济订货量Q∗为
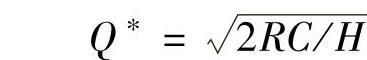
重新订货点
B=R/365×L-dR
实际库存年费用
TC∗=(R-dR)P+RC/Q∗+Q∗H/2-dRH
其库存结构图如图4-10所示。

图4-10 可短缺库存模型
(4)保险周期库存模型 设P为某备件单件购买费用(元/件);C为某备件每批次订货费用(元/次);Q为某备件每次更换批量(件);H为单件备件平均年库存保管费用[元/(件·年)];E为某备件更换周期(天);M为某备件库存时间(天);dR为备件保险冗余量(件)。
理论库存年费用=购买费用+订货费用+保管费用
即 TC=365PQ/E+365C/E+365QMH/365E+dRP+dRH=365PQ/E+365C/E+QMH/E+dRP+dRH
其中,购买费用为365PQ/E+dRP,订货费用为365C/E,保管费用为365QMH/365E+dRH。
库存结构图如图4-11所示。
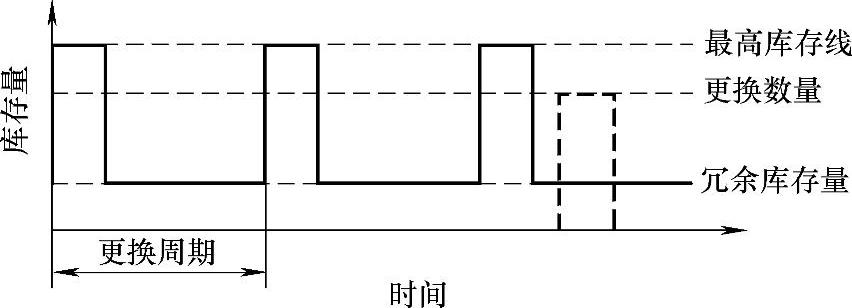
图4-11 保险周期库存模型
(5)零库存周期模型 符号的含义同(4)保险周期库存模型。
理论库存年费用=购买费用+订货费用+保管费用
TC=365PQ/E+365C/E+365QMH/365E=365PQ/E+365C/E+QMH/E
其库存结构图如图4-12所示。

图4-12 零库存周期模型
(6)短缺周期模型 符号的含义同(4)保险周期库存模型。
理论库存年费用=购买费用+订货费用+保管费用
TC=365PQ/E+365C/E+365QMH/365E-365PdR/E-dRMH/E=365PQ/E+365C/E+QMH/E-365PdR/E-dRMH/E
其库存结构图如图4-13所示。
(7)保险上下限模型 设某备件最大需求量为MAX,最低库存维持量为MIN,年需求量不明确,订货提前周期不明确,设其保险冗余量为dR。

图4-13 短缺周期模型库存结构图
库存上限即每次订货量U=MAX+dR
库存下限即提前订货点D=MIN+dR
其库存结构图如图4-14所示。
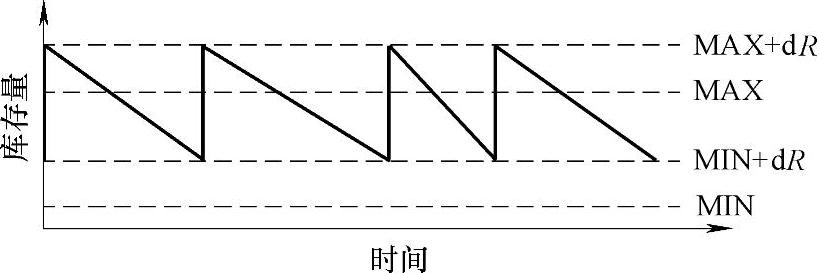
图4-14 保险上下限模型
(8)一般上下限模型 设某备件最大需求量为MAX,最低库存维持量为MIN,年需求量不明确,订货提前周期不明确。
库存上限即每次订货量U=MAX
库存下限即提前订货点D=MIN
其库存结构图如图4-15所示。

图4-15 一般上下限模型
(9)短缺上下限模型 设某备件最大需求量为MAX,最低库存维持量为MIN,年需求量不明确,订货提前周期不明确,设其允许短缺量为dR。
库存上限即每次订货量U=MAX-dR
库存下限即提前订货点D=MIN-dR
其库存结构图如图4-16所示。
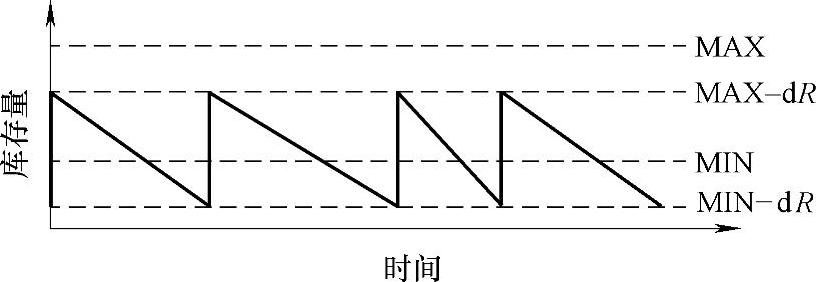
图4-16 短缺上下限模型
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




