迁设备是较差的投资方案——层次分析法评价方法

层次分析法也是一种多方案多评价因素的评价方法，又称AHP法。AHP法是在20世纪70年代被提出的，从80年代开始在我国流行。时至今日，仍有许多人对此法进行着改进和完善。AHP法是一种定性与定量评价相结合的方法，特别适用于评价因素难以量化且结构复杂的评价问题。

AHP法的基本做法是：首先把评价因素分解成若干层次，接着自上而下地对各层次诸评价因素两两比较（类似于环比评分法），得出评价结果；然后，通过计算，自下而上地把各层次的评价结果综合在评价目标下，即可得到诸系统方案的优劣顺序，供决策者决策时参考。

【例9-3】 某城市被一河流分为两部分，两岸间的交通需要改善。现提出了三个方案：再架一桥、在河床下挖一条隧道和建设渡轮码头。这三个方案中要选出最好的一个实施。因此评价目标是“最好的交通改善方案”。那么，怎样才算是最好的呢？可以提出下述四个评价因素：有效、安全、经济和环境协调。那么，如何才算有效呢？即快速、方便、舒适。安全又应怎样理解呢？即交通事故要少，营运事故、行车事故等也要少。同样，经济的含义也有几个方面。这样，就可以把该问题的三个备选方案的评价问题用图表示出来，如图9-1所示。

一般说来，要处理这样复杂的评价问题，AHP的做法是：先对问题所涉及的因素进行分类，然后构造一个各因素之间相互联结的层次结构模型。因素可分三类：第一是目标类，如上面例中的“最好的交通改善方案”；第二为准则类，即衡量各方案是否符合目标的标准，如“有效”、“快速”、“安全”、“交通事故少”等；第三是方案措施类，即实现目标的方案、方法和手段等，如再架一桥。

建立多因素多层次的评价模型是一项很细致的工作，要有丰富的知识和一定的经验，要进行认真的分析。

在具体说明AHP法的计算过程之前，先介绍一下n个因素的重要性程度的排序与其中任意两个因素重要性之比的关系。设有n个因素F₁，F₂，…，F_n，其重要性大小用ω₁，ω₂，…，ω_n表示，其中任意两个的重要性之比可排成一个n×n的矩阵A，即

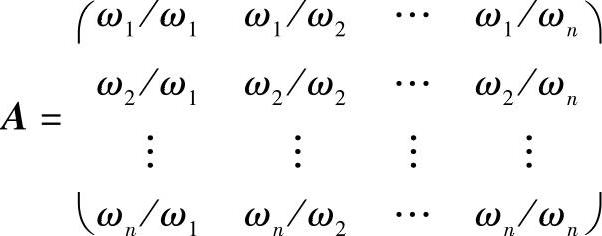
若用a_ij表示ω_i/ω_j，则矩阵A有下列性质：

（1）a_ii=1。

（2）a_ij=1/a_ji，1≤i，j≤n。

（3）a_ij=a_ik/a_kj，1≤i，j≤n。另外，若用W=（ω₁，ω₂，…，ω_n）T表示这n个因素的重要性程度向量，则有

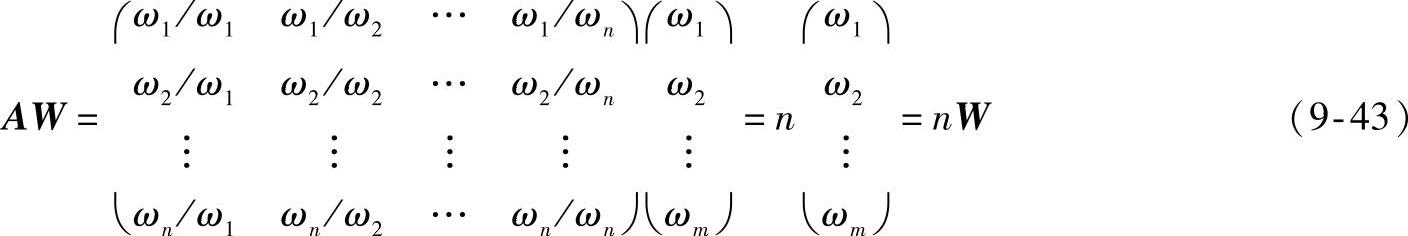
或

（A-nI）W=0

这就是说，W是A的特征向量，n是特征值。若W事先未知，则可根据决策者对n个评价因素之间两两相比的关系，主观做出比值的判断矩阵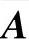。若判断矩阵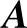具有上述性质（1）～（3），则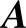具有唯一非零的最大特征值λ_max=n。然而，人们对复杂的n个因素两两比较时，不可能做到判断的完全一致性，这必然会造成特征值及特征向量中的偏差，这时AW=nW变成了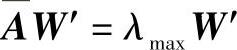，这里λ_max是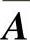的最大特征值，一般不会等于n，W′是带有偏差的重要程度向量。

为了衡量两两比较的一致性，这里定义一致性指标CI

当完全一致时，λ_max=n，CI=0；CI值越大，判断矩阵的一致性越差。一般只要CI≤0.1，就可以认为判断的一致性可以接受，否则重新进行两两比较判断。

评价因素越多，即判断矩阵的维数n越大，判断的一致性将越差，故应放宽对高维判断矩阵一致性的要求。于是引入修正值RI，见表9-4。修正后的一致性指标用CR表示，则

CR=CI/RI

表9-4 修正值RI

为了量化各因素间的两两比较结果，引入1～9标度。根据心理学家的研究结果，人们区分信息等级的极限能力为7±2，因此采用表9-5中的1～9标度。从表9-5中可以看到，在构造判断矩阵A（为了简化，省略A顶上的一横）时只要给出n（n-1）/2个判断数值就行了。除了表9-5中的1～9标度法外，还有许多别的标度法。

表9-5 1～9标度法

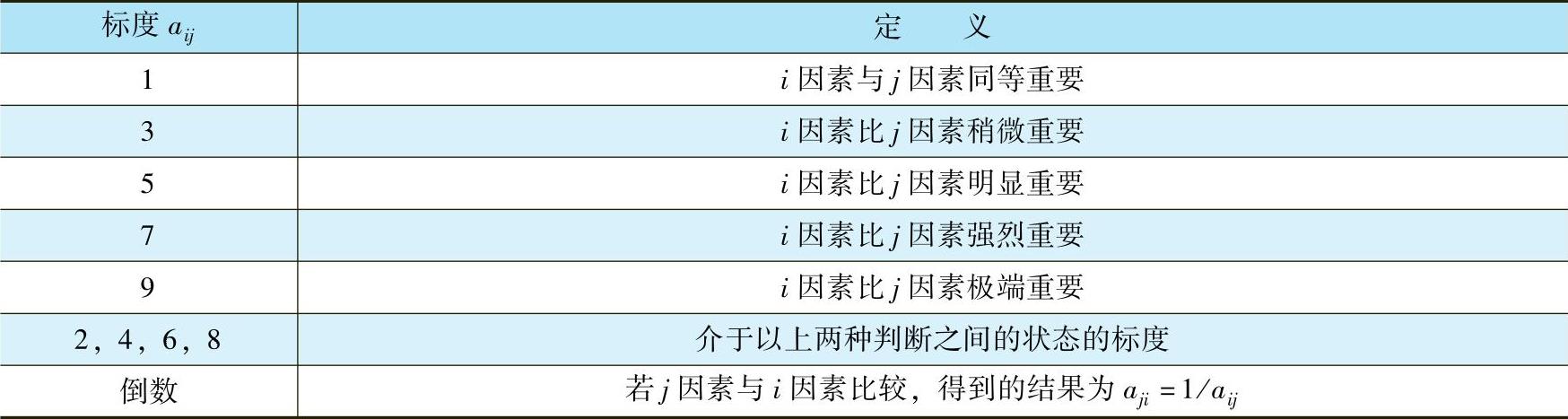
介绍完了判断矩阵及标度法之后，就可以讨论W（为了方便，省略W′右上角的一撇）和λ_max的计算了。

一般而言，AHP法中判断矩阵A的最大特征值与特征向量用近似方法计算就行了。下面只介绍其中最简单的一种。

W=（ω₁，ω₂，…，ω_N）^T

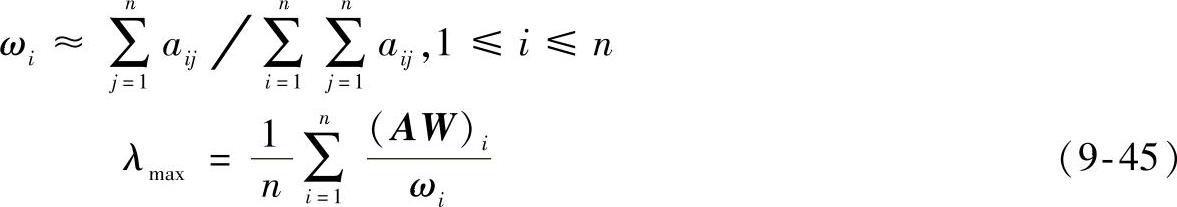
以上W只是AHP评价模型某一层次上各因素相对于一层某一具体因素的重要性向量，最终都要自下而上地组合起来，变成各系统方案相对于评价目标的重要性向量，组合方法通过下面一个具体例子来说明。

【例9-4】 某投资公司有一笔资金可用于4种方案：购置车辆、建仓库、购置自动搬运设备和购置流通加工设备。这4个投资方案哪个最好？所谓的好，是指收益大、风险低和周转快。

解 此例的AHP评价模型不难构造，见图9-4。

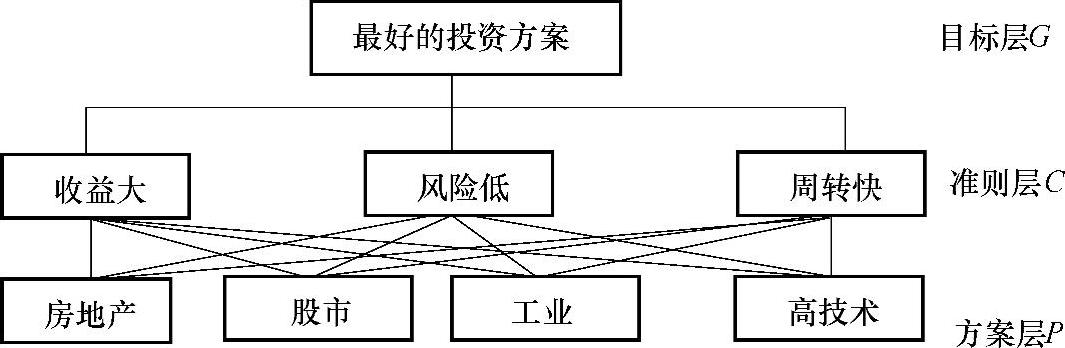
图9-4 【例9-4】的AHP评价模型

第一步，先形成准则层三个因素相对于目标层的判断矩阵G(www.xing528.com)

第二步，再分别形成方案层四个方案相对于准则层三个因素的判断矩阵C₁，C₂，C3

第三步，分别计算G，C₁，C₂，C₃的特征向量和特征值，得到

W_G=（ω₁，ω₂，ω₃）^T

其中

ω₁=（1+1/3+3）/（1+1/3+3+3+1+5+1/3+1/5+1）=0.2915

ω₂=（3+1+5）/（1+1/3+3+3+1+5+1/3+1/5+1）=0.6054

ω₃=（1/3+1/5+1）/（1+1/3+3+3+1+5+1/3+1/5+1）=0.1031

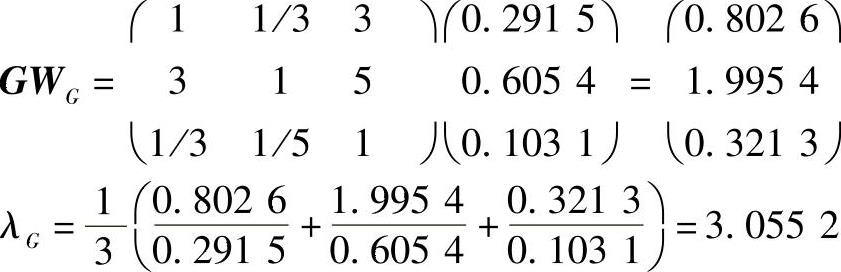
W₁=（ω₁₁，ω₁₂，ω13，ω14）^T

其中

ω₁₁=（1+1/7+3+5）/（1+1/7+3+5+7+1+9+7+1/3+1/9+1+1/2+1/5+1/7+2+1）=0.2379

ω₁₂=0.6245

ω₁₃=0.0506

ω₁₄=0.870

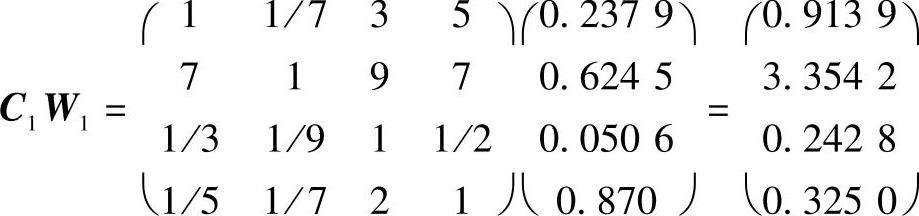
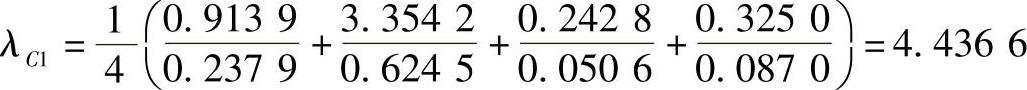
以下省去C₂，C₃特征向量W₂，W₃的计算过程，得

W₂=（ω₂₁，ω₂₂，ω₂₃，ω₂₄）^T=（0.5210，0.0619，0.3039，0.1132）^T

W₃=（ω₃₁，ω₃₂，ω₃₃，ω₃₄）^T=（0.2379，0.6245，0.0506，0.0870）^T

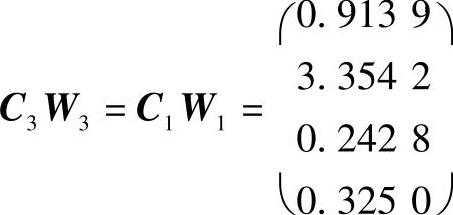
λ_C3=λ_C1=4.4366

第四步，对各级各因素判断矩阵进行一致性检验，得：

G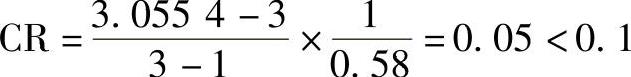：，可以。

C₁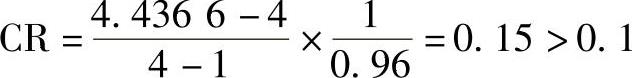：，一致性差一些，按理应重新构造判断矩阵，但在本例中，可放松要求，视为一致性检验通过。

C₂：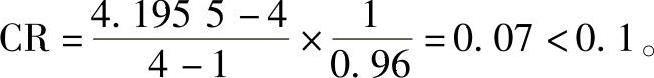

C₃：情况与C₁相同。

第五步，自下而上地组合评价结果

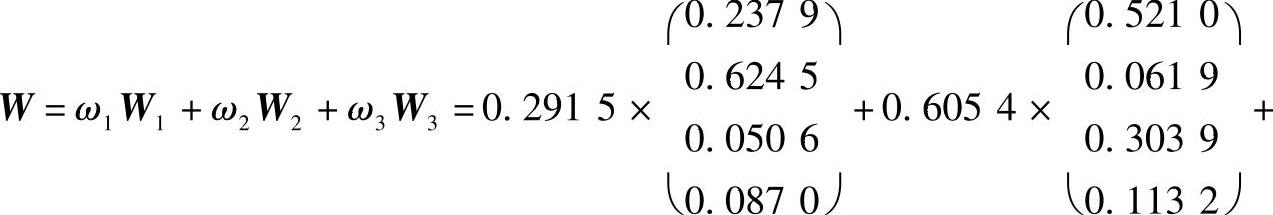
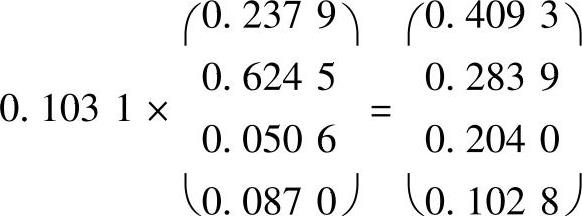
根据W中各方案的相对重要性大小可知，购置车辆是最好的投资方案，建仓库投资次之，自动搬运设备再次之，流通加工设备最差。当然，如果换一个人，而不是本书编者来构造判断矩阵，结论会有所不同。

从上面对AHP法的介绍和本节的【例9-4】可以看出，AHP法的评价结果是强烈依赖该法使用者个人的知识、经验和判断的。现在有不少人在研究如何使该法更客观。但无论如何，AHP法是一个很好的评价方法，其主要优点就是把其他方法难以量化的评价因素通过两两比较加以量化，把复杂的评价因素构成化解为一目了然的层次结构，使评价过程程序化，易于使用。正因为如此，AHP法在我国得到了广泛使用。