模糊综合评价模型下的预制构件质量级别评定

模糊综合评价就是一个模糊变换，其模型可分为一级模型和多级模型。

1.一级模型

利用一级模型进行模糊综合评价的步骤大致如下：

（1）确定评价对象的因素集。确定评价对象因素集X={x₁，x₂，…，x_n}，亦即确定指标体系。

例如，对某种住宅建筑体系进行综合评价时，可以从设计、施工、使用等方面考虑，对设计单位、施工单位和用户进行调查分析。由于三方面考虑的着眼点不同，可以建立如下评价指标集合。

施工单位：X₁={工期，造价，施工单位难易程度，人工用量}

设计单位：X₂={造价，工期，材料消耗，人工用量，使用年限，美观}

用户：X₃={使用面积，舒适程度，房租}

（2）确定评价集。评价集Y={y₁，y₂，…，y_m}又称为决策集、评语集，就是对各项指标的满足程度确定可能出现的几种不同的评价等级，例如

Y={很好，较好，一般，不好}

（3）单因素模糊评价。单因素模糊评价就是建立一个从x到y的模糊映射

f：X→f（Y）

x_i→r_i1/y₁+r_i2/y₂+…+r_im/y_m

0≤r_ij≤1；i=1，2，…，n；j=1，2，…，m

由f可诱导出模糊关系，用矩阵

～

表示，称为单因素模糊评价矩阵。

例如，针对前述某种住宅建筑体系的综合评价，可邀请若干有经验的施工管理人员、技术人员和工人从施工单位的角度进行单因素评价。比如对工期这项指标，有50%的人认为很好，30%的人认为较好，20%的人认为一般，没有人认为不好，则得出统计结果

工期（0.5，0.3，0.2，0）

若对造价、施工难易程度、人工用量三项指标统计的结果为

造价（0.6，0.2，0.1，0.1）

施工难易程度（0.3，0.2，0.4，0.1）

人工用量（0.2，0.3，0.2，0.3）

便可得到单因素模糊评价矩阵

（4）确定权重值。确定权重值是指对因素集中的各因素（即指标体系中的各项指标）的重要程度做出权重分配。

仍按上例，假定采用本章第二节中介绍的权重值的确定方法，得知从施工单位考虑的权重分配为

对应的因素集为

x_i={工期，造价，施工难易程度，人工用量}

（5）模糊综合评价。按照模糊综合评价数学模型进行模糊合成，就可得出综合评价结果。前例中，施工单位对某种住宅建筑体系的模糊综合评价为

（0.4/很好，0.2/较好，0.2/一般，0.2/不好）

由于max（0.4，0.2，0.2，0.2）=0.4，即对“很好”这一评价的隶属度最大。根据最大隶属度原则，得到施工单位对该种住宅建筑体系的评价结果为“很好”。采用同样的方法，还可以得到设计单位和用户的综合评价结果。

将三方面的综合评价提供给最高决策者参考，从而得出总的综合评价结论。

2.多级模型(www.xing528.com)

（1）问题的提出。假定有某种预制构件，其质量由9个指标x₁，x₂，…，x₉确定，构件的级别分为一级、二级、等外和废品，由有关专家、检验人员和用户组成一个单因素评价小组，得到单因素模糊评价矩阵

其中：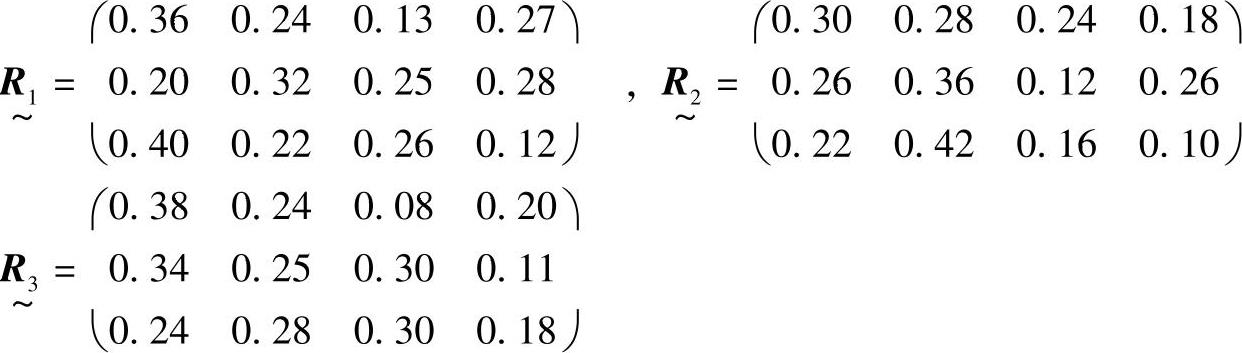

若按指标的重要性给出的权重分配为

采用一级模型进行模糊综合评价

则得不出结果。原因在于是由和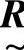的对应行列先取小后取大得到的，而权重的因素必须满足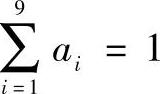，当指标数量多时，每个a_i一般来说都很小，这样在取小运算中就容易被取上；另外，当指标数量多时，要使各指标间的权重分配做到合理比较困难。

（2）利用多级模型进行模糊综合评价的一般步骤

1）将因素集X分成若干子集。因素集X按某种属性分成s个子集，记作

X₁，X₂，…，Xs

满足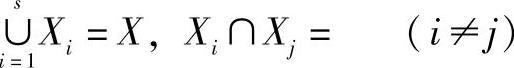。∪、∩分别为集合运算中并和交的运算符号，表示空集，即X_i与X_j不相交。

设每个子集X_i={X_i1，X_i2，…，X_ini}（i=1，2，…，s），则

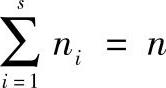
式中 n——因素集中的全部因素数目。

2）对每个子集X_i利用一级模型分别进行模糊综合评价。假定评价集Y={y₁，y₂，…，y_m}，X_i中的各指标的权重分配为，这里只要求=1。X_i的单因素模糊评价矩阵为，于是第一级模糊综合评价为

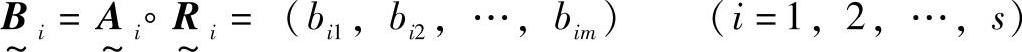
3）进行多级模糊综合评价。将每个X_i当做一个因素对待，用

作为{X₁，X₂，…，X_s}的单因素模糊评价矩阵，而每个X_i作为X中的一部分，反映X的某种属性，并按相对重要性给出权重分配，于是二级模糊综合评价为

二级模糊综合评价的模型框图如图9-2所示。

对于三级、四级以至更多级的模糊综合评价，均是在R_i的基础上再细分来完成的。此时可将

～指标利用模糊聚类分析先进行分类，然后从最低一级评价逐步做到最高一级评价，从而得出结论。

现将前面所述的某种预制构件的级别评定问题改用多级模型来解决。该问题的因素集

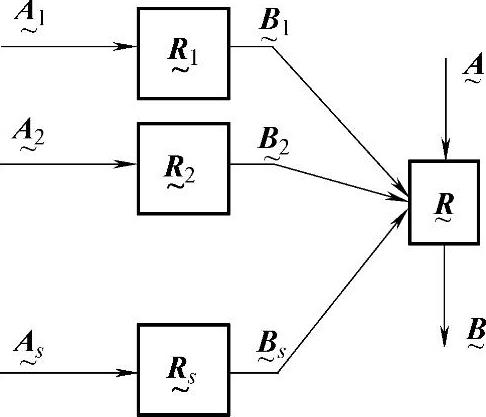
图9-2 二级模糊综合评价模型框图

X={x₁，x₂，…，x₉}，评价集Y={一级，二级，等外，废品}，单因素模糊评价矩阵为

假定按某种属性将X分为X₁={x₁，x₂，x₃}，X₂={x₄，x₅，x₆}，X₃={x₇，x₈，x₉}，它们所对应的单因素模糊综合评价矩阵分别为R～1，R～2，R～3，得出的第一级模糊综合评价结果见表9-3。

表9-3 预制构件质量级别评定的第一级模糊综合评价

取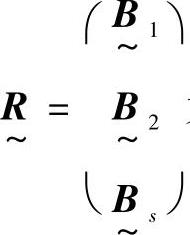为X={X₁，X₂，X₃}的单因素模糊综合评价矩阵，若采用本章第二节中权重值的确定方法得出权重分配。

第二级综合评价

根据最大隶属度原则，该种预制构件属于二等品。