模糊集：解决实际问题的推广概念

1.模糊集的概念

普通集合可以表达概念，如{1，2，…}表达了自然数这一概念。但普通集合不能表达所有的概念，例如“好”、“较好”、“适当”……就不能用普通集合表达，因为这种概念具有一种外延的不确定性。当对一个技术方案进行评价时，有时很难做出肯定或否定的回答，比如在“较好”和“一般”之间就没有一个确定的界限。这种概念外延的不确定性称为模糊性。要表达这些模糊概念，以解决具有模糊性的实际问题，就必须把普通集合的概念加以推广，这就是模糊子集（简称模糊集合）。

2.模糊矩阵的概念及运算

（1）模糊矩阵。矩阵R=（r_ij）_n×m称为一个模糊矩阵，对于任意的i≤n及j≤m都有r_ij∈[0，1]。

（2）模糊矩阵的合成。模糊矩阵合成的定义：一个n行m列的模糊矩阵Q=（q_ij）_n×m，对一个m行l列的模糊矩阵R=（r_jk）_m×l的合成Q。R为一个n行l列的模糊矩阵S，S的第i行第k列的元素等于Q的第i行元素与R的第k列元素的对应元素两两先取小者，然后再在所得的结果中取较大者，即

其中，∨、∧均为扎德算子，“∨”表示取最大，“∧”表示取最小。R也称为Q对R的模糊乘积。(www.xing528.com)

3.隶属度的概念

要对u₀是否属于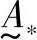做n次模糊统计试验（如对“60岁的人”是否属于“老年人”做一次意见调查），就可以得出u₀对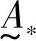的隶属频率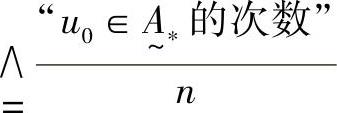。只要试验次数n足够大，该隶属频率就会稳定地趋于某一个值，这个值就称为u₀对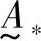的隶属度，记为

最大隶属度原则：若有i∈{1，2，…，n}，使

则认为u₀相对隶属于A～i。