净现值不确定性的概率解析

净现值不确定性的概率描述，是把净现值在不同取值范围内的可能性大小定量表示出来。一般可按以下方法和步骤来进行：

（一）估算概率

选取一个最不确定的因素作为随机变量，将这个不确定因素的各种可能结果一一列出，并分别估算各种可能结果出现的概率，并列出概率分布表。概率的估算，通常可以根据大量的历史数据进行分析，还可以通过与同类项目的比较，由项目评估人员根据经验进行估计和推算。每种不确定性因素的各种可能发生情况出现的概率之和必须等于1。

（二）确定净现值的概率分布

对于工程项目的不确定性因素来讲，它们的变化具有随机性，而一般的投资项目要受许多种已知或未知的不确定性因素影响，可以把它们看成是多个随机变量之和，故可以把各不确定性因素及净现值都视为随机变量。多数情况下可以认为（或假设）随机变量近似地服从正态分布。

由于经济学中的数据一般都是按年、季、月或日来统计的，属于离散型随机变量，其概率分布也是离散的。

（三）计算方案净现值的期望值及标准差

1.净现值的期望值

期望值是在大量重复事件中随机变量取值的平均值，换句话说，是随机变量所有可能取值的加权平均值，权数为各种可能取值出现的概率，即

式中 E（X）——净现值X的期望值；

x_i——第i种情况下的净现值；

p_i——第i种情况下出现的概率；

N——可能发生的情况总数。

某情况出现的概率是指联合概率，它等于该情况中各因素出现的概率之积。

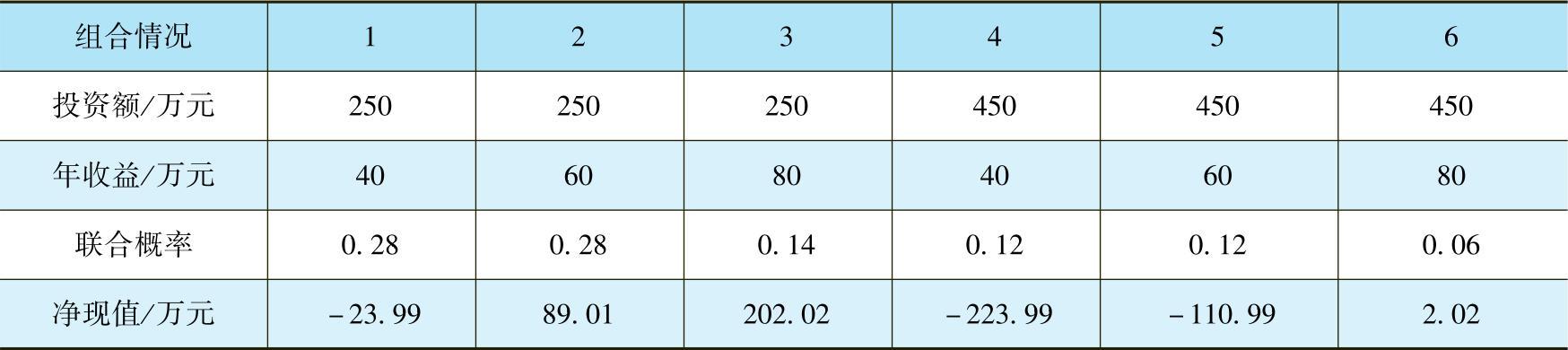
【例7-6】 已知某项目的各个参数值及其概率见表7-2，试计算方案净现值的期望值。

表7-2 项目投资额、年收益及其概率

解 投资额和年效益的不同取值共有6种组合情况，各种情况下的联合概率及相应的净现值的结果列于表7-3。

表7-3 项目投资额、年收益不同取值组合及其概率

方案净现值的期望值为

E（NPV）=-23.99万元×0.28+89.01万元×0.28+202.02万元×0.14-223.99万元×0.12-110.99万元×0.12+2.02万元×0.06=6.41万元

期望值代表了各种情况下净现值的平均值。尽管它并不是方案实际可以获得的经济效益，但它出现的次数最多，即可能性最大，据此，可以对项目的盈亏进行大致的估计。

2.净现值的标准差

既然期望值是一种平均值的描述，那么就存在有的状态取值大于平均值，有的状态又小于平均值，即在平均值上下波动。为了反映对平均值的偏离程度，用标准差来描述它。标准差是反映随机变量取值的离散程度的，或者说是反映期望值对各随机变量值的代表性大小。

一般地，假定某项目寿命期内可能发生K种状态，各种状态的净现金流序列为{y_tt=0，1，…，n}_j（j=1，2，…，k），对应于各种状态的发生概率为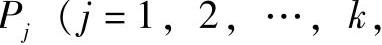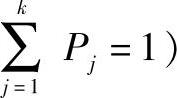，则在第j种状态下，方案的净现值为

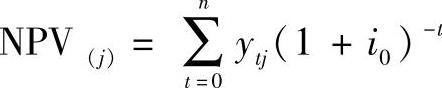
式中 y_tj——第j种状态下，第t周期的净现金流。方案净现值的期望值为

不考虑项目各年现金流量的相关性，方案净现值的标准差的计算公式为

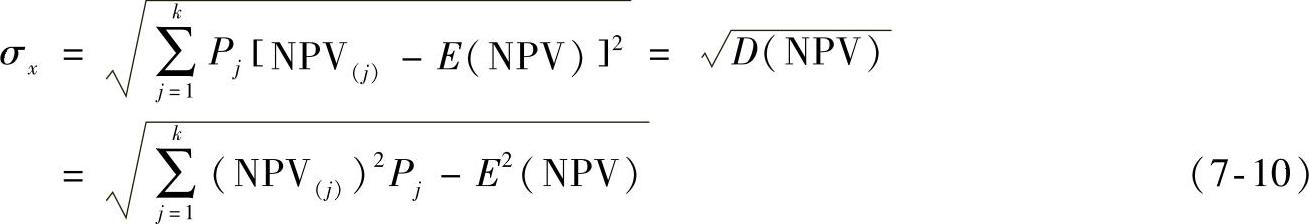
显然，标准差大的项目，其净现值不同值的离散度大，用期望值作为项目净现值的估计值的风险就大；反之，标准差小的方案，其净现值的期望值代表性大，风险也较小。因此，标准差的大小只是相对而言。对单方案来说，标准差无所谓大小，它只作为估计方案净现值取值概率的一个重要参数。而对多方案来说，标准差是比较方案风险大小的一个重要指标。

【例7-7】 已知某项目的净现值的可能取值及相应概率见表7-4，试计算其净现值的期望值及标准差。

表7-4 净现值及其取值概率

解E（NPV）=2.10万元×0.4+1.10万元×0.5+4.20万元×0.1=1.81万元

以上计算表明，上述项目最大可能的净现值为1.81万元，上下会有0.93万元的偏差。

（四）估计净现值在某一范围时的概率

对单个项目的概率分析，除应计算其期望值与标准差外，还应分析计算净现值在某一范围时的概率，由该概率值的大小可以估计项目承受风险的程度。

假定净现值取值的概率分布服从正态分布，如果已知其期望值与标准差，可以通过转换成标准正态分布的方法，计算净现值在某一范围时的概率。

根据概率论的有关原理，若连续型随机变量服从参数为_μ，σ的正态分布，则X的分布函数为

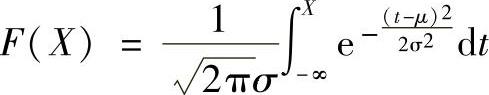
令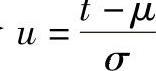，上式可化为标准正态分布函数

令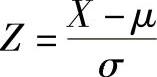，由标准正态分布表，可直接查出x<X₀的概率值

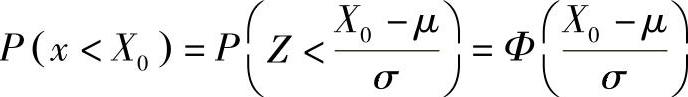
故净现值在某一范围时的概率计算公式如下：

方案净现值x小于等于某一取值X₀时的概率为(www.xing528.com)

方案净现值x大于某一取值X₀时的概率为

P（x>X₀）=1-P（x<X₀） （7-12）

方案净现值x的取值在X₁～X₂之间时的概率为

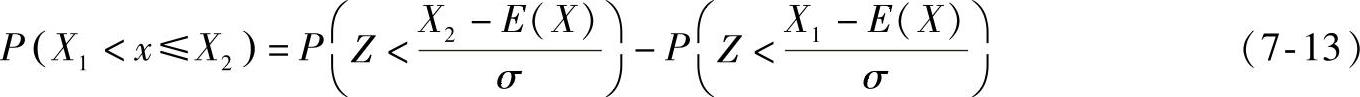
上式中的Z为标准正态随机变量。通过Z对随机变量x的代换，将x的正态分布转换为Z的标准正态分布。Z取某一范围数值时的概率可查标准正态分布表。

【例7-8】 已知某项目的净现值服从正态分布，净现值的期望值为140万元，标准差为78万元，试求：①项目净现值小于100万元的概率；②项目在经济上可行的概率；③项目净现值在180～240万元之间的概率；④项目可能获得的最大净现值。

解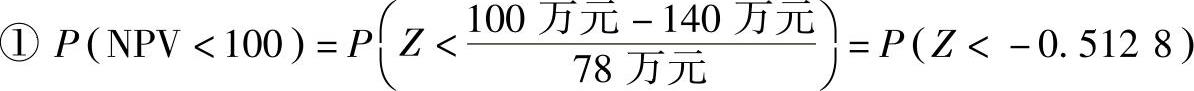

查表得

P（NPV<100）=0.3040=30.4%

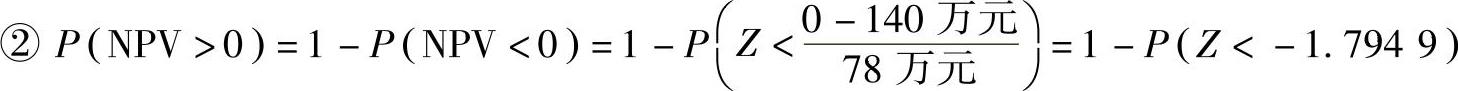
查表得

P（NPV>0）=1-0.0363=0.9637=96.37%

P（Z<0.5128）=0.6960，P（Z<1.2821）=0.9001

故

P（180<NPV<240）=0.9001-0.6960=0.2041=20.41%

④设P（Z<Y）=100%

查表得：Y=3.09

即

NPV=3.09×σ+E（NPV）=3.09×78万元+140万元=381.02万元

即

P（NPV<381.02）=100%

这就是说，项目获得的净现值在381.02万元以下的可能性为100%，或项目不可能获得比381.02万元更高的净现值。

对于随机净现值服从正态分布的投资项目，只要计算出了净现值的期望值与标准差，即使不进行如【例7-8】那样的概率计算，也可以根据正态分布的特点对方案的风险情况作大致判断。

在正态分布的条件下，由Z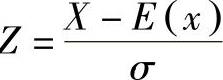，可得X=E（x）+Zσ，由于有

P（Z=0）=0.5

P（-1<Z≤1）=0.6826

P（-2<Z≤2）=0.9544

P（-3<Z≤3）=0.9974

所以有

P[X=E（x）]=0.5

P[E（x）-σ<X≤E（x）+σ]=0.6826

P[E（x）-2σ<X≤E（x）+2σ]=0.9544

P[E（x）-3σ<X≤E（x）+3σ]=0.9974

这说明，项目的净现值的实际取值为期望值的可能性为50%，实际取值在E（x）±σ范围内的可能性为68.26%，在E（x）±2σ范围内的可能性为95.44%，在E（x）±3σ范围内的可能性为99.74%。对于【例7-8】来说，项目的实际净现值在218万元范围内的可能性为68.26%，在296万元范围内的可能性为95.44%，在374万元范围内的可能性有99.74%。

在项目净现值取值的概率分布不明显，无法应用标准正态分布表进行查表计算的情况下，其概率估计还可以用表算法。其具体步骤为：将计算出来的各可能发生的事件的净现值从小到大排列起来，直到出现第一个正值为止；并将各可能发生的事件发生的概率按同样顺序加起来，求得累计概率。

【例7-9】 表7-5列出了某项目可能出现的几种净现值及相应概率，试估算项目净现值小于零的概率。

表7-5 某项目可能出现的几种净现值及相应概率

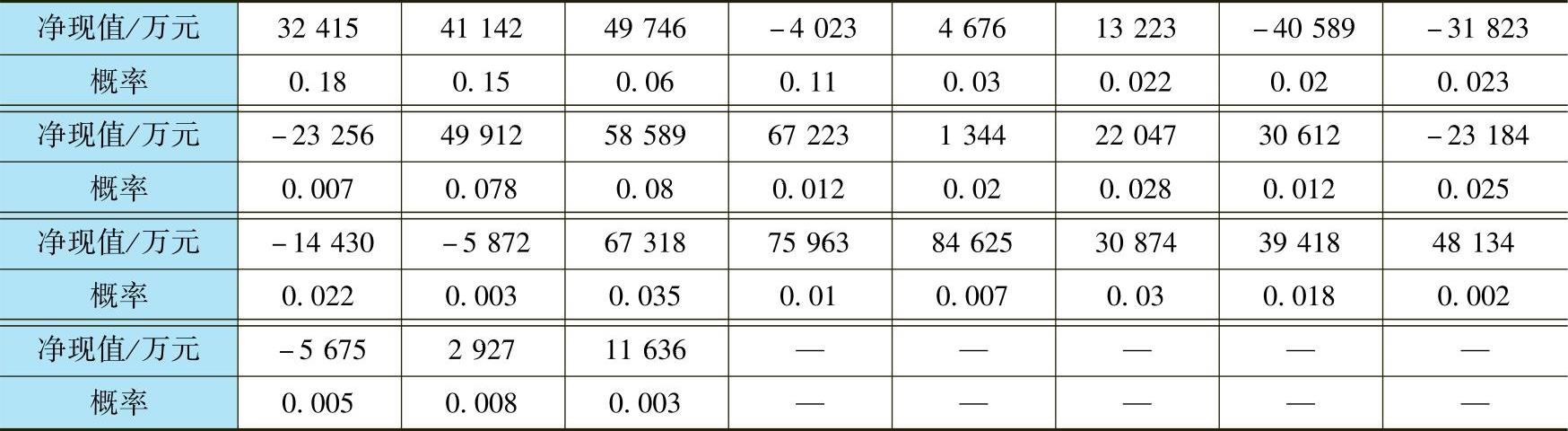
解 将NPV值按从小到大的顺序排列，直到出现第一个正值为止，并将各可能事件发生的概率按同样顺序累加起来，求得累计概率。

根据表7-6，可得净现值小于零的累计概率为

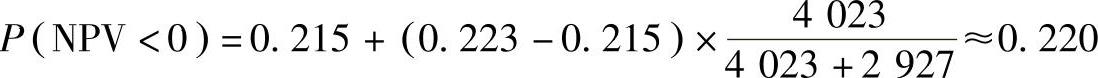
则净现值大于或等于零的累计概率为

P（NPV≥0）=1-P（NPV<0）=1-0.220=0.780

即净现值大于或等于零的可能性略低于80%，说明项目承担的风险不大。

表7-6 净现值及累计概率