如何进行多因素敏感性分析及其局限性

单因素敏感性分析可用于确定最敏感因素，但它忽略了各因素之间的相互作用。在实际中，经常出现同时有两个以上因素具有不确定性的情况，对项目所造成的风险比单因素不确定性造成的风险大。因此，在对项目进行风险分析时，还需进行多因素的敏感性分析。

多因素敏感性分析要考虑可能发生的各种因素不同变动幅度的多种组合，计算起来，要比单因素敏感性分析复杂得多。

假定项目的其他因素保持不变，仅考虑两个因素同时变化对项目经济效益的影响，称为双因素敏感性分析。其可先通过单因素敏感性分析确定敏感性较强的两个因素，然后用双因素敏感性分析判定这两个因素同时变化时对项目经济效益的影响，其具体分析步骤如下：

（1）建立直角坐标系。横轴（x）与纵轴（y）分别表示两个因素变化率。

（2）建立项目经济效益指标与两个因素变化率X、Y的关系式。

（3）取经济效益指标临界值，得到一个关于X、Y的函数方程并在坐标图上画出，即为经济指标临界线。

（4）根据上述敏感性分析图进行敏感性分析。

【例7-4】 某项目的固定资产投资I为150000元，项目建设期为1年，建成后每年年收入R为30000元，年经营费用C为2500元，该项目的寿命期为11年，回收固定资产残值S为15000元。若基准收益率为10%，试就最关键的两个因素——投资和年收入，对项目的净现值进行双因素的敏感性分析。

解

NPV=-I+（R-C）（P/A，10%，10）（P/F，10%，1）+S（P/F，10%，11）=-150000元+（30000-2500）元×（P/A，10%，10）（P/F，10%，1）+15000元×（P/F，10%，11）

设投资变化率为X，同时改变的年收入变化率为Y，则有

NPV=-150000元×（1+X）+[30000元×（1+Y）-2500元]（P/A，10%，10）（P/F，10%，1）+15000元×（P/F，10%，11）

如果NPV≥0，则该项目的盈利在10%以上。

令NPV≥0，即

8859-150000X+167565.3Y≥0

Y≥-0.0529+0.8952X

当X=0%时，Y=-5.29%，当Y=0%时，X=5.91%，即当投资增加超过5.91%，收入降低超过5.29%时，NPV<0，如图7-4所示。

由图7-4可以看出，Y≥-0.0529+0.8952X，NPV≥0，即斜线以上的区域NPV≥0，而斜线以下的区域NPV≤0，并显示了两因素同时允许变化的幅度。

若X和Y的变化幅度在±10%或±20%以内（图中方框线），出现的可能性相同时，该投资方案的NPV<0的概率等于被临界线截下的右下角的面积与相应方框总面积的比值。根据此值，可以判断出本方案净现值随投资和年收入的变化而变化的敏感性。显然，本投资方案风险较小。(www.xing528.com)

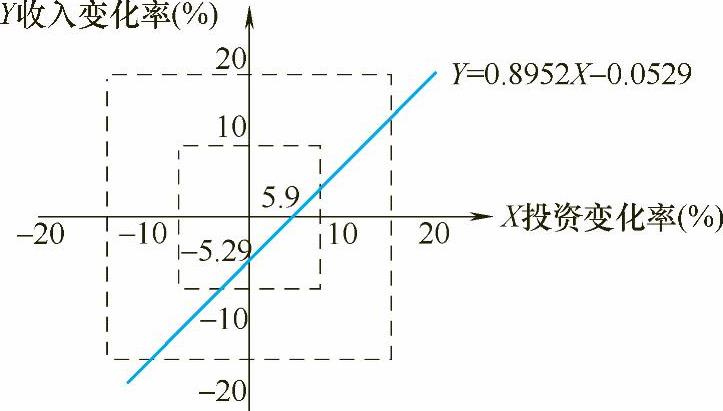
图7-4 双因素敏感性分析图

三因素敏感性分析是在项目其他因素不变的情况下，研究有三个因素同时变化时对项目经济效益的影响。它是建立在双因素敏感性分析的基础之上的。其做法是：在三个因素中选定一个因素，在某一变化范围内令该因素取不同值后得到若干条双因素临界线，然后利用这些临界线组成的敏感性分析图进行具体分析。

【例7-5】 根据【例7-4】可继续进行三因素的敏感性分析，即在投资、收入、经营成本同时变化时进行三因素的敏感性分析。有关数据同上。另设经营成本的变化率为Z，则根据

NPV=-150000元×（1+X）+[30000元×（1+Y）-2500元]（P/A，10%，10）（P/F，10%，1）+15000元×（P/F，10%，11）=8859元-150000X+167565.3Y-13963.8Z

取不同的经营成本变化率代入上式，可以求出一组NPV=0的临界线方程，即

当Z=0.5时，Y=0.8952X-0.0112

当Z=1时，Y=0.8952X+0.0305

当Z=-0.5时，Y=0.8952X-0.0945

当Z=-1时，Y=0.8952X-0.136

据此画出图7-5，得到一组临界线。由图可以看出，不同的临界线对应不同的经营费用，临界线以上的区域NPV≥0，以下的区域NPV≤0，显示了经营费用以某个幅度变化时，其他两个因素允许变化的幅度。如：Z=0.5时，Y=0.8952X-0.0112。若X=0，则Y=-1.12%；若Y=0，则X=1.25%，即经营费用增加50%时，投资允许增加1.25%，收入允许减少1.12%，这时方能盈利，否则就会亏损。

同理，可求出当经营费用变动幅度为其他值时，投资与收入允许变化的最大幅度。

敏感性分析在一定程度上就各种不确定性因素的变动对方案经济效果的影响，作了定量描述，得到了维持项目可行所能允许的不确定性因素发生不利变动的幅度。从而有助于决策者预测项目的风险情况，有助于确定在决策和实施过程中需要重点研究与控制的因素，以提高预测的可靠性。另外，在项目的规划阶段，用敏感性分析可以找出乐观的和悲观的方案，从而提供最现实的生产要素组合。

此外，敏感性分析还可以应用于方案的选择。人们可以用敏感性分析区别出敏感性大的或敏感性小的方案，以便在经济效益相似的情况下，选取敏感性小的方案，即风险小的方案。

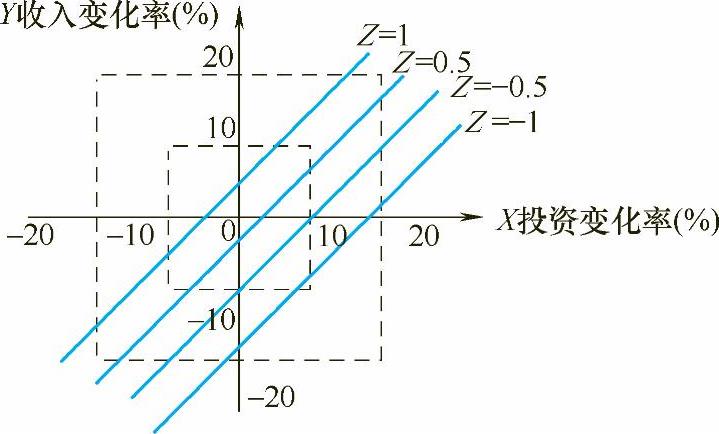
图7-5 三因素敏感性分析图

但是，敏感性分析也有其一定的局限性。它没有考虑各种不确定性因素在未来发生变动的概率。而不同的项目，各个不确定性因素发生相对变动的概率是不同的。两个同样敏感的因素，在一定的不利的变动范围内，可能一个发生的概率很大，另一个发生的概率很小。很显然，前一个因素给项目带来的影响很大，后一个因素给项目带来的影响很小，甚至可以忽略不计。这个问题是敏感性分析所无法解决的，必须借助于概率分析方法。