如何比选现金流相关型和混合型方案？

相关方案有多种类型，这里就相互依存型、现金流相关型和混合相关型三种类型相关方案的决策方法作简单介绍。

（一）相互依存型方案的比选

在多方案比选时，当某一个方案的实施要求以另一个方案的实施为条件时，这两个方案之间具有相互依存性，称为相互依存型方案。在进行比选时，常将相互依存的两个方案组合成新的方案组，再与其他方案进行比选，确定最优决策。

【例4-18】 现在有A、B、C、D四个方案，它们的寿命期均为5年，各个方案的投资及现金流量见表4-18，其中A、B、C互斥，D方案的采用与否取决于是否采用A方案，基准收益率i=10%，试做出最优决策。

表4-18 四个方案的投资及现金流量 （单位：万元）

解 由于方案A和方案D是相互依存型方案，所以可以合并成一个新的方案AD考虑，投资为300万元，年净收益为120万元。原问题就转化为在A、B、C、AD四个方案中选择最优方案。

计算各个方案的净现值

NPV_A=-100万元+40万元×（P/A，10%，5）=51.6万元

NPV_B=-140万元+50万元×（P/A，10%，5）=49.5万元

NPV_C=-160万元+70万元×（P/A，10%，5）=105.4万元

NPV_AD=-300万元+120万元×（P/A，10%，5）=154.9万元

根据净现值最大原则，方案AD是最优方案。

（二）现金流量相关型方案的比选

方案间的现金流量具有相关性又不完全互斥时，该种方案称为现金流相关型方案。这种方案的比选步骤是：首先确定各个方案之间的现金流量的关系，然后对各个方案进行重新组合，令各个组合方案之间形成互斥关系，最后利用互斥方案的比选方法进行决策。

现金流相关型方案的比选，一般可根据关联效益运用现值法和年值法等方法进行比选。

【例4-19】 根据预测，单独建铁路（方案A）或单独建公路（方案B）以及两方案同时实施的现金流见表4-19。当两方案同时实施时，由于客、货分流，两方案的收入都会下降。设i=10%，试问应如何决策？

表4-19 方案A、B的现金流量表 （单位：万元）(www.xing528.com)

解 比较方案A、方案B以及方案A+B的净现值

NPV_A=-2500万元-2500万元×（P/A，10%，2）+1500万元×（P/A，10%，48）（P/F，10%，2）=5428.3万元

NPV_B=-1000万元-1000万元×（P/F，10%，1）+600万元×（F/P，10%，2）+600万元×（P/A，10%，48）（P/F，10%，2）=3494.1万元

NPV_A+B=-3500万元-3500万元×（P/F，10%，1）-2000万元×（P/F，10%，2）+1200万元×（P/A，10%，48）（P/F，10%，2）=1480.0万元

根据净现值最大原则，在三个互斥方案中，A方案的净现值最大且大于零（NPV_A>NPV_B>NPV_A+B>0），故应选择A方案。

（三）混合型方案的比选

混合型方案是实际工作中最常遇到的问题。混合型方案分为有资金约束和无资金约束两种。当有资金约束时，可以采用混合项目互斥组合法；当无资金约束时，只要从各互斥方案中选择净现值大于零且最大的方案即可。

互斥方案组合的基本思路是：由于各个方案的现金流量之间相互影响，对现金流量之间具有正影响关系的方案，等同于独立方案看待，对相互之间有负影响关系的方案，等同于互斥方案看待。根据方案之间的关系，把方案组合成互斥的组合方案。将所有可行的方案列举出来就可以用前述的互斥方案的方法来评价选定最佳的方案组合。

由于穷举了所有可能的组合，混合项目的互斥组合法总能够保证得到已知条件下的最优组合（即总净现值最大组合）。但是，当独立项目的个数较多时，或者每个互斥项目内的互斥方案数目较多时，其组合方案数目将十分庞大。

【例4-20】 某公司有A、B两个投资对象，它们之间是相互独立的。每个投资对象各有两种互斥方案，数据见表4-20。基准折现率i=10%，各个方案的寿命期都为8年。当投资限额为60万元时，试问应如何选择方案？

表4-20 各个方案的现金流量 （单位：万元）

解 该投资项目可以分解成9个互斥方案，见表4-21。

表4-21 混合项目互斥组合表 （单位：万元）

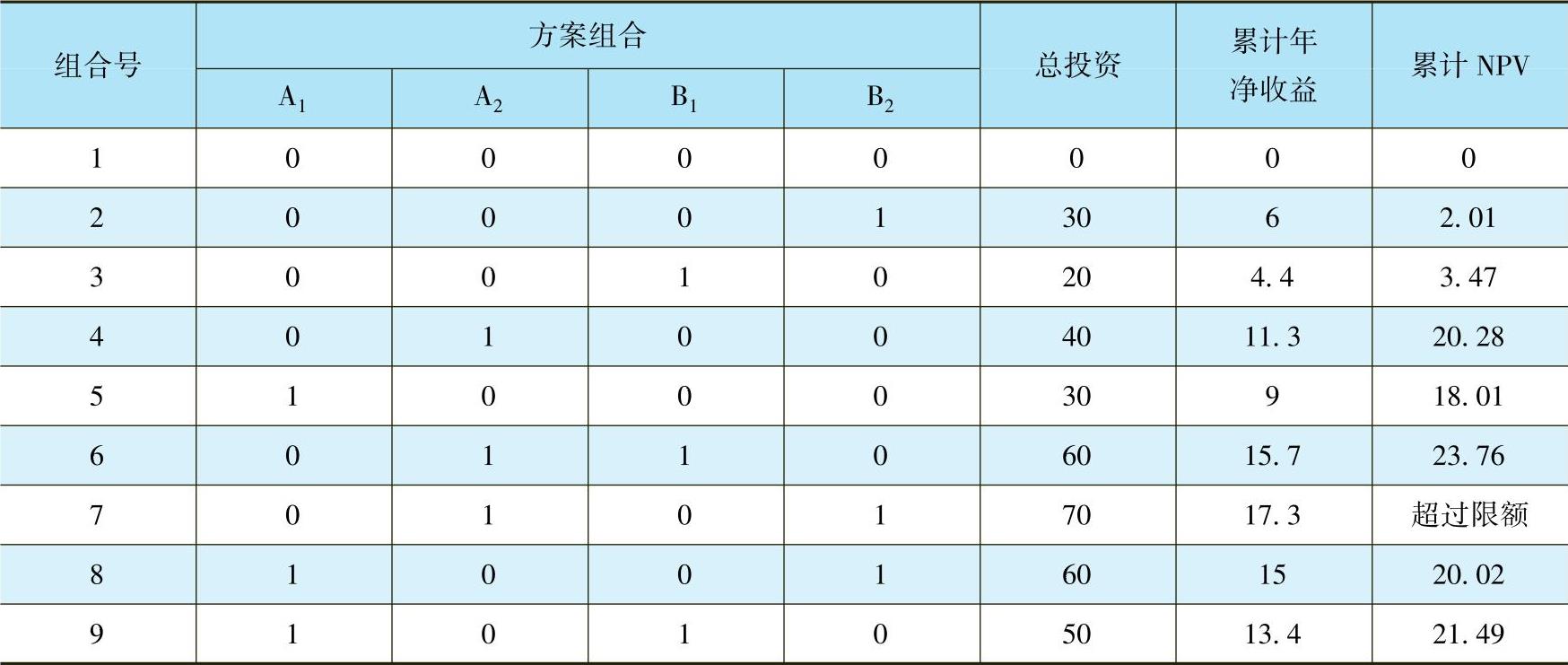
按照题意，如果投资限额为60万元，则最优组合为A₂+B₁，累计NPV为23.76万元。