(一)资金等值计算中的基本符号规定
在资金等值计算(复利计算)中的基本符号规定如下:
P——现值(本金或期初金额),即货币资金的现时价值,一般位于所取时间坐标的起点(或零期,例如建设项目开始的第一年年初)。
F——终值(未来值或复本利和),即相对于现值若干计息期后的价值,位于所取时间坐标的终点(n期末,这里,n=1,2,…)。
A——等额值,表示各期支付的金额相等,位于各期期末;当时间单位为年时,又称为等额年值或年金。
n——计息期数,其时间单位可以是年、季、月或日,具体运用公式时,要求应与复利利率的时间单位相一致。
i——计息期的利率。
(二)一次性支付的复利计算公式
资金一次性支付(又称整付),是指支付系列中的现金流量,无论是流出或是流入,均在一个时点上一次性全部发生。资金一次性支付时的等值计算公式有:
1.一次性支付终值公式
如图2-3所示,已知现值为P,计息期数为n,复利利率为i,n期末的复本利和(终值)F的计算公式为
F=P(1+i)n (2-3)
式中 (1+i)n——一次性支付(整付)复本利和系数,记为(F/P,i,n),其值可查复利系数表。
于是式(2-3)可写作
F=P(F/P,i,n) (2-4)

图2-3 一次性支付时的现金流量图
【例2-1】 某企业向银行贷款100万元,如果贷款年利率按7%计,贷款期限为5年,第5年年末一次性归还本息,按复利计算,那么5年后企业应偿还的金额为多少万元?
解 按式(2-3)、式(2-4)计算
F=P(1+i)n=100万元×(1+7%)5=140.26万元=P(F/P,i,n)=100万元×1.4026=140.26万元
2.一次性支付现值公式
如图2-3所示,已知终值为F,计息期数为n,复利利率为i,则现值P为

式中 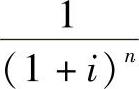 ——一次性支付(整付)现值系数,记为(P/F,i,n),其值可查复利系数表。
——一次性支付(整付)现值系数,记为(P/F,i,n),其值可查复利系数表。
于是式(2-5)可写作
P=F(P/F,i,n) (2-6)
【例2-2】 某人欲在10年后从银行拿到5万元,在年利率为10%的条件下,现在需要存入多少金额?
解 按式(2-5)计算

(三)等额支付类型
等额支付是指每个时间周期所支付的金额是相等的。等额支付时的现金流量图有两种情况,如图2-4和图2-5所示。
1.等额支付的复本利和公式
如图2-4所示,将每期的A值看做一笔整付(一次性支付)值,由式(2-3)有
F=A(1+i)n-1+A(1+i)n-2+…+A(1+i)+A (2-7)
式(2-7)的等式两端同时乘以(1+i),然后再减去式(2-7)的等式两端,有

图2-4 现金流量A与F的关系图

图2-5 现金流量A与P的关系图
Fi=A[(1+i)n-1] (2-8)
故有

式中 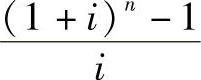 ——等额支付复利系数,记为(F/A,i,n),其值可查复利系数表。
——等额支付复利系数,记为(F/A,i,n),其值可查复利系数表。
于是式(2-9)可写作
F=A(F/A,i,n) (2-10)
【例2-3】 银行向某企业每年提供500万元的贷款,连续提供10年,每年年初注入,到第10年年末一次性还本付息,若年利率为8%,则企业应偿还的金额为多少万元?
解 现金流量图如图2-6所示。
根据现金流量图,可知第1年年初的本金在第10年年末的数值为
F1=A(1+i)n=500万元×(1+8%)10=500万元×2.1589=1079.45万元

图2-6 现金流量图
从第1年年末到第9年年末的年金,根据等额支付复利系数计算到第9年年末,再折算到第10年年末的数值为

所以第10年年末应偿还的资金总额为
F=F1+F2=1079.45万元+6743.31万元=7822.76万元
可简化为
F=A(F1/A,i,n)(1+i)=500万元×14.4866×1.08=7822.76万元
因此,若在n个周期中,每个周期开始时支出(或收入)等额值A,当年利率为i时,第n年年末的本利和为
F′=A(F/A,i,n)(1+i) (2-11)
2.偿债基金公式
由式(2-9)有

此时A的含义为,若在n期末需要积存F数额的资金用于偿还债务,且利率为i,则每期末应积存的金额就为A。于是将 称为偿债基金系数,记为(A/F,i,n),其值可查复利系数表。于是式(2-12)可写作
称为偿债基金系数,记为(A/F,i,n),其值可查复利系数表。于是式(2-12)可写作
A=F(A/F,i,n) (2-13)
【例2-4】 某人在7年后需要10000元的款项,打算每年存入银行一定数额的款项,若存款利率为8%,则每年年末应存款多少?
解 由式(2-12)有

3.等额支付的现值公式
由图2-5可知,若已知等额值为A,计息期为n,利率为i,则与该等额支付系列等值的现值P可由前述等值计算公式导出。由式(2-3)有F=P(1+i)n,由式(2-9)有 由于两F的值应相等,有等式
由于两F的值应相等,有等式
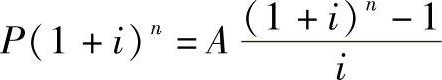 (https://www.xing528.com)
(https://www.xing528.com)
于是有

式中  ——等额支付现值系数,记为(P/A,i,n),其值可查复利系数表。
——等额支付现值系数,记为(P/A,i,n),其值可查复利系数表。
于是式(2-14)可写为
P=A(P/A,i,n) (2-15)
【例2-5】 某公司拟投资一个项目,预计建成后每年获利10万元,3年后收回全部投资的本利和。设贷款利率为10%,问该项目总投资为多少万元?
解 由式(2-14)有
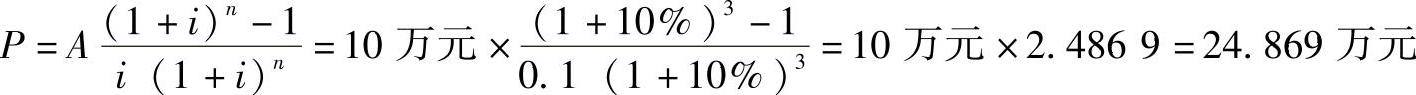
4.资本回收公式
由式(2-14)有,当P为已知而A为未知时,反求A,有计算公式

该式表明,若在期初(零期)投入资金P,在第n年年末要完全回收资本P(投资额),若每年末回收的金额相等(均为A),则只需投资额P乘以系数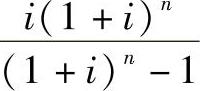 就可计算出每一年应回收的金额A,故称
就可计算出每一年应回收的金额A,故称 为资本回收系数,记为(A/P,i,n),其值可查复利系数表。于是式(2-16)可写为
为资本回收系数,记为(A/P,i,n),其值可查复利系数表。于是式(2-16)可写为
A=P(A/P,i,n) (2-17)
【例2-6】 某设备初期投资为20000元,若该设备使用年限为10年,年利率为10%,则年均设备费用为多少?
解 由式(2-16)有
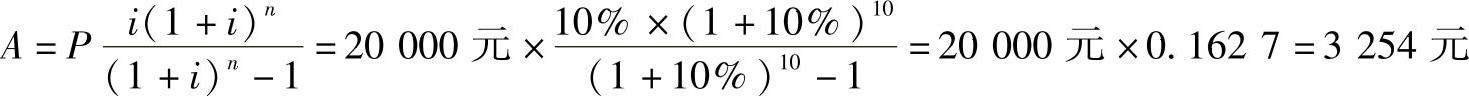
(四)特殊现金流支付系列的情况
1.等差支付系列的等值计算公式
当现金流量随着时间的延长每年(或单位时间)以等额递增(或递减)的方式进行时,便形成了一个等差支付系列。如图2-7所示,设第1年年末的支付值为A1,等差值为G,于是第2年年末的支付值为A1+G,第3年年末的支付值为A1+2G,……,至第n年年末,其支付值为A1+(n-1)G。
对于这样一个等差支付系列的等值计算,一种简便的方法是将其分解为两个与之等价的支付系列:一个是等额值为A1的等额支付系列;另一个是由0,G,2G,…,(n-1)G组成的等差支付系列,如图2-8所示。
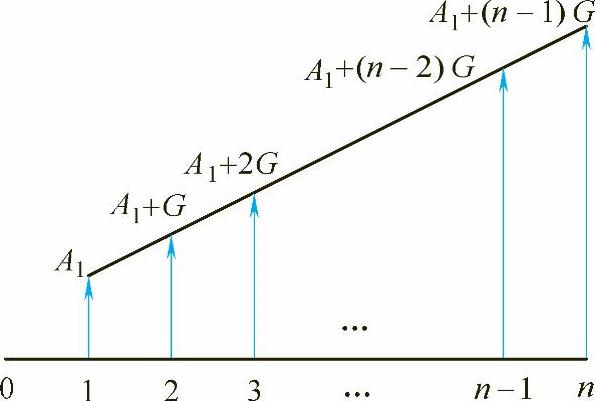
图2-7 等差支付系列现金流量图

图2-8 图2-7的分解图示
a)支付系列一 b)支付系列二
由图2-8可见,支付系列一是各年末支付值为A1的等额支付系列,其等值计算问题在前述的式(2-9)及式(2-14)已解决;支付系列二是等差值为G的等差支付系列,如果能将其转换为年末支付的等额支付系列,那么也可以利用式(2-9)及式(2-14)进行等值计算。
由图2-8的支付系列二可知,将每期末的支付值作为一笔整付(一次性支付)值看待,于是,与支付系列二等值的终值(复本利和)F2为
F2=G(1+i)n-2+2G(1+i)n-3+3G(1+i)n-4+…+(n-2)G(1+i)+(n-1)G (2-18)
式(2-18)两端同时乘以(1+i)再减去式(2-18)两端,有
F2i=G(1+i)n-1+G(1+i)n-2+G(1+i)n-3+…+G(1+i)2+G(1+i)+G-nG (2-19)
由式(2-7)可见,式(2-19)可写成
F2i=G(F/A,i,n)-nG (2-20)
故有

因有
A2=F2(A/F,i,n) (2-22)
故有


式中  ——等差系列等额支付系数,记为(A/G,i,n),其值可查复利系数表。
——等差系列等额支付系数,记为(A/G,i,n),其值可查复利系数表。
于是式(2-24)可写为
A2=G(A/G,i,n) (2-25)
式(2-24)表明,以等差值为G的前述支付系列二与等差年值A2的支付系列“等值”。求出A2后,将其与A1相加,就可得到等额年值A,即
A=A1+A2 (2-26)
有了等额年值A后,与图2-7的支付系列等值的复本利和F、现值P即可分别用式(2-9)和式(2-14)计算。
【例2-7】 有一机械设备,在使用期限5年内,其维修费在第1、2、3、4、5年末的金额分别为500元、600元、700元、800元和900元,若年利率以10%计,试计算该项费用的终值F和现值P。
解 由题意有A1=500元,G=100元,n=5,i=10%;将其分解为一个等值额为A1的等额支付系列和一个等差支付系列,其中F1和F2可由式(2-9)和式(2-21)得出。

则F=F1+F2=4157.65元
其对应的现值P为

2.等比支付系列的等值计算公式
如图2-9所示,当现金流量值每期以某一固定的百分率增加(或减少)时,就构成了一个等比支付系列,例如交通量逐年增加的百分率,原材料价格上涨的百分率等。在涉及这一类问题的支付情况并按复利计算时,就可以用等比支付系列的等值计算公式进行计算。在图2-9中,第t期期末的值为At,式中,At为第t年年末的现金流量值;A1为第一年年末的现金流量值;j为每年递增(或递减)的百分率。
按式(2-18)和式(2-22),将每期末的值作为整付值,转换为现值,则有
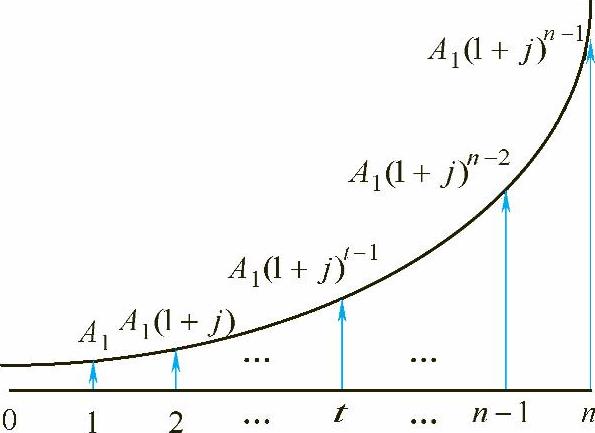
图2-9 等比支付系列现金流量图

(1)若j>i,则令 ,于是式(2-27)可变换为
,于是式(2-27)可变换为

将(1+w)还原为 ,有
,有

(2)若j<i,则令 ,代入式(2-27),经演算有
,代入式(2-27),经演算有

(3)若j=i,由式(2-27)有
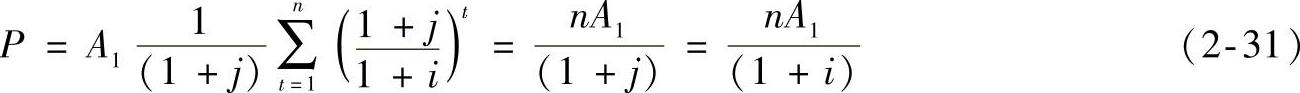
【例2-8】 某公司拟投资一种产品,估算投资额需要1200万元,该产品完成后的第一年净收益为150万元,预测产品的销售年增长率为4%。若利率i=10%,问在10年内能否完全回收投资?
解 由题意可知产品的销售年增长率为4%,即有净收益的年增长率也为4%,于是有i=10%,j=4%,A1=150万元,n=10年,由式(2-30)有净收益现值
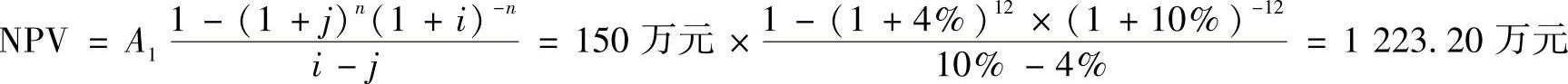
由于NPV>1200万元(投资额),故该产品在10年内能完全回收投资。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




