模型检验与估计技巧

总体回归结果显示（见表4.8），无论采用混合回归、固定效应还是随机效应模型，高级要素稀缺性变量ln（φF／φH）均在至少1%显著水平上为正，说明该变量与ln（IF／IH）之间存在显著的正相关关系，ln（φF／φH）越高（高级要素稀缺性越高），则ln（IF／IH）值越高，即一国高级要素稀缺性越高，则投资国与东道国的相对收益就越高。固定效应冗余检验与Hausman检验的结果均表明在1%以上的显著水平拒绝固定效应冗余和随机效应模型，故确定模型影响形式应为固定效应。ln（φF／φH）的偏回归系数值为0.286，这意味着要素流入国高级要素相对稀缺性增加1%的幅度，将引起要素流出国与流入国收益比值上升0.286%。与实际投入要素比ln（F／H）变量系数相比，ln（φF／φH）偏回归系数值明显更大，反映出要素稀缺性对要素流出国与流入国收益比的影响大于实际投入要素的数量比。

表4.8　要素稀缺性与直接投资收益差异的总体回归结果

注：括号内为t值，*、**、***分别表示在10%、5%和1%的水平上显著。

在确定模型影响形式为固定效应的基础上，模型可能存在三种可能的具体形式：

变系数形式：

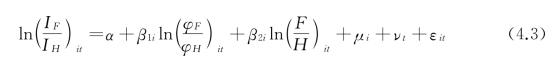
变截距形式：

不变参数形式：

构建F统计量，

通过构建变系数模型［式（4.3）］得到S1＝70.509 89，构建变截距模型［式（4.4）］得到S2＝207.2433，构建不变参数模型［式（4.5）］得到S3＝224.703，经计算得统计量F1＝51.71224，F2＝77.56836。由于F2＞F0.05（117，520），因此拒绝F检原假设H2，即拒绝不变参数模型；F1＞F0.05（78，520），拒绝原假设H1，即拒绝变截距模型，故确定本章模型应采用变系数模型形式。^[7]

为了能全面反映出要素稀缺性对收益差异影响的个体特征及其影响力的时间变化趋势，以下分别利用个体变系数与时期变系数模型进行分析。

1.个体变系数模型估计

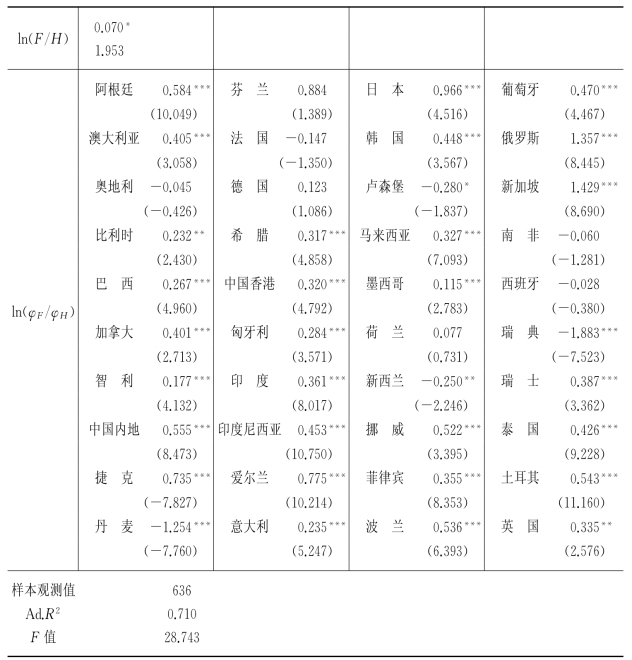
针对ln（φF／φH）构建个体变系数模型，估计结果如表4.9所示：模型拟合优度达到0.710，说明模型具有较强的解释力度。40个国家（地区）中除奥地利、芬兰、法国、德国、荷兰、南非以及西班牙等国家（地区）外，其他国家（地区）的ln（φF／φH）变量均至少在5%水平上显著。在ln（φF／φH）变量作用显著的国家（地区）中，绝大部分国家（地区）的ln（φF／φH）变量均显著为正，这表明该解释变量与被解释变量ln（IF／IH）之间均存在显著正相关关系，即一国（地区）流动性强的高级要素相对越稀缺，则要素流出国（地区）与流入国（地区）的收益比就越高。该结果验证了前文理论分析的结论，即要素稀缺性决定了要素所有者溢价能力，从而造成了直接投资收益的国家（地区）间差异。这一结果也与张幼文（2002，2005，2013）等一系列文献一脉相承。奥地利、丹麦、法国、卢森堡、南非、新西兰、瑞典、西班牙等国（地区）的ln（φF／φH）变量的偏回归系数为负，其原因可能与其自身产业结构特点及引资行业有关。以瑞典为例，其吸引外资的主要行业为医药化工，电力、燃气和供水以及木材加工与印刷等，其中医药化工的外资比重自2000年后持续下降，2000—2011年其医药化工行业FDI存量占制造业FDI存量比重由46.30%下降为30.64%，电力、燃气和供水，及木材加工与印刷行业占比则逐年上升，分别由9.74%和5.08%上升至17.73%和13.84%。^[8]与医药化工相比，这两个行业更偏向于资本和资源密集型特征，而本书的要素稀缺性指数是由劳均固定资本以及百万人中研发人员数综合而成，主要反映其资本、技术与高端人才等高级要素的相对稀缺性状况，因而可能导致该国（地区）该变量偏回归系数为负。当仅考虑劳均固定资本时，瑞典的ln（φF／φH）变量系数显著为正（详见书末附表2）。其他系数为负的国家（地区）也存在类似情况，往往是资本与资源密集型行业的引资比重上升或其主要引资行业为资本与资源密集行业。^[9]单独以劳均固定资本作为高级要素稀缺性的指标进行回归的结果，所有国家（地区）的ln（φF／φH）均为正数（详见附表2）。

表4.9　个体变系数模型估计结果

(www.xing528.com)

注：表中省略了常数项，括号内为t值，*、**、***分别表示在10%、5%和1%的水平上显著。

从ln（φF／φH）系数值大小看，在显著为正的国家（地区）中，偏回归系数值最高的国家是新加坡，其系数值为1.429，最低的国家（地区）为墨西哥，其偏回归系数值为0.115，说明样本国家（地区）中要素稀缺性变动1%，要素收益比将同向变动的幅度最低为0.115%，最高则达1.429%。这反映出要素稀缺性对直接投资收益的弹性系数存在国家（地区）间差异（见图4.10，具体排名详见附表4）。

图4.10　各国（地区）要素稀缺性指数对直接投资收益比的弹性系数

注：只涉及ln（φF／φH）变量弹性系数为正的国家（地区），其中芬兰、德国及荷兰ln（φF／φH）变量不显著。

另一个值得注意的现象是，当仅仅考虑资本要素时，所有国家（地区）ln（φF／φH）变量弹性系数均小于1（见附表2与附表3），但是当加入反映技术与人力资本的百万人中研发人员数进行考察时，部分国家（地区）的弹性系数明显上升［如新加坡、俄罗斯、日本、芬兰、爱尔兰以及捷克等国家（地区）］，这说明技术与高端人才等生产要素稀缺性的变化对这些国家（地区）直接投资收益的影响较大，增加高级要素的供给量将促使这些国家（地区）在FDI流入中获取的收益显著上升（见表4.10）。

表4.10　仅考虑资本要素与综合考虑资本、技术与人才要素后各国（地区）ln（φF／φH）系数对比

（续表）

注：奥地利、芬兰、法国、德国、荷兰、南非以及西班牙ln（φF／φH）不显著。

表4.9显示，要素实际投入比ln（F／H）在10%的水平上显著为正，系数值为0.070，即要素流出国（地区）与流入国（地区）实际投入要素相对量增加1%，将引起两国（地区）要素收益比上升0.07%，这说明实际投入要素越多，则获取的要素收益也越高。该结果既验证了前文理论推导的结论，也与一般经济规律相符。

2.时期变系数模型估计

构建时期变系数模型进一步考察ln（φF／φH）变量对收益国家（地区）间差异影响的时间变化趋势，回归结果如表4.11与图4.11所示：1996—2011年间，ln（φF／φH）历年的偏回归系数均为正数，且显著水平除2000年为10%之外，其他年份均在5%以上，这进一步证明了ln（φF／φH）与要素流出国（地区）和流入国（地区）之间收益比值之间存在正向关系。图4.11还显示，ln（φF／φH）对被解释变量影响的系数随时间推移偏离横轴的距离也越远，说明要素稀缺性变量对国家（地区）间收益比值的影响存在日益增加的趋势。流出国（地区）与流入国（地区）的要素实际投入比变量ln（F／H）不显著。

表4.11　时期变系数模型估计结果

注：表中省略了常数项，括号内为t值，*、**、***分别表示在10%、5%和1%的水平上显著。

图4.11　要素稀缺性变量作用的时期变动趋势