目标值和控制值的综合汇总

有效的控制值与被确定的、普遍的战略目标之间具有因果关系和作用关系，我们可以把它们作为战略目标的具体形式在网络PPS侧面上加以应用。图4.7对迄今已经被确认的数值进行了总结。

为了能将上述目标值和控制值之间的因果关系和作用关系阐述清楚，我们接下来会借助数学函数来说明这种相互关系。

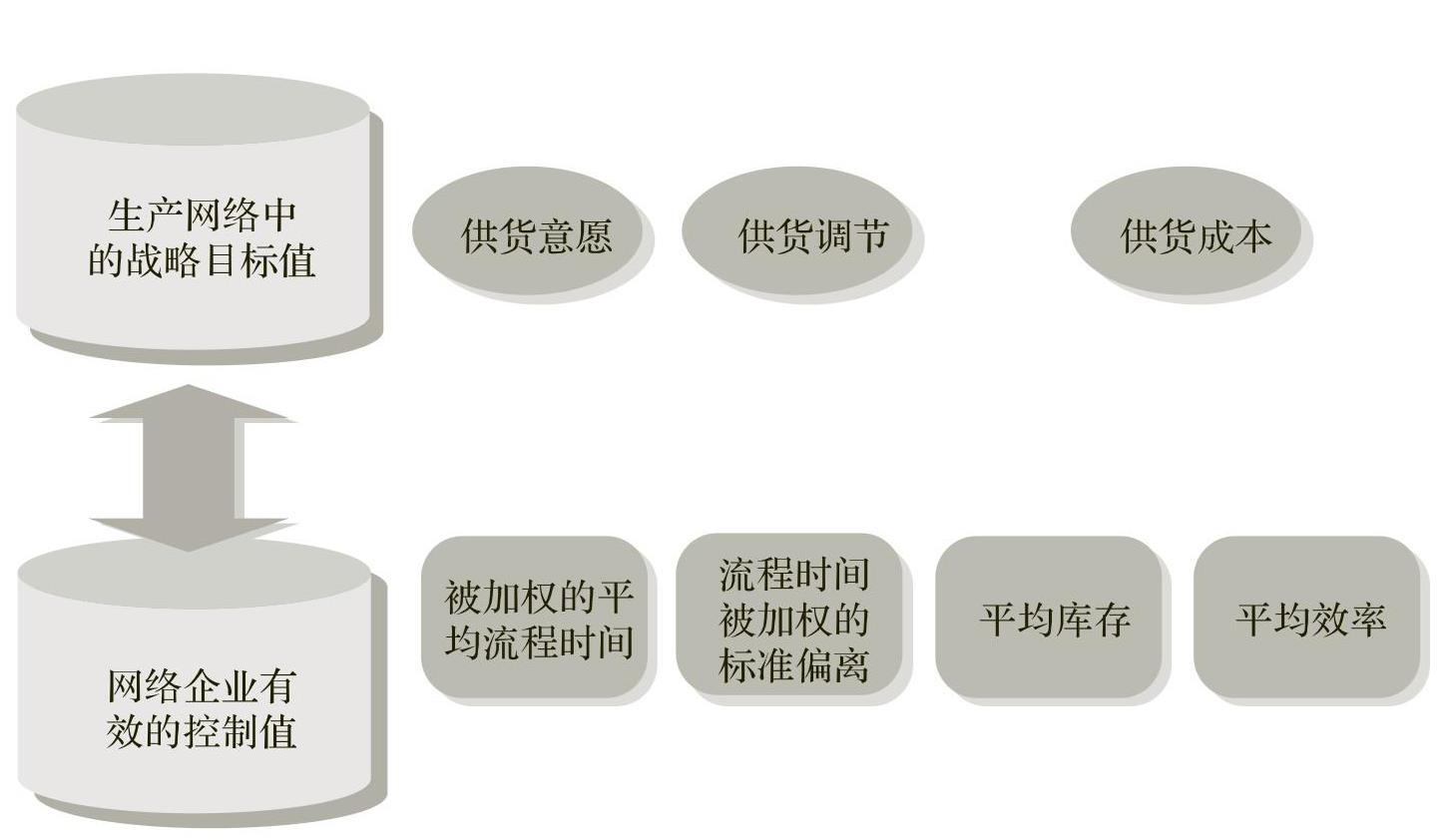
图4.7 任务：对生产网络的目标值和控制值进行的汇总

来源：作者。

作为供货意愿和供货调节基础的被加权的平均供货时间即是计划供货时间。它产生于网络企业被计划的运行时间，这一形成过程要满足的前提条件是，对于每个网络企业中的每个订单都要顾及以往的被加权的平均流程时间。这其实是一个在计划中相互连接的网络企业创造价值的过程，这些创造价值流程的计划运行时间是由最长的计划供货时间决定的，所以被加权的平均供货时间和运行时间之间存在以下相关性：

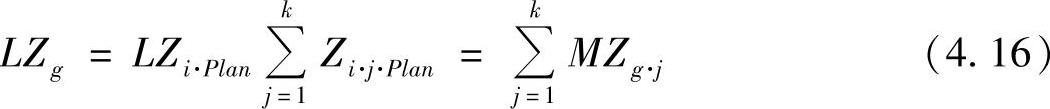
式中 LZ_g——被加权的平均供货时间；

LZ_i·Plan——网络中订单i的计划供货时间；

Z_i·j·Plan——网络企业中订单i的计划运行时间；

MZ_g·j——网络企业j中被加权的平均流程时间；

k——网络企业j的数量；

j——要完成订单i的网络企业。

作为目标值的供货灵活性与网络企业被加权的平均流程时间之间具有相关性：被加权的平均供货时间越短，同时网络企业中被加权的平均流程时间越短，就能够越早地提升订单的数量，或者提升每个订单的平均价格[见式（4.2）和式（4.4）]。

我们可以采用产能调节、引入小批量、有效的质量保证、避免长久等待以及精准的期限控制等方法来缩短供货时间。生产网络必须要努力解决供货时间较长这一问题，因为在同一时间内，有大量带有不同运行时间的订单在经过网络企业。这种情况很可能造成各个企业之间较长的过渡时间。如果不进行协同，就很容易无法实现被加权的平均供货时间，因为网络企业被加权的平均流程时间与订单实际经历的运行时间并不相符。除此以外，还会出现在介绍连续计划时已经提到过的运行时间并发症（参见2.1.2小节）。为了避免这一情况，我们在对目标值和控制值进行汇总后，会测量网络企业中的运行时间，并将其与计划的供货时间进行比较。

为了从数学角度将供货意愿与控制值联系起来，我们把上述公式用到了式（4.2）中：

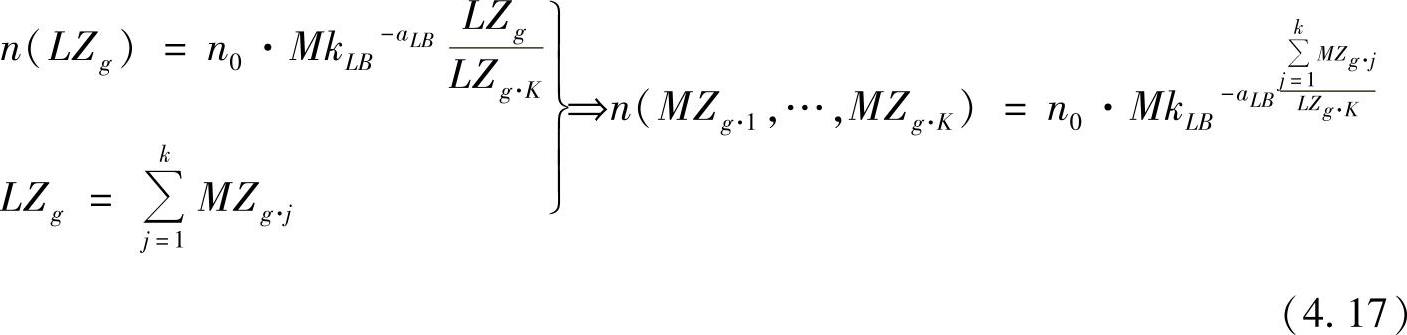
式中 n——一个计划阶段内订单的数量；

n₀——LZ_g=0时，订单的数量；

Mk_LB——当Mk_LB≥1时，供货意愿的市场常量；

LZ_g·K——竞争对手的计划平均供货时间或者被加权的平均供货时间；

LZ_g——企业自身计划的平均供货时间或者被加权的平均供货时间；

a_LB——供货意愿的比例因素；

MZ_g·j——网络企业j的被加权的平均流程时间；

k——网络企业j的数量；

j——网络企业。

在供货调整函数中，每个订单的平均价格都是结合网络企业被加权的平均流程时间得以表述的[见式（4.18）]。

式中 PR_d——每个订单的平均价格；

PR_d·0——当LZ_g=0时，每个订单的平均价格；

Mk_LA——当Mk_LA≥1时，供货意愿的市场常量；

LZ_g·K——竞争对手被加权的平均供货时间；

LZ_g——企业自身计划的平均供货时间或者被加权的平均供货时间；

a_LA——供货意愿的比例因素；

MZ_g·j——网络企业j的被加权的平均流程时间；

k——网络企业j的数量；

j——网络企业。

网络的供货成本可以借助仓储利率，并结合已规定的目标值和控制值来得以表达，不过这个过程需要遵循一个假定，那就是不管使用哪种工作体系，订单时间都足以作为比较不同订单所具备价值的尺度，而且批量大小以及安装时间都是通过订单值来得以确定的。

我们是在网络层面上对供货成本进行考察的，并且如同销售额中的数量和价格一样，是通过供货灵活性，同时借助被加权的平均供货时间得到的。如同第3章中的被加权的平均流程时间的生产特征曲线所展示的一样，被加权的流程时间同样也会对下述成本因素产生影响：

• 通过订单时间得以测量的网络的平均效率（简称：网络效率）。

• 通过订单时间得以测量的网络中的平均库存（简称：网络库存）和生产之后的供货守时性方面的负偏差。

• 供货守时性方面的正偏差，即由网络中供货时间的被加权的标准偏离得到的错误数量和由此产生的罚款。

我们可以依照式（4.9）和式（4.12）来确定平均网络库存和平均网络效率。这两个数值还可以依照式（4.15），由被加权的平均供货时间得以确定，或者通过所有平均库存和平均效率计算得到，即

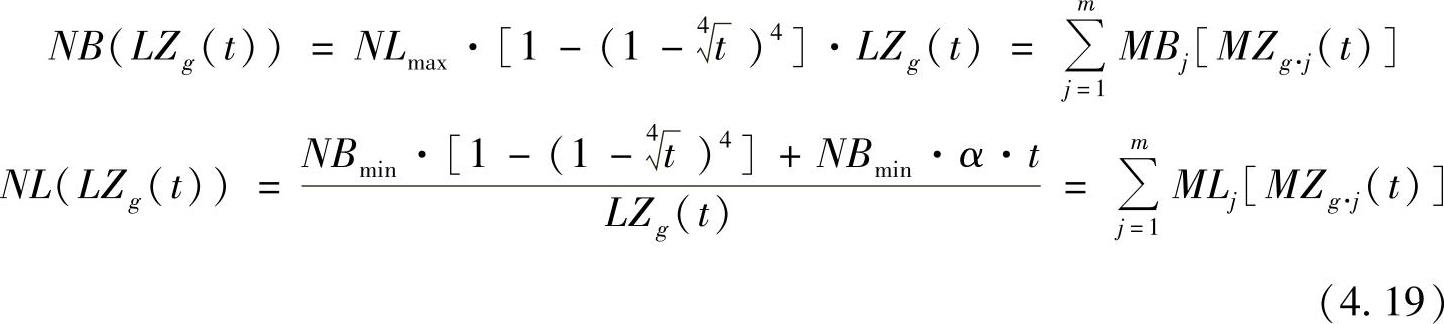
式中 NB——用订单时间来表示的平均网络库存；

NL——用订单时间来表示的平均网络效率；

NB_min——用订单时间来表示的网络中的平均最小库存；

NL_max——用订单时间来表示的网络中的可支配产能；

MB_j——用订单时间来表示的网络企业j的平均库存；

ML_j——用订单时间来表示的网络企业j的平均效率；

MZ_g·j（t）——与系统状态相关的网络企业j被加权的平均流程时间；

α——用来确定库存缓冲的给定因素；

t——系统状态，0＜t＜1；

m——网络企业的数量。

漏斗公式[见式（2.2）]可以被应用于战略型生产网络。这样，作为工作系统被加权的平均流程时间的被加权平均供货时间即是平均网络库存和平均网络效率做比得到的数值。另外，依据式（4.19），平均网络库存相当于所有平均库存的总和，而平均网络效率则相当于所有平均效率的总和。从式（4.16）还可以得出，所有被加权的平均流程时间的总和体现了被加权的平均供货时间。

由此我们得到下列用于生产网络的漏斗公式：

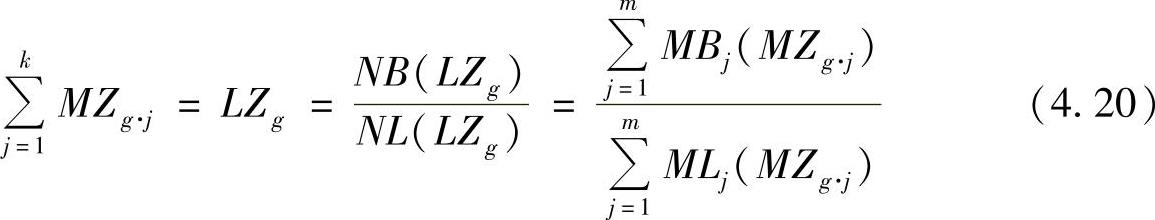
式中 MZ_g·j——网络企业j被加权的平均流程时间；

k——网络企业的数量；

LZ_g——网络被加权的平均供货时间；

NB——用订单时间来表示的平均网络库存；

NL——用订单时间来表示的平均网络效率；

MB_j——用订单时间来表示的网络企业j的平均库存；

ML_j——用订单时间来表示的网络企业j的平均效率；

m——网络企业的数量。

依照被加权的流程时间的标准偏离[见式（4.7）]来定义的网络中供货时间的被加权的标准偏离是由网络企业的被加权的标准偏离总和得到的，即

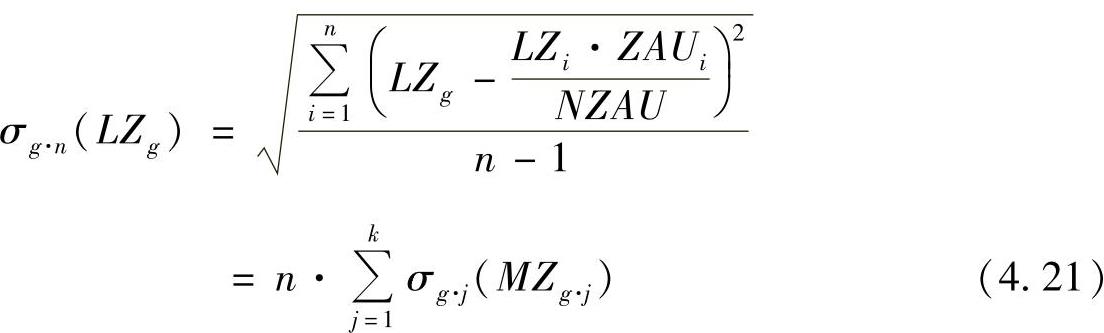
式中 σ_g·n——网络中被加权的供货时间标准偏离；

LZ_g——网络中被加权的平均供货时间；

LZ_i——订单i的供货时间；

ZAU_i——网络中订单i的订单时间；

NZAU——网络中的平均订单时间；

n——一个计划阶段内的订单数量；

k——网络企业的数量；

σ_g·j——网络企业j中被加权的平均偏离；

MZ_g·j——网络企业j中被加权的平均流程时间。

如果想要实现更高的供货灵活性，依据漏斗公式[式（4.20）]，就需要在网络平均库存恒定的情况下提高网络的平均效率，也就是对于同样多的待生产件数，需要具备更高的产能供应，这一产能供应与另外的系统状态相吻合。或者说我们要提高的不是平均网络库存，而是更高的产能。基于此，我们在可变的网络中也只能耗时较长地来调整产能。因此，我们必须对较低的负荷和库存造成的劣势进行权衡。(www.xing528.com)

如果不愿意提高可支配产能，那么可以通过降低平均网络库存[见式（4.20）]以及随之产生的平均网络效率的下降[见式（4.19）]，也就是通过降低效率来减少被加权的平均供货时间。由平均供货时间缩短而降低的平均网络效率意味着计划阶段内的效率下降。由于平均供货时间被缩短，我们必须将批量规模调整为更小，从而产生更长的安装时间和更低的效率。批量规模变小会导致机器所用工具的频繁更换，这也有可能引起质量问题。由较小批量导致的较低效率意味着因为丢掉订单和减少销售造成的机会成本[见式（4.2）]，当然我们这里没有考虑因为缩短供货时间而产生的价格优势，而且假定，额外的效率都能够全部销售出去。

下面的公式将会被用来说明我们的结论，即产出的订单，也就是产出的效率，与被分配的订单，即被销售的效率相符。如果我们利用网络中的平均订单时间，也就是平均安装和加工时间来分配产品，那么已完成的订单数量就相当于平均网络效率得到的产品。

式中 n——一个计划阶段中分配的订单数量；

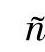——一个计划阶段中已完成的订单数量；

NL——订单时间内的平均订单效率；

P——计划阶段的长短；

NZAU——网络中的平均订单时间；

n₀——当LZ_g=0时，订单的数量；

Mk_LB——当Mk_LB≥1时，供货意愿的市场常量；

LZ_g·K——竞争对手的计划的平均供货时间或者被加权的平均供货时间；

LZ_g——企业自身计划的平均供货时间或者被加权的平均供货时间；

a_LB——供货意愿的比例因素。

产生自供货意愿函数和网络效率的被分配的订单和已完成的订单之间的紧密联系可以在应用—沟通中得到保障。

如果孤立地看效率降低，我们可以以由于被加权的平均供货时间缩短而引起的效率降低造成的相应成本为出发点。丢掉的订单数可以从计划阶段内丢掉的订单时间与网络中平均订单时间之间的商数来得到。失去的订单时间又相当于网络中可支配产能和平均网络效率之间的差异，从而产生效率降低带来的机会成本：

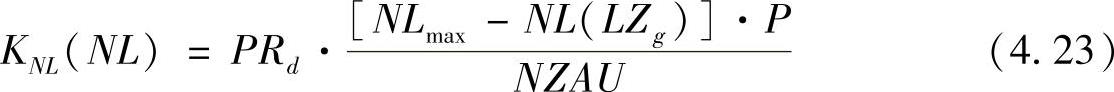
式中 K_NL——网络中效率降低造成的成本；

PR_d——每个订单的平均价格；

NL_max——用订单时间来表示的网络中的可支配产能；

NL——用订单时间来表示的平均网络效率；

LZ_g——被加权的平均供货时间；

P——计划阶段的长短；

NZAU——网络中的平均订单时间。

尽管当今的趋势是缩短供货时间，减少守时方面的偏离，而且干扰也可以通过网络中的重新计划得以较好控制，我们仍然需要就合理的PPS协同在通过提高供货灵活性实现的销售量增长以及随之缩短的平均供货时间和网络效率降低及其成本之间进行权衡。这一权衡可以在应用—沟通中进行（参见第4.2节）。

对于网络库存的成本，我们通常需要考虑两种相互对立的影响。一方面，由于存在采购费用、仓储费用以及库存可能被废弃的危险，库存会导致供货成本增加。我们进行的模拟调查还表明，较高的平均网络库存还会增加平均供货时间[见式（4.20）]，并进而间接增加被加权的供货时间的标准偏离[见式（4.21）]。我们由此得出，随着库存降低，供货守时性偏离也会减小。因为，当库存减小时，顺序交换对控制产生的影响会相应减小。

另一方面，库存可以减少被加权的平均供货时间。如果我们不是在订单到达以后才开始第一个加工阶段，并且必须完成整个生产过程，而是已经拥有了半成品，并且还必须进行组合、完善或改动等工作，那么被加权的平均时间就会整体缩短，用于生产成品和半成品的流程时间也会缩短。

当中间产品数量相对较少时，或者当我们可以从唯一一个半成品得到大量满足客户特殊需求的成品时，订单i的订单时间就可以通过库存得以缩短。这样也可以在一定程度上通过高库存量来解决供货质量问题，因为有问题的产品能够较快地得以更换。与仓储有关的决定是完全由单个的网络企业来承担的，而网络以及对网络有着重要意义的流程时间则开始于仓储层面，所以网络对仓储层面的选择使得供货时间的减少失去了重要性。

当被加权的平均供货时间缩短时，库存引起的问题可能会因为通用数据库中包含的信息而被忽略。当与订单相关的供货时间相对于计划的平均供货时间和实际平均供货时间有所缩短时，我们在计划之后才能获取相关信息，也就是说来不及在计划的平均供货时间中来完成效率的生产（参见4.1.1小节）。较短的被加权的平均供货时间可以作为网络库存的替代品，它可以降低平均网络库存，而且由于时间较短，也使得订单i的供货时间在计划之后再次缩短的可能性减小，从而用过程灵活性替代了库存灵活性。

由于被加权的平均供货时间增加而增加的平均网络库存体现了网络中的成本，这一成本主要指的是作为资本约束成本对库存中存在价值进行再投资的可能性。资本约束成本和仓储管理成本会由一个仓储管理主体从外部加以规定，并被看作是被评估的平均网络库存包含的一个因素。根据我们的假设，即库存被均匀地分配到整个网络，我们将库存的一个订单时间单位评估为每个订单时间单位供货成本的一半。为了得到每个订单时间单位的供货成本，需要用在计划阶段内已完成的订单时间单位除以计划阶段内的全部供货成本，从而可以通过下列公式得到网络库存成本：

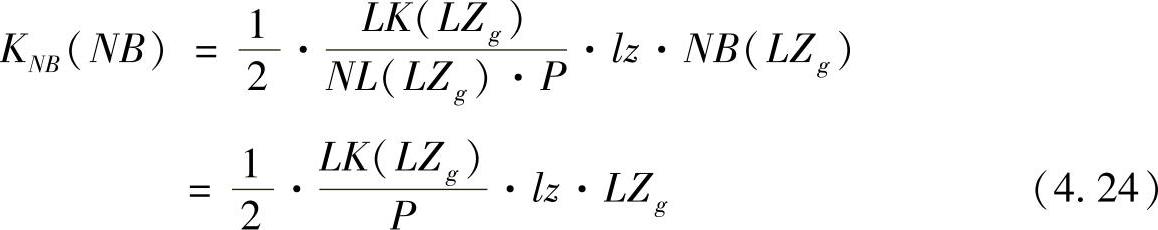
式中 K_NB——网络库存的成本；

LK——网络中的总供货成本；

NB——订单时间内的平均网络库存；

NL——用订单时间来表示的平均网络效率；

LZ_g——被加权的平均供货时间；

lz——仓储管理利率；

P——计划阶段的长短。

利用漏斗公式，我们可以像式（4.24）一样来对网络库存的成本加以描述。通过利用总供货成本（网络库存成本是其中一部分），这个方程式可以得到一个循环，这一循环是在一个总函数中对供货成本进行汇总时产生的[见式（4.27）]。

供货守时性偏离取决于能够在多大程度上遵守流程时间，即流程时间出现多大程度的分散，因为实际供货时间就是由流程时间组成的。分散程度其实是供货守时性的指示器（参见4.1.2小节），它通过被加权的供货时间的标准偏离来得以体现。供货时间的标准偏离又和网络企业的流程时间的被加权分散以及网络企业的被加权的平均流程时间长短相关[见式（4.7）]。单个网络企业则可以通过去除较短的流程时间，来降低发生守时性偏离的风险。对于流程时间的掌控不仅可以实现较短的计划平均供货时间，还可以实现较短的被加权的平均供货时间，以及较低的供货守时性偏离（较高的供货质量，参见4.1.1小节）。

如果网络对有问题的供货质量加以惩罚，那么短暂且分散的流程时间就会对供货成本产生正面影响，延迟太长时间的订单则会导致最终实际价格降低。除此之外，延迟供货让客户产生的反应还会给企业带来连带的利润损失，例如回购率的影响、对声誉的影响或者受到合约规定的惩罚。我们在此并没有考虑延迟供货对网络造成的扩散效应，或者因为缺额供货造成的整个网络的利润下降，因为应用—沟通不会允许造成这样的成本（参见3.2.2小节）。

若我们依照数学定义的相对于计划平均供货时间发生的标准偏离正常地均匀分散，那么延迟的订单会积累起来，使造成整个网络的供货时间标准偏离的平均值增大。供货时间方面的偏差会造成价格下降，这种价格下降会依照供货调节功能进行，因为订单的平均价格也是通过这一功能得以体现的[（见式（4.4）]。因而，延迟交货的订单成本可以依照下式得到：

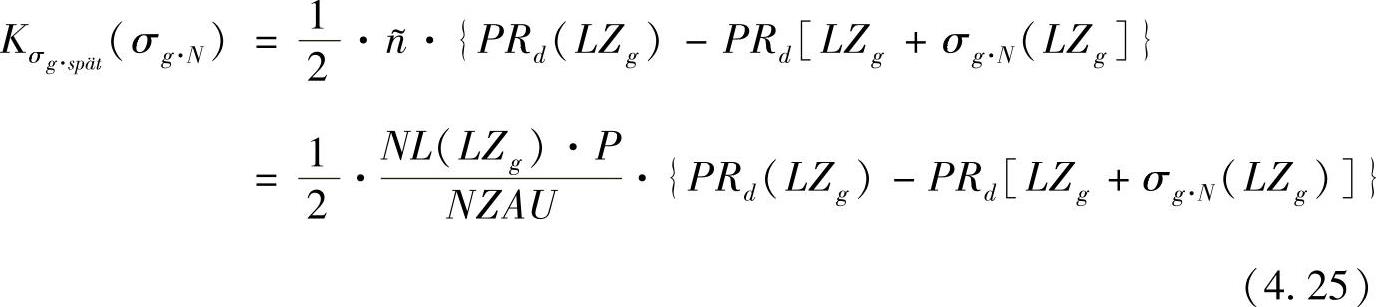
式中 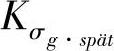——延迟订单的成本；

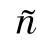——已完成的订单数量；

PR_d——每个订单的平均价格；

NL——订单时间内的平均网络效率；

NZAU——网络中的平均订单时间；

P——一个计划阶段的长度；

σ_g·N——网络中被加权的供货时间平均偏离。

供货时间的分散也会造成一半的订单提早完成。提早完成、并且无法根据供货调节被提早交付给终端客户的产品就成为仓库中的库存。由于实际供货时间是围绕计划平均供货时间正常分配地发生分散[见式（4.21）]的，所以任何一个时刻都有一半订单处于库存状态，我们会用已完成的所有订单数量去除这一半订单的总供货成本，来对其进行评估。所以网络中被加权的供货时间平均偏离并不会对提早完成的订单的成本造成直接影响：

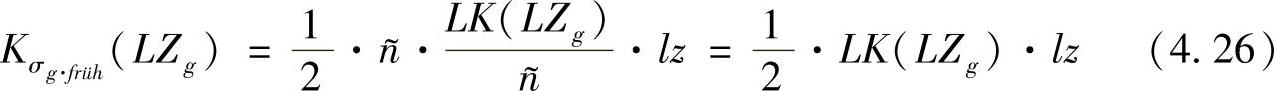
式中

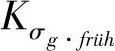——提早完成的订单的成本；

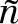——已完成订单的数量；

LK——网络中的总供货成本；

lz——仓储管理利率；

LZ_g——被加权的平均供货时间。

如果我们将上述函数[式（4.23）～式（4.26）]总结起来，就可以得到用于整个网络和整个计划阶段的供货成本函数LK，这一函数和被加权的平均供货时间相关[见式（4.27）]。我们可以利用漏斗公式用被加权的平均供货时间来替代平均网络库存和平均网络效率两者做比得到的系数。

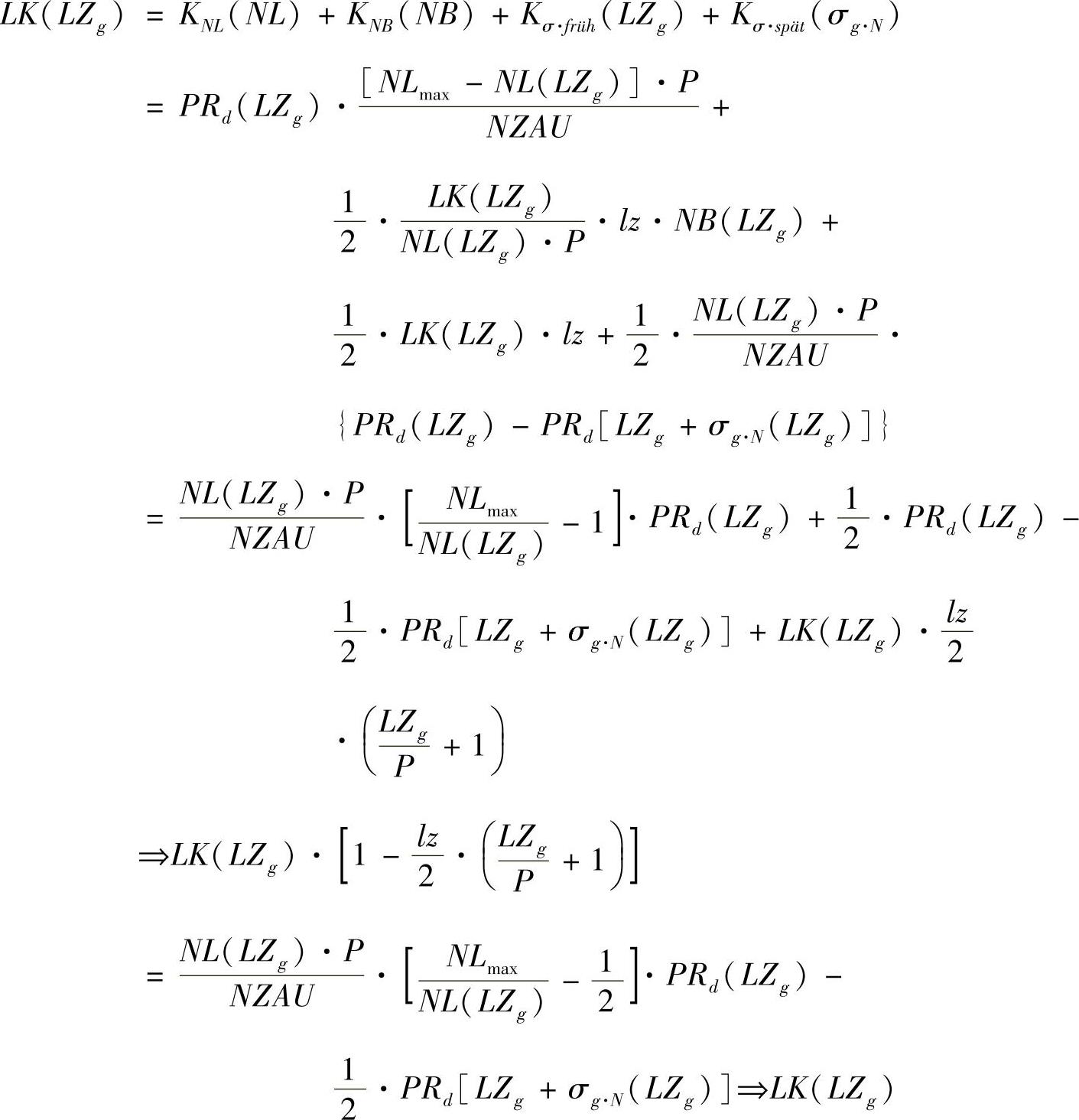
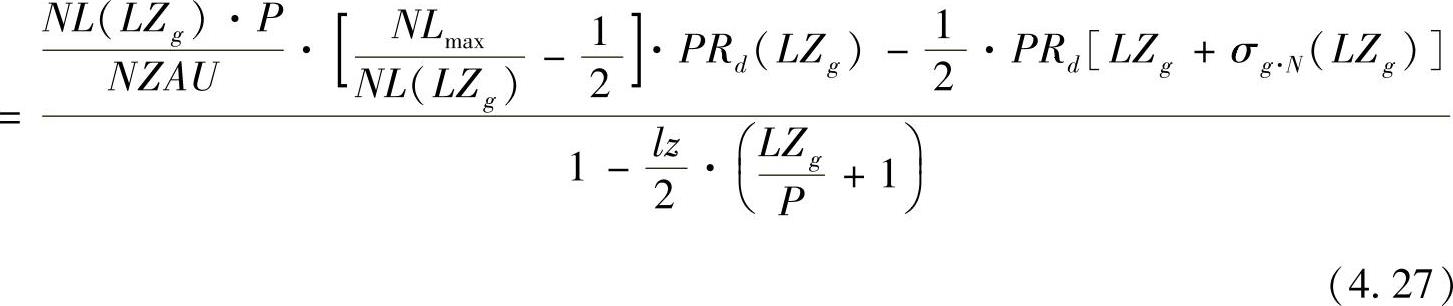
式中 LK——网络中的总供货成本；

LZ_g——被加权的平均供货时间；

K_NL——网络中一次效率下降的成本；

K_NB——网络库存的成本；

K_σ·spät——延迟的订单的成本；

K_σ·früh——提早完成的订单的成本；

NL——总订单时间内的平均网络效率；

NB——总订单时间内的平均网络库存；

σ_g·N——网络中被加权的标准偏离；

PR_d——每个订单的平均价格；

P——计划阶段的长度；

lz——仓储管理利率。

生产网络中的供货成本函数在我们的实例中具有最小值（见图4.8）。

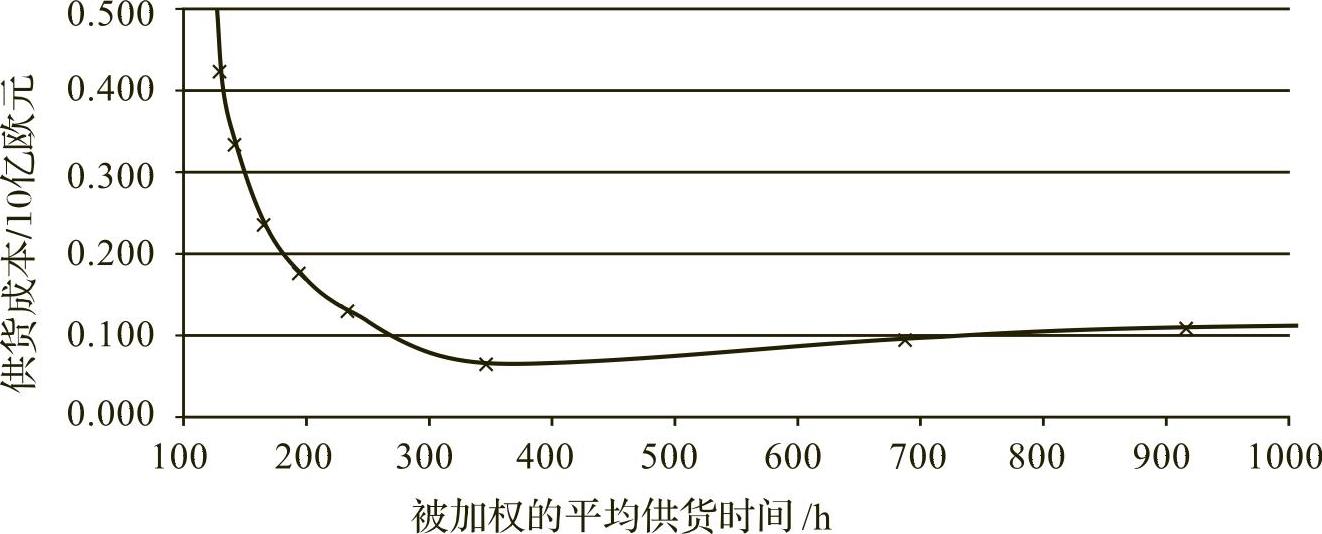
图4.8 实例：网络中的供货成本

来源：作者。