分散生产计划与控制的挑战和解决方案

不同于连续性计划对生产进程中的结构性特征进行准确界定，生产模型在描述动态进程时表现出很大的不足。例如，以平均值的形式来描述进程中的通过时间或库存等过程特征，完全没有考虑这些数值可能发生巨大变化。

尽管如此，生产过程模型的准确性也随着不断向执行层面靠近而日益提高。例如，在二级需求计划中通过时间往往精确到天，而在确定进程期限时则通常精确到小时，甚至分钟。由于实际情况千变万化，连续性计划最迟会在生产需求计划层面遭遇问题。尤其是当不可预测的干扰出现后，耗费巨大制订出的计划往往在几个小时之后就需要被重新制订。这种SAP-APO带来的高度“紧张”一再遭到诟病，而且细小的数据变化就会导致大面积的计划重审，但又仅局限于并发症，并不能从根源上解决问题。

由于集中式的生产需求计划干扰状况频出，能够真正得以实施的计划越来越少，而集中式生产计划和控制应用型欠佳的问题也日益凸显。因而，从20世纪80年代末起，人们越来越多地采用借助MES的PPS分散式模型。不够完善的连续性计划（通常是在ERP系统中）通过分散模式得以补充，这些分散的方式可以在较小的生产领域减少干扰，从而能够更好地反映真实的现状。我们会对看板管理和BOA这两种PPS协同方法进行更具体的阐述，以说明其如何适应一个组织的分散性，或者说一个“内部的网络”。这种适应被看作是在企业网络中采用PPS的前期准备。

由于采用了分散的方法，生产过程被拆分为相互独立的单位，从而可以减小复杂程度，更好地反映现状，并且更快、更准地进行计划和控制，也能在不干扰整体系统的情况下实现本地适应和本地变更。对分过程的调节要求必须做到产品跟踪。与工业4.0密切相关的技术进步确保能够实现更大的经济效率。

PPS分散法可以被视为组织结构上的分散处理。也就是说，之前由某一个主体来执行的PPS行动权（能力），现在至少被部分地分配给了多个主体。能够实现这样的转换，前提需要我们将PPS任务划分为决定权、计划权和信息权。在运用分散法的同时，由于计划和执行之间的区分被部分消除，所以要求更有效的行政工作和参与员工更高的积极性。

PPS分散法是以企业内部的分散的生产架构为出发点的，这些分散的生产构架构成了车间生产或小组生产这一类管理研发和灵活生产体系以及MES这一类技术研发的基础。从法律意义上讲，它们是隶属于一个企业，但却包含多个中心的组织机构。在这里我们可以把由多个工作进程组成的进程组或者由多个工位组成的工作组看作一个单位。这些单位拥有自己的行动权，并形成多个中心（多中心的），这些中心有一部分是多余的，因为它们配备了相似的车间或者工作组，并形成了“内部网络”（参见第2.2.1小节）。我们应该遵循的法则是：系统越复杂，就越有必要实行分散化和自我管理。这一点对于网络中的复杂生产过程尤为适用。

在PPS分散化之初，生产流程计划和数据管理通常仍是集中的。各种理念的不同之处在于如何处理生产需求计划和控制以及订单调节的任务。在这方面出现了三个主要的发展方向。

1）带有分散式生产控制的集中式生产流程计划和生产需求计划，不含订单调节。

2）带有分散式生产控制和集中式订单调节的集中式生产流程计划和生产需求计划。

3）带有分散式生产需求计划和控制以及分散式订单调节的集中式生产流程计划。它对应着分散的个体单位的自控或者以物流为导向的PPS系统。

第一种类型的优势在于，对于企业而言，带有不太细化的生产过程模型的中心个体就能满足需求，因为分散的单位负责完成细化的生产控制。与之相反，各个独立的工作小组则应用更加细化的，但往往固定的模式，这些模式的复杂性自然会受到限制，因此只有相应的工作小组对应的那部分生产领域能够被呈现出来。

集中式计划主体通常需要一个时间缓冲器，以便在遭遇干扰时可以给予权限单位足够的应对空间。我们还应该尽可能地就地解决干扰，避免给中心个体造成额外负担。当然，已完成的订单、获得半成品的节点以及工作环节遭遇的很可能会持续较长时间的干扰都要反馈给中心计划，以便中心计划能够对生产进程进行调整，并通过修改计划来应对干扰。

在这种情况下，中心实体必须接管生产控制任务。订单被视为干扰出现时为操作时限配备的更大的时间缓冲器，从而避免在发生小干扰时就采取集中式的调节措施。由此产生的计划通过时间的延长会导致或者加重通过时间并发症。

此外，依旧很有必要在分散的单位之间和集中的生产进程计划之间进行协同。这使中心个体有可能遭遇瓶颈，因为当分散单位的可接受度被打破之后，除了将启用形式上的权限外，还将启用与问题状况相符的信息接收和处理机制。这不仅要求中心实体具备足够的信息量，还必须同时具备相应的信息处理能力。随着PPS越来越复杂，中心个体也需要不断得以加强，并且要针对不同的问题状况有所区分和专业化。正如阿什比提出的必要差异定律所要求的那样，一个具有复杂性的体系只有依靠同样复杂的一个体系来加以控制。这将导致在被称为“冯·纽曼瓶颈”的集中层面对原本分散的协同问题进行再生产。

第二类型中的集中式订单调节被很多作者认为最为理想。这种订单调节的首要任务是，将中心计划主体从对分散单位的协同工作中解脱出来，并在干扰发生时根据具体情况采取干预性调节。在这种情况下，订单调节阶段性地从中心主体那里承担了有大致时间期限的订单，并把它们分配给分散的单位。在遭遇产生重大后果的干扰时，订单调节系统会接收到反馈，并采取必要的应对措施。订单完成之后，完成信息也会被传送给中心主体。这样可以防止中心主体受到生产过程中意外状况的负面影响。尽管如此，仍然为操作时限保留了时间缓冲器，而且订单调节在确保各个独立单位目标一致性的过程中仍然有可能遭遇瓶颈。此外，在这种类型中，对于中心订单协同而言，协同问题也被重新定位为次重要的、对分散单位进行协同的主体。

在第三种以供应为导向的模式中（见表2.3），生产需求计划是以分散形式进行的，而不像前两种模式那样依靠居高的一个调节主体来进行。这种依然保持集中的生产流程计划也可以允许兼容不同的分散方式，主要取决于相应的生产过程具备什么样的应用前提。分散式的PPS模型有：20世纪80年代就开始被应用的看板管理，以及以负荷为导向的订单投放（BOA）。利用流水线原理进行生产的领域或企业可以以看板系统的方式进行分散式控制，而其他进行车间生产的领域或企业则往往采用BOA的分散式控制。当然，这些分散式控制可以根据各局部的控制理念在生产流程控制这一大框架中被联合应用。

表2.3 对比传统PPS和以供应为导向的PPS提出的要求

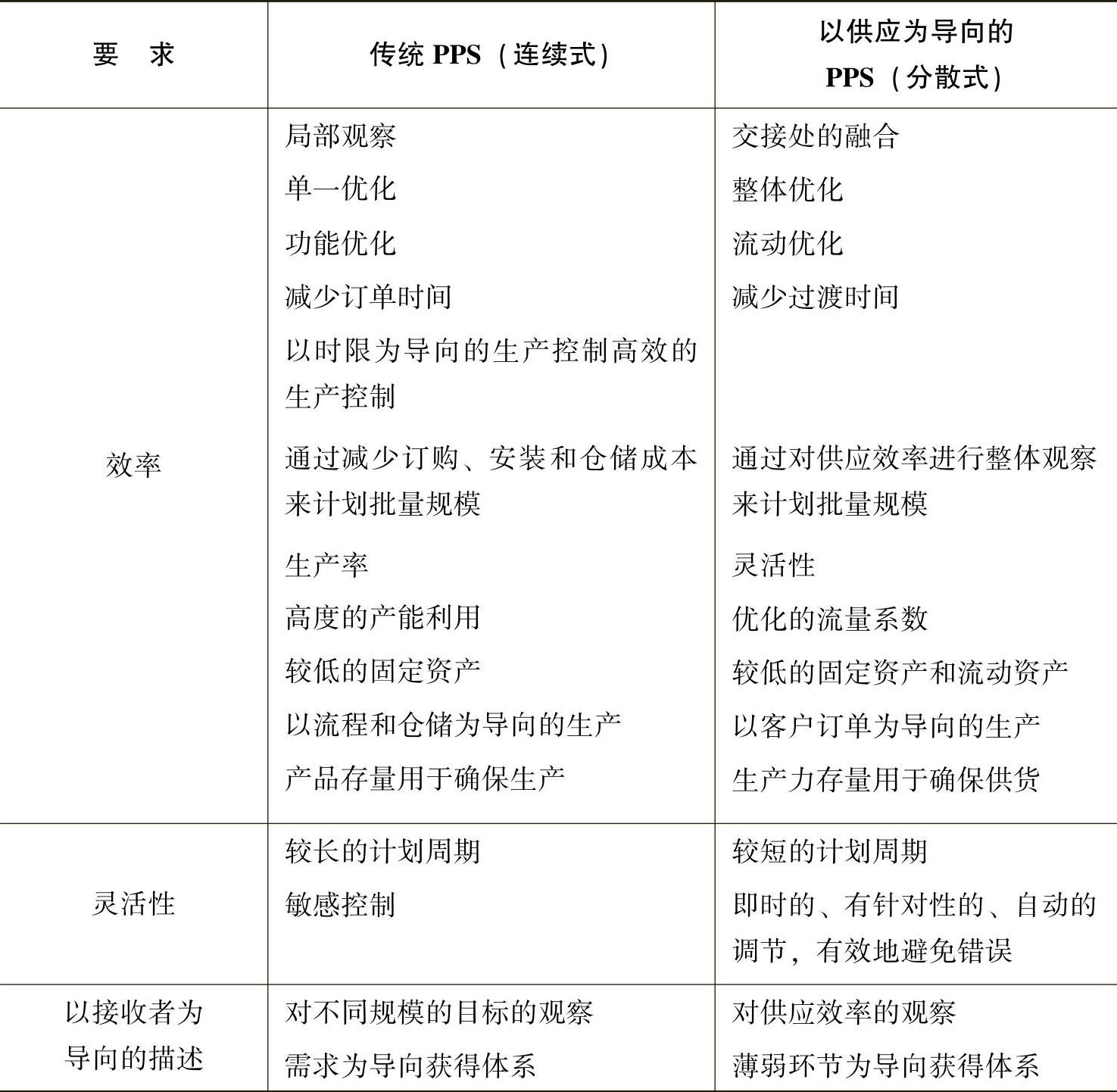
来源：斯图加特大学企业经济促进会，1988，第75页；Eidenmüller，1985，第182页；Lucke等人，1990，第120页；Bichler等人，1992，第4页及下页；Delfmann，1995，第511页；Vahrenkamp，1996，第65页及之后数页。

各单位的自控和各单位之间的沟通可以分为几种不同的类型：

• 在最简单的类型中，分散的单位会从负责制订生产流程计划的中心主体处得到订单，这些单位也会知晓各生产领域的分过程，从而可以估计自己的行为给其他领域造成的影响。

• 在高级类型中，各单位之间则可以进行明确的沟通，并以这种方式在遭遇干扰时在上级协同者限定的范围内协商应对措施。

• 除了上述两种类型以外，还有另外一种补充类型。在这种补充类型中，各单位之间以合作的方式来完成生产需求计划和控制，中心主体只根据生产流程计划或者既有订单制订交货日期。各个分散的单位将对它们的计划与其他各领域和采购进行协同。

从与工业4.0相关的技术的实践性来看，上述第三种类型是最理想的一种选择。下文将对看板管理和BOA两种方法进行研究，也是以第三种类型为基础的。我们将对它与集中式生产流程计划在目标上的一致性进行探讨，同时还包括对效率和透明的生产跟踪的探讨。

看板管理由大野耐一（原丰田汽车制造厂副总裁）提出，并最初在日本丰田汽车制造厂得以利用。这一体系区别于其他体系的地方在于，它的生产控制框架里并没有对将来的计划。看板管理在生产控制中完全采用的是依据延性原则的反应式方法，即工作系统中的消费者根据需求来从相应的库存中获取物料和产品。

生产者借助一个与物料容器相连的电子的或者纸质的卡板（日语为“看板”），在消费者获取物料之时就得到通知。生产者紧接着生产出相应数量的产品，并将仓库库存补充至原始状态。

在生产需求计划阶段，中心主体会为每一个生产阶段确定库存和生产力需求。不管处于哪一个加工过程，都需要建立自己的仓库。而在传统的生产需求计划中，因为要耗费大量的物力和进行组织管理，只有在进行耗时较长的生产时才会考虑建立自己的仓库。因为和生产控制中需要遵守的流程规则联系在一起，生产需求计划中的结果的有效时限往往比在其他PPS体系中更长。这里涉及的并非一种以供应为导向的类型。

出于上述原因，看板管理的应用需要具备一定的前提条件：

• 没有差异的标准产品或者只带有生产商特供差异型号的标准产品。

• 以框架订单为基础的客户订单或者销售计划相对稳定的仓库订单。

• 产能负荷相同的大批量生产（容量截面协同）。

• 流水线生产或者成组生产。

• 较少的生产过程，以使生产需求计划的耗费尽可能低。

这一系统在看板管理中心需求计划中被激活，也就是说，相应的生产领域被划分为独立的工作体系，这些体系既扮演消费者的角色，又扮演生产者的角色。而一个工作体系可以是一个独立的工作岗位、一个工作小组、一个控制领域、整个企业或者包括缓冲存货的整个企业网络。缓冲存货的安置可以使各个工作岗位相互分离开来。

缓冲存货是由带有恒定填充量的标准容器构成的，每个容器上都配有一张卡片，卡片上标明了容器的种类及其标准填充量等。缓冲存货规定值的计算来自容器的数量或者看板卡片的数量以及每个容器的填充量。在确定这个中心数值时，平均周期时长和缓冲存货再次补给时长有着相当重要的意义，其中缓冲存货再次补给是通过生产体系自行生产或者从供应商处采购来完成的。周期时长可以通过与客户和供应商签订的框架协定或者生产流程计划来确定。这些部分的首次生产以及缓冲存货的发送都是通过应有存量在系统激活中完成的。

分散式的生产控制（系统运行）以流程调节为特征，它要能够在较低库存的情况下保证持续的物料流：

• 只有具备了看板卡片形式的订单之后，生产系统才可以进行生产。

• 生产系统必须严格按照看板卡片上规定的数量进行生产。

• 生产系统只能按照实际所需，从缓冲存货中获取装有部件的容器。

看板管理的一个优势在于它的系统运行非常简单，能让我们不再需要生产控制中的中心订单调节。看板管理的运行不需要计算机支持就充分证明了这一点。这一体系相对于生产过程中的短期干扰所具备的抵御能力也相对较高，一方面因为生产系统被缓冲器隔离开来，另一方面因为各个加工过程的起始和终止时间并不是简单地由计划过程来决定的，而是根据需求状况得到的。只要能够很好地遵守系统运行中的流程规则，就能通过循环着的看板卡片的数量和容器填充量来限制生产库存的数量。

与之相反，系统激活则是以集中方式进行的，并且不包含对系统运行进行连续监控得到的反馈。当需求临时出现变化或者产品组合发生改变时，看板管理的灵活性相对较弱，因为对于每一个生产阶段遇到的变化都必须要建立或补充缓冲存货。生产商面对临时增加的需求，可能无法做到准时交货，消费者也可能无法按预期享用产品。如果变量比较大，带有可预见的缓冲存货的生产过程很多，应该从数量上保留较多的库存。

在这种所谓适应性的看板管理体系中，我们可以通过对缓冲填充度的控制和生产人员现场对错误发生量进行登记来得到反馈，从而使调控中心或者中心订单调节了解到超出或未达到临界值的情况。调控中心可以通过取出或填补看板卡片来满足应有的缓冲量。只有通过这种延伸方式，看板管理方法才能够应对较大的需求变化。中心订单调节则仅会导致调节问题的拖延。

正如订单调节一样，集中的数据管理也仅对系统激活有必要。在适应性的看板管理方法中，企业会实时更新数据管理所需要的数据库，并把较大的变化情况反映给订单调节。

以负荷为导向的订单放行法（BOA）在企业经济学中虽然引起了较为广泛的讨论，但相对于看板管理，它也受到了不少批评之声。它以所谓的漏斗模型为基础，是一个以统计为导向的PPS方式。在这种方式中我们会考虑并不能准确预计的、根据统计得来的停工时间对通过时间造成的重大影响。漏斗模式对生产过程提供了一种完全可以标准化的、又不太复杂的描述方式。借助这种方式，我们一方面可以结合企业结构来表现订单的开展行为，另一方面也可以描述生产目标规模之间的现有关系，从而让我们有可能借助标准化的方式及时来构建一个不受企业类型影响的过程模型。

漏斗对应着一种生产系统。在一个订单i到达一个生产系统的那一刻（进入），等待着的订单就形成了状态B_i，并在加工之后流出漏斗（离开）。漏斗开启意味着效率L_i，即每个单位时间内离开的订单。不断变化的漏斗开启状况说明，它的效率随着可用的产能发生变化，也就是说最终代表着可用产能。

如果我们设定所有订单依照它们进入漏斗的先后顺序被处理（FIFO规则），那么依据漏斗模型，完成一个订单i的时间Z_i就应该为

式中 Z_i——订单的通过时间；

B_i——在订单i到达时，生产系统面前等待的订单状况；(www.xing528.com)

L_i——在订单i达到时，用单位时间内离开的订单量来表示的生产系统的效率。

这表明，我们可以通过对某一生产系统的订单量进行调节来影响通过时间。进入生产系统的状态影响了订单存量的多少，继而影响了生产系统的通过时间。

一个订单i在生产系统中的通过时间Z_i来自于加工时间、安装时间、加工之后需要存放的时间、运输和运输后需要存放的时间以及通常所说的过渡时间。将要被完成的工作称为订单时间ZAU_i，这一时间由订单i在工作系统中的加工时间和安装时间构成。状态B_i可以被看作是订单在某一时刻等待进入生产系统的时间。上述规律也同样适用于将要被完成的工作，即效率L_i。

所有在式（2.1）中出现的数值其实都是时间段，它们能够为所有的生产系统提供可描述的、可标准化的、清晰的过程段，同时还能为生产提供漏斗模型中完整的可结合性和可分拆性，从而可以借助订单时间把生产系统中各不相同的等待中的订单用时间单位聚合起来。在这个过程中，我们也可以不用式（2.1）中的跟订单相连的数值，而直接使用平均值。“漏斗公式”对此进行了如下描述

式中 MZ_g——生产系统中订单的平均通过时间；

MB——用订单时间来表示的生产系统中订单的平均存量；

ML——生产系统中的平均效率。

这种将平均存量和平均效率做比得到平均通过时间的算法被称作漏斗公式。在式（2.2）中，计划时段的长度并不是被订单的数量所平均，而是被通过生产系统的、用小时来计算的工作所平均。而生产系统中的平均通过时间MZ_e，也就是平均来看，一个订单在生产系统中停留的时间，可通过下列公式计算得到

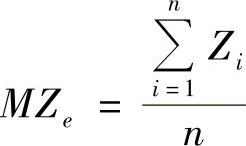
式中 n——订单的数量；

Z_i——订单i的通过时间。

MZ_g表示的是一个工作单位在被观察的生产系统中完成订单（如1h）平均需要多少时间。这个计算对许多不同的订单进行了对比，从而得到了一个平均值。平均通过时间被定义为

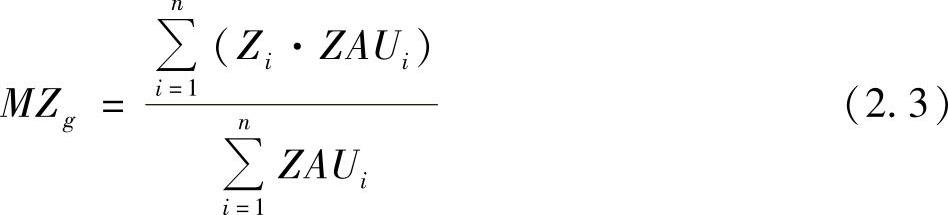
式中 MZ_g——平均通过时间；

Z_i——订单i的通过时间；

ZAU_i——订单i的订单时间；

n——一个计划区间内的订单数量。

应用漏斗公式以及BOA必须要满足下列前提条件：

• 存量——效率比率保持不变；在计划时段中因为顺序调换而相互抵消的长度P的影响。Nyhuis和Wiendahl没有选择平均通过时间，而选择了平均有效范围来表述漏斗公式。在我们所说的应用前提下，平均有效范围即指平均通过时间。

• 每个订单时间已知的加工和安装时间都有相同的增加值。这些约束条件尤其适用于BOA的批量计划。

• 在小批量情况下进行与订单相关的、受需求控制的生产可以满足客户提出的改变。应用这一方式的基础是，必须计算出每个单个订单的订单时间ZAU_i。如果是在以消耗为导向的控制中，由于加工和安装时间起到的控制作用较小，计算订单时间则是不必要的浪费，因为对于某一个产品变量来说订单时间是固定不变的。而为客户量身定制的单一生产则与“平均”过程进度相距太远，以致BOA这一统计学方式无法对其提供有效的说明。不过依据与订单有关的、以需求为导向的生产也可以断定，单一生产的产品具有较高价值，或者说其价值与存量的成本相符。

• 车间生产或者灵活的生产系统带有间断性原料运输或者等待进入下一加工阶段的不同批量大小的半成品，因此有必要配置中间存货。

因而，BOA这种系统非常适用于带有不断变化的客户订单和生产变量的生产领域。

BOA以固定产能为出发点，这个固定产能是在集中式生产流程计划中经历了较长的时间以及产能的密集阶段（如对于整个生产运行而言）才被确定的。为了把生产流程计划层面的产能计划和生产需求和控制层面的产能需求结合起来，BOA系统制订了一个产能计划，当发生改变的分类计划遇到被改变的订单集合时，产能计划就会做出反应。

集中式的BOA生产需求计划被划分为批量大小计划和期限及机器占用率计划。

BOA的批量大小计划以批量加工和为被观察的生产系统提供的批量运输为出发点，它的目标在于，在产能消耗连续的前提下，实现库存最小化。因此我们相应地把待测算的平均批量看作是一段订单时间内所必需的平均最小存量MB_min，这一最小存量可以使得生产系统上始终至少保留一条订单，从而保证生产系统的持续产能消耗。每次超出MB_min的存量减少或者批量规模减小都可能导致生产系统上暂时没有订单。

我们借助MB_min不仅考虑到了订单时间的平均值MZAU，同时也考虑到了它以订单时间的标准偏离σ_ZAU形式进行的控制：

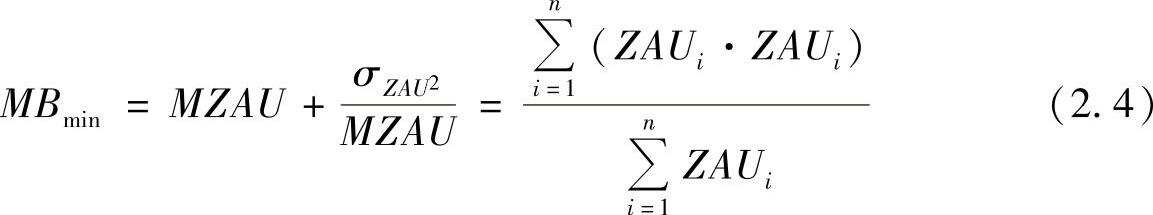
式中 MB_min——订单时间内的平均最小存量；

σ_ZAU——订单时间的标准偏离；

n——一个计划时段内的订单数量。

要制订时限和机器占用率计划必须先确定平均通过时间。Wiendahl认为，可以借助生产特征曲线来计算这一数值。生产特征曲线既描述了通过时间和效率这两个PPS参数理想化的、确定的变化过程，也描述了其接近真实的、通过近似方程式得到的变化过程。

在计划时段P中，我们为不同生产系统的不同平均存量和不同平均效率制订了相应的平均通过时间MZ_g。当MB＜MB_min时，表示物料流发生减少，而在拐点MB=MB_min时则会出现较大的效率下滑。当MB＞MB_min时，效率特征曲线ML非常接近可支配的产能。这时，很可能由于在到达过程中对最小过渡时间以及产能需求和产能供应之间的差异进行的控制而使实际值与理论上的拐点有细小差别。

通过上述效率特征曲线的变化和式（2.4）可以得出，平均订单时间及其控制通过MB_min来确定平均通过时间、平均存量和平均效率的特征曲线的拐点状态，当处于拐点之上时，不会发生大的变化。

Wiendahl认为，如果要在尽可能大的负荷下，即在拐点之后进行生产，必须将尽可能小的通过时间和尽可能小的存量作为第二要务。最小的通过时间和MB＞MB_min时的最小存量会在拐点出现，即当MB=MB_min时。所以计划所要获取的“最佳系统状态”即是特征曲线的拐点。在这一系统状态下，我们通过特征曲线既规定了计划效率和试图达到的平均存量（计划—存量），又规定了试图达到的平均通过时间（计划—通过时间）。

在我们借助生产特征曲线及其拐点确认了计划—通过时间之后，即可借助逆向定时和由计划存量决定的时间表，以及通过对产能负荷统计计算来实施期限计划和机器占用率计划。逆向定时的依据是供货期限和工作岗位通过时间。我们通过逆向定时可以计算出生产起始日期，并同时估算出平均通过时间。时间表会确定出我们在生产需求计划的后续进程中会对哪些订单进行观察。Wiendahl认为，这些被观察的订单的生产起始日期应该在接下来的第一至第三个计划段内。通过产能负荷我们还可以了解到某个订单有多大可能性在紧接着的阶段达到工作岗位（如果它之前还有其他工作岗位需要通过的话）。

只有当没有任何一个工作岗位发生负荷箱被超出的状况时，订单才能够被放行。它通常是用百分比表示的计划阶段中可被利用的产能的倍数。

“通过负荷箱我们可以确保，不论订单到达哪个工作岗位，它都能找到与计划通过时间相符的存量状态。”

负荷箱是BOA系统中的中心参数。BOA系统对生产控制做出了如下规定，即在订单放行之后，车间人员必须立即确定订单加工的顺序，车间人员在此过程中遵循的类似于其他PPS方式中的优先原则使其相对偶然性原则或者FIFO系统更加准时地完成交货。

我们并不对单个的生产过程准确规定起止日期，而是结合有可能遵循的优先性原则仅确定生产订单的放行时间。通过现场员工的决定权可以消除干扰，这样的做法也得到了高度认可。

在BOA系统中，订单调节可以分散地以“生产领域的控制系统”的形式来实现。顺沿生产流程的订单监管（水平的）和一个生产系统的监管（垂直的）都是以分散的方式，即与生产系统相关的方式展开的。所有得到的数值可以通过标准化的流程个体适用于整个生产运行。在所有聚合层面上，我们都可以利用生产特征曲线图来检验这些数值是否满足PPS系统制订的目标。基于此，各种不同规模的分散的单位都可以进行自检，并了解到与自身相连的前后工作系统的状况，以便在生产控制层面对有可能出现的干扰做出应对。当然，如何应对无法提前预知。

通过对生产系统进行监测，我们也有可能以集中的方式利用重新计划来应对生产过程中出现的干扰。但是我们并不提倡生产系统之间的明确沟通或者合作性的、分散的生产需求计划和控制。

BOA的数据管理是以具备一些所谓的结构数据和框架数据为前提的，我们在表2.4中列举出了这些数据。工作岗位团组被视为相似的工作岗位的集合，它们之间可以发生短期的人员交换。

表2.4 BOA中的结构数据和框架数据

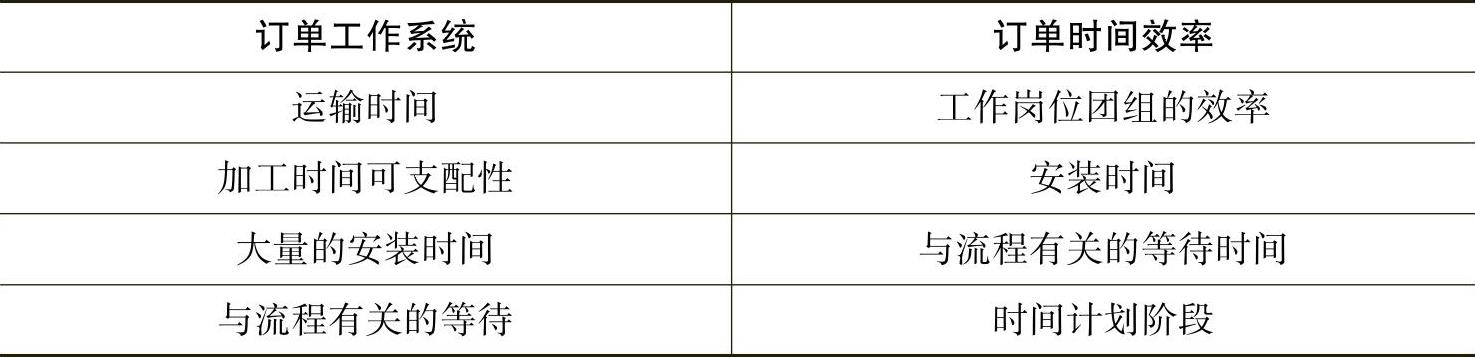
来源：Wedemeyer，1989，第17页和99页；Schulte，物流——通向物料流和信息流优化之路，第3版，1999，第284页。