中国分税制模型的识别方法

（1）对数线性化模型

根据本章5.1的分析，对DSGE模型的识别首先需要对模型进行对数线性化。

家庭部门的对数线性化结果为：

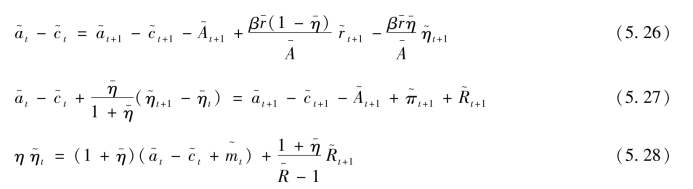
生产厂商的对数线性化结果为：

市场出清和政府预算平衡的对数线性化结果：

接下来，对经济系统中货币政策和外生冲击方程进行对数线性化，其结果为：

(www.xing528.com)

至此，所有部门的非线性方程通过对数线性化技术转变为线性动态方程。即式（5.25）—（5.42）共同构成线性化系统，接下来，可以针对对数线性化系统做出模型识别的分析。

（2）模型识别

在本书中，选取的可观测变量为国内生产总值（GDP）、社会消费品零售总额、就业人数、消费者物价指数（CPI）、货币供给量（M2）、货币余额，按照Ivana＆Serena（2011）规定方法，即ny＝6。显然，模型中包含7个随机的外生冲击，并且假定所有外生冲击不相关，即nε＝7，∑ε为对角矩阵。显然，nε＞ny，该DSGE模型是非奇异的。并且，在无约束的情况下，待估的结构参数的个数为20。由于选取了6个可观测变量，此时不可观测的状态变量的个数即为nξ＝14。根据命题5.1.2，可以验证，在无约束的情况下，nθ＞2nξny+ny（ny+）1／2，即该非奇异的DSGE模型在无约束的情况下不满足命题5.1.2的阶条件，因此，该模型不可识别。

根据本章5.2的分析，可以采用参数校准的方法确定部分结构参数，即将参数校准看作是对结构参数施加的严格的点约束。不妨设需要校准的参数个数为nc，则待估的结构参数个数为20-nc，根据命题5.1.2的阶条件可知，若该DSGE模型可识别，必须满足≤2nξny+ny（ny+）1／2＝189，则必然有nc≥7，即至少需要校准7个结构参数。

（3）参数校准

在本书中稳态参数的校准值通过两种途径获得：一种是利用实际宏观经济数据^[7]通过稳态方程推算得出，另一种是结合相关文献的惯例得出。本书总共校准了9个参数，满足了上述模型可识别的阶条件，并且在运用Dynare工具包对模型动态参数进行Bayes分析以及随后的模拟分析中，均得到了稳定的结果。

季度存款利率由1990年至2013年的一年期存款基准利率计算得出，进而得到季度贴现因子β的校准值为0.982。根据刘斌（2008）、张杰平（2012）等人的文献，将劳动产出份额λ校准为0.6，则资本产出份额1-λ为0.4；此外，参考多数学者的研究以及根据我们的模拟试验结果，反映价格粘性程度的参数φ校准为20，劳动供给弹性的倒数ξ校准为2，季度资本折旧率δ校准为0.0258。另外，借鉴刘斌（2008）对于泰勒规则中各参数的设定方式：设定产品需求替代弹性θ为8，名义利率弹性ρR为0.95，通货膨胀率弹性ρπ校准为0.7，产出弹性ρy校准为0.5。稳态时各参数的校准值如表5.1所示。

表5.1　稳态参数校准值

续表